Pythagorean identitet Demonstrasjon, eksempel, øvelser

Er Pythagorean identiteter Alle trigonometriske ligninger som er oppfylt for enhver verdi av vinkelen og er basert på Pythagoras teorem. Den mest kjente av Pythagorean -identiteter er den grunnleggende trigonometriske identiteten:

Sen²(α) + cos²(α) = 1

Figur 1. Pythagorean trigonometriske identiteter.

Det er fremdeles i betydning og bruker den pytagoreiske identiteten til tangenten og secant:

Så²(α) + 1 = sek²(α)

Og den pytagoreiske trigonometriske identiteten som involverer Cotangent og Harvester:

1 + CTG²(α) = CSC²(α)

[TOC]

Demonstrasjon

De trigonometriske grunnene bryst og kosinus De er representert i en radiusomkrets en (1) kjent som trigonometrisk sirkel. Denne sirkelen har et senter ved opprinnelsen til koordinater eller.

Vinklene måles fra den positive semi -aksen til X, for eksempel vinkelen α i figur 2 (se senere). I motsetning til klokkehendene hvis vinkelen er positiv, og i retning av hendene hvis det er en negativ vinkel.

Semi -rett med opprinnelse eller og vinkel α er trukket, noe som avskjærer enhetssirkelen ved punkt P. Punkt P er projisert ortogonalt på den horisontale aksen X som gir opphav til punkt C. Tilsvarende er P projisert vinkelrett på den vertikale aksen og gir opphav til punkt S.

Du har riktig OCP -trekant i C. 

Brystet og kosinus

Det må huskes at trigonometrisk grunn bryst Det er definert på en høyre trekant som følger:

Bosomen til en vinkel på trekanten er forholdet eller forholdet mellom katetoet i motsetning til vinkelen og hypotenusen til trekanten.

Anvendt på OCP -trekanten i figur 2 ville være slik:

Sin (α) = cp / op

Men CP = OS og OP = 1, slik at:

Sin (α) = OS

Noe som betyr at projeksjonen på Y -aksen har en verdi som er lik barmens vinkel vinkel. Det skal bemerkes at den maksimale verdien av brystet i en vinkel (+1) oppstår når α = 90º og minimum (-1) når α = -90º eller α = 270º.

Kan tjene deg: Vektorrom: base og dimensjon, aksiomer, egenskaper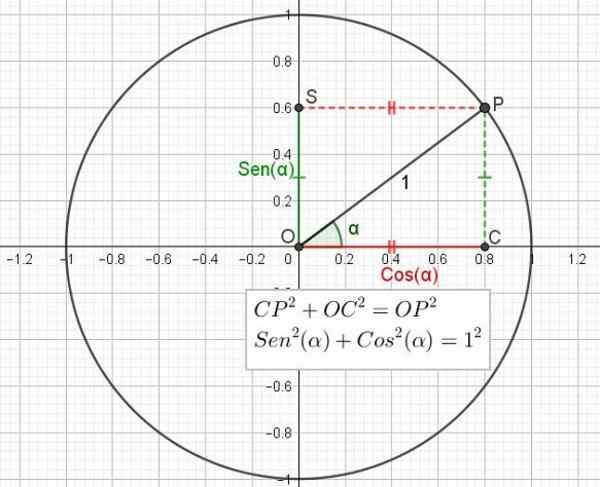Figur 2. Trigonometrisk sirkel som viser forholdet mellom Pythagoras teorem og grunnleggende trigonometrisk identitet. (Egen utdyping)

Tilsvarende er kosinus i en vinkel forholdet mellom kategorien ved siden av vinkelen og hypotenusen til trekanten.

Anvendt på OCP -trekanten i figur 2 ville være slik:

Cos (α) = oc / op

Men OP = 1, slik at:

Cos (α) = oc

Noe som betyr at OC -projeksjonen på x -aksen har en verdi som tilsvarer den for vistet vinkel. Det skal bemerkes at den maksimale verdien av kosinus (+1) oppstår når α = 0º eller α = 360º, mens minimumsverdien til kosinus er (-1) når α = 180º.

Den grunnleggende identiteten

For rectangle OCP -trekanten blir Pythagoras -teorem brukt, som sier at summen av kvadratet til kategoriene er lik kvadratet til hypotenusen:

CP² + OC² = Op²

Men det er allerede blitt sagt at CP = OS = sin (α), at OC = cos (α) og at op = 1, slik at det forrige uttrykket kan skrives om avhengig av sinus og kosinus i vinkelen:

Sen²(α) + cos²(α) = 1

Tangensaksen

Akkurat som x -aksen i den trigonometriske sirkelen er kosinasaksen og aksen og brystets akse, på samme måte er det aksen til tangenten (se figur 3) som er nettopp linjen tangent til enheten Sirkel på punktet på punkt B -koordinaten (1, 0). 

Hvis du vil vite verdien av tangenten til en vinkel, trekkes vinkelen fra den positive halvakselen til X, skjæringspunktet i vinkelen med tangentens akse q, lengden på OQ -segmentet er tangenten i vinkelen.

Kan tjene deg: algebraiske derivater

Dette fordi per definisjon er tangenten til vinkel α den motsatte kateto qb mellom den tilstøtende katetten OB. Det vil si det (α) = qb / ob = qb / 1 = qb.

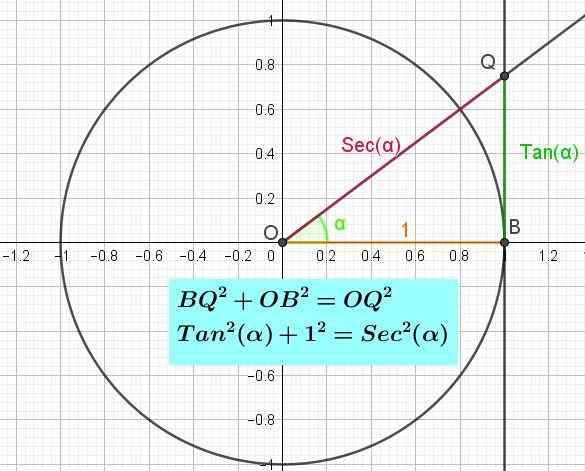Figur 3. Den trigonometriske sirkelen som viser tangentens akse og den pytagoreiske identiteten til tangenten. (Egen utdyping)

Pythagorean identiteten til tangenten

Den pytagoreiske identiteten til tangenten kan demonstreres hvis rektangelets trekant i B (figur 3) er vurdert (figur 3). Bruke Pythagoras -teoremet til nevnte trekant du må BQ² + Ob² = OQ². Men det er allerede blitt sagt at BQ = Tan (α), at OB = 1 og at OQ = sek (α), slik at utskifting i likheten av Pythagoras for høyre trekant OBQ har det:

Så²(α) + 1 = sek²(α).

Eksempel

Kontroller om pytagoreiske identiteter er oppfylt i rektangelet Triangle of Catetos AB = 4 og BC = 3.

Løsning: Kategoriene er kjent, det er nødvendig å bestemme hypotenusen, som er:

AC = √ (AB^2 + BC^2) = √ (4^2 + 3^2) = √ (16 + 9) = √ (25) = 5.

Vinkelen ∡bac vil bli kalt α, ∡bac = α. Nå bestemmes de trigonometriske årsakene:

Sin α = bc / ac = 3/5 

Cos α = ab / ac = 4/5 

Solbrun α = bc / ab = 3/4 

Cotan α = ab / bc = 4/3 

SEC α = AC / AB = 5/4 

CSC α = AC / BC = 5/3

Det begynner med grunnleggende trigonometrisk identitet:

Sen²(α) + cos²(α) = 1

(3/5)^2 + (4/5)^2 = 9/25 + 16/25 = (9 +16)/25 = 25/25 = 1

Det konkluderes med at det er oppfylt.

- Den neste pytagoreiske identiteten er tangenten:

Så²(α) + 1 = sek²(α)

(3/4)^2 + 1 = 9/16 + 16/16 = (9 + 16)/16 = 25/16 = (5/4)^2

Og det konkluderes med at identiteten til tangenten er bekreftet.

- Tilsvarende det av cotangenten:

Kan tjene deg: tilfeldige valg med eller uten erstatning

1 + CTG²(α) = CSC²(α)

1+ (4/3)^2 = 1 + 16/9 = 25/9 = (5/3)^2

Det konkluderes med at det også er oppfylt, som har fullført oppgaven med å verifisere de pytagoreiske identitetene for den gitte trekanten.

Løste øvelser

Test følgende identiteter, basert på definisjonene av trigonometriske årsaker og pytagoriske identiteter.

Oppgave 1

Bevis hva Cos² x = (1 + sen x) (1 - sin x).

Løsning: Høyre medlem gjenkjenner det bemerkelsesverdige produktet av multiplikasjonen av en binomial av dets konjugat som, som kjent, er en forskjell i firkanter:

Cos² x = 1² - Sen² x

Deretter passerer begrepet med bryst på høyre side til venstre med det endrede tegnet:

Cos² X + sen² x = 1

Bemerker at den grunnleggende trigonometriske identiteten er nådd, så det konkluderes med at det gitte uttrykket er en identitet, det vil si at det er oppfylt for enhver verdi av x.

Oppgave 2

Starter fra den grunnleggende trigonometriske identiteten og bruker definisjonene av trigonometriske grunner til å demonstrere den pytagoreiske identiteten til Harvester.

Løsning: Den grunnleggende identiteten er:

Sen²(x) + cos²(x) = 1

Begge medlemmene er delt mellom Sen²(x) Og nevneren er distribuert i det første medlemmet:

Sen²(x)/synd²(x) + cos²(x)/synd²(x) = 1/sen²(x)

Det er forenklet:

1 + (cos (x)/sen (x))^2 = (1/sin (x))^2

Cos (x)/sin (x) = cotan (x) er en identitet (ikke -pythagorean) som er bekreftet av definisjonen av trigonometriske grunner. På samme måte oppstår det med følgende identitet: 1/sin (x) = CSC (x).

Endelig må du:

1 + CTG²(x) = CSC²(x)

Referanser

1. Baldor J. (1973). Flat geometri og rom med en introduksjon til trigonometri. Sentralamerikansk kulturell. C.TIL.
2. C. OG. TIL. (2003). Geometrielementer: med øvelser og kompassgeometri. University of Medellin.
3. Campos, f., Cerecedo, f. J. (2014). Matematikk 2. Patria redaksjonell gruppe.
4. Iger. (s.F.). Matematikk første semester Tacaná. Iger.
5. JR. Geometri. (2014). Polygoner. Lulu Press, Inc.
6. Miller, Heeren, & Hornsby. (2006). Matematikk: Resonnement og applikasjoner (tiende utgave). Pearson Education.
7. Patiño, m. (2006). Matematikk 5. Redaksjonell progreso.
8. Wikipedia. Trigonometri -identiteter og formler. Gjenopprettet fra: er.Wikipedia.com