Multiplikativ omvendt forklaring, eksempler, øvelser løst
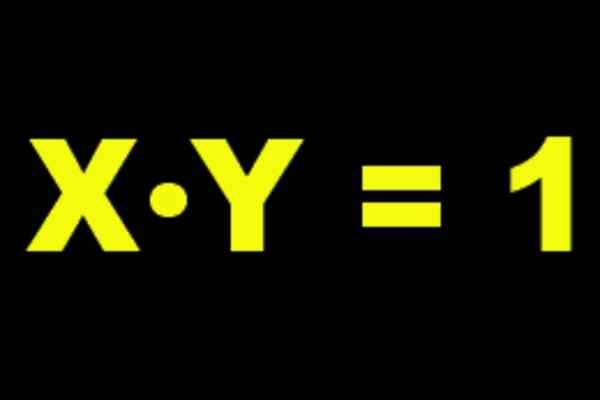
- 3047
- 154
- Prof. Joakim Johansen
Det forstås av Inverse multiplikative av ett tall resulterer et annet tall som multiplisert med det første i det nøytrale elementet i produktet, det vil si enheten. Hvis du har et reelt tall til da betegnes hans multiplikative inverse til-1, Og det er oppfylt det:
a a-1 = a-1 A = 1
Vanligvis tallet til Det tilhører settet med reelle tall.
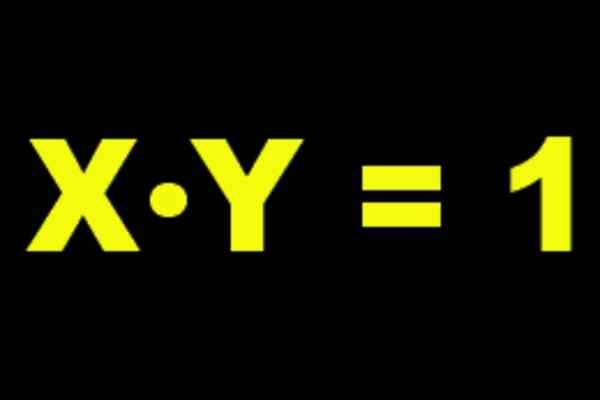 Figur 1. Og det er omvendt multiplikativ av x og x er en multiplikativ inverse av y.
Figur 1. Og det er omvendt multiplikativ av x og x er en multiplikativ inverse av y. Hvis vi for eksempel tar A = 2, Da er din multiplikative inverse 2-1 = ½ Siden følgende er bekreftet:
2 ⋅ 2-1 = 2-1⋅ 2 = 1
2⋅ ½ = ½ ⋅ 2 = 1
Til Inverse multiplikative av et tall kalles også gjensidig, Fordi den multiplikative inverse oppnås ved å utveksle teller og nevner, for eksempel er den multiplikative inverse på 3/4 4/3.
Som en generell regel kan det sies at for et rasjonelt antall (P/q) Din multiplikative inverse (P/Q)-1 Det er gjensidig (Q/P) Som det kan bekreftes nedenfor:
(P/Q) ⋅ (P/Q)-1 = (p/q) ⋅ (q/p) = (p⋅ q)/(q⋅ p) = (p⋅ q)/(p⋅ q) = 1
Det multiplikative inverse eksisterer ikke i det numeriske settet med heltallene, For eksempel, hvis hele nummer 2 er tatt, ville dets multiplikative inverse i henhold til det som ble sett ovenfor være ½, men en ½ er ikke et heltall.
Det er også det multiplikative inverse av nullelementet i multiplikasjon. Med andre ord, nulltallet (0), som er nullelementet i multiplikasjonsoperasjonen, har ikke multiplikativ inverse, siden det ikke er noe tall som multiplisert med null av enheten.
Multiplikativ inverse eksisterer i rasjonelle antall, i reelle antall og komplekse tall.
Multiplikative inverse eksempler
Eksempel 1
Finn 3/2 multiplikative inverse og bekreft at den oppfyller eiendommen til multiplikative heltall.
Kan tjene deg: Coplanares Points: Ligning, eksempel og løste øvelserI henhold til regelen gitt ovenfor, er den multiplikative inverse av (3/2) (2/3) utvekslet på denne måten. For å bekrefte multiplikasjonen av de to tallene utføres:
(3/2) ⋅ (2/3) = (3 ⋅ 2)/(2 ⋅ 3) = 6/6 = 1.
For å multiplisere to brøknummer, multipliser du bare telleren til den første med den andre telleren for å få resultatet Numerator.
For å skaffe nevner av et produkt av brøkdemper, fortsett på en lignende måte, det vil si at nevnerne multipliseres med hverandre, og resultatet er produktnevneren. I vårt eksempel er det bekreftet at telleren til produktet av tallet og dets gjensidige er 6 og nevneren er 6, og etterlater brøkdel 6/6 som er 1.
Eksempel 2
Den multiplikative inverse på -5 skal ikke forveksles med dets symmetriske (+5) som noen ganger kalles aritmetisk inverse. Den multiplikative inverse vil bli oppnådd som følger:
(-5) ⋅ x = 1
Hvor x er den multiplikative inverse som skal oppnås. En mulig prosedyre består av å fjerne det ukjente x. Som (-5) multipliserer det ukjente X i venstre medlem, så skjer det å dele høyre medlem:
X = 1 / (-5)
Som kjent for + mellom - det er - så er endelig X oppnådd:
X = - ⅕ .
Avslutningsvis - ⅕ er den multiplikative inverse på -5.
Eksempel 3
Få den multiplikative inverse av -20. Anta at den multiplikative inverse er x, da må -2 multiplisert med x være enheten, en betingelse som vi pålegger nedenfor:
-√2 ⋅ x = 1
Begge medlemmene er delt med -√2 for å oppnå:
(-√2 ⋅ x) / (-√2) = 1 / (-√2)
Det første medlemmet er forenklet -"gjenværende:
Det kan tjene deg: Standard estimatfeil: Hvordan det beregnes, eksempler, øvelserX = 1 / (-√2)
Dette uttrykket kan rasjonaliseres, det vil si å eliminere nevnerens rot, multiplisere i telleren med (-√2) og i nevneren for samme mengde slik at resultatet ikke blir endret:
X = (-√2) / [(-√2) (-√2)] =-(√2 / 2)
Avslutningsvis - (√2/2) er den multiplikative inverse (-√2).
Eksempel 4
Anta et hvilket som helst tall X, få din multiplikative inverse og representere det grafisk.
I dette tilfellet er det en funksjon f (x) = x, å oppnå den multiplikative inverse er å finne funksjonen g (x) slik at den er multiplisert med den første av enheten til enheten. G -funksjonen er den gjensidige funksjonen til F og bør ikke forveksles på noen måte med sin inverse funksjon.
Med andre ord, den multiplikative inverse av x er et slikt at følgende er oppfylt:
x ⋅ y = 1
Hvor du skal rydde og ha:
y = 1/x.
Ovennevnte tolkes således gitt en verdi av x, den forrige formelen gir oss sin multiplikative inverse.
Det er mulig å lage sin grafiske representasjon som vist i følgende figur:
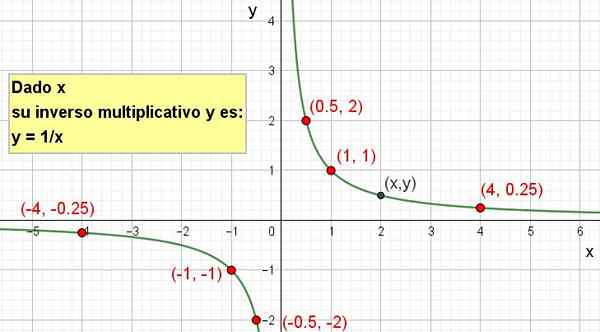 Figur 2. Den multiplikative inverse av x er y = 1/x.
Figur 2. Den multiplikative inverse av x er y = 1/x. Øvelser
Oppgave 1
Gitt x = 2 - √2, få din multiplikative inverse og.
Løsning:
Så det og det er en multiplikativ x x
x ⋅ y = 1
X erstattes av verdien:
(2 - √2) ⋅ y = 1
Så rydder det og:
y = 1 / (2 - √2)
For å rasjonalisere resultatet Multiplies Numerator og nevner med den konjugerte binomialen:
y = (2 + √2) / ((2 + √2) (2 - √2)))
I nevneren gjenkjennes et bemerkelsesverdig produkt som kalles produktet av en sum for en forskjell, som er forskjellen på rutene. På denne måten forsvinner roten i nevneren.
y = (2 + √2) / (2^2 - (√2)^2)
Kan tjene deg: proporsjonÅ løse kreftene:
y = (2 + √2) / (4 - 2)
Forenkle:
y = (2 + √2) / 2
Oppgave 2
Få den multiplikative inverse (1/a + 1/b) der A og B er forskjellige reelle tall.
Løsning:
Vi ringer og den multiplikative inverse av (1/a + 1/b), slik at følgende ligning må oppfylles:
Og ⋅ (1/a + 1/b) = 1
Variabelen er fjernet og:
Y = 1/(1/a + 1/b)
Nevneren er løst:
Y = 1 / ((b + a) / a b)
Som kjent om reglene for algebra, overfører nevneren til nevneren til telleren:
Y = (a b) / (b + a)
Det blir beordret til å endelig skaffe:
(a b)/(a + b) som er den multiplikative inverse av (1/a + 1/b).
Øvelse 3
Få den multiplikative inverse (a - b) / (a^2 - b^2).
Løsning:
Husk at den multiplikative inverse også kalles gjensidig fordi den oppnås bare utveksling av teller og nevner.
Da vil den multiplikative inverse (a - b) / (a^2 - b^2) være:
(A^2 - B^2) / (A - B)
Men dette uttrykket kan forenkles hvis vi i henhold til reglene for algebra, at telleren er en forskjell på firkanter som kan faktorere som et produkt av en sum for en forskjell:
((A + b) (a - b)) (a - b)
Ettersom det er en felles faktor (A - B) i telleren og i nevneren fortsetter vi å forenkle, til slutt oppnå:
(a + b) som er den multiplikative inverse (a - b) / (a^2 - b^2).
Referanser
- Kilder, a. (2016). Grunnleggende matematikk. En introduksjon til beregning. Lulu.com.
- GARO, m. (2014). Matematikk: Kvadratiske ligninger: Hvordan løse en kvadratisk ligning. Marilù Garo.
- Haeussler, e. F., & Paul, r. S. (2003). Matematikk for administrasjon og økonomi. Pearson Education.
- Jiménez, J., Rofríguez, m., & Estrada, r. (2005). Matematikk 1 september. Terskel.
- Dyrebar, c. T. (2005). Matematikkurs 3o. Redaksjonell progreso.
- Rock, n. M. (2006). Algebra jeg er lett! Så lett. Team Rock Press.
- Sullivan, J. (2006). Algebra og trigonometri. Pearson Education.

