Isocuantas og isocostos

Hva er isocuantas og isocostos?

De Isocuantas og isocostos Det er to forskjellige typer kurver som vises som grafiske representasjoner for en gründer for å bestemme den mest effektive produksjonsmetoden for selskapet ditt, det vil si den med den laveste totale kostnaden per produsert enhet.

En isocounta er en kurve der de forskjellige kombinasjonene av to spesifikke produksjonsfaktorer, som en mengde arbeidskraft og maskiner, genererer den samme mengden produsert. Det vil si at det er en kurve som den maksimale produksjonshastigheten er konstant.

De er også kjent som konstante produksjonskurver. Derfor indikerer en isocountakurve de forskjellige kombinasjonene av to produksjonsfaktorer som gir produsenten samme produksjonsnivå per tidsenhet.

Når de kjenner til arten av isokontene, gjennom isokostoslinjene, blir kostnadene for disse faktorene vurdert.

En Isochosto -linje representerer de forskjellige kombinasjonene av to spesifikke produksjonsfaktorer som et selskap kan kjøpe for samme mengde penger, på bekostning siden hver faktor har.

Forskjeller og eksempler

En gründer kunne bruke all sin kapital bare til å kjøpe maskiner eller for å betale lønnen til personalet. Ingen av disse ekstreme situasjonene ville imidlertid tjene. Eller ingen ville betjene maskinene ved ikke å kunne betale lønnen, ellers ville ikke arbeiderne ha de nødvendige maskinene for å gjøre jobben sin.

Derfor må gründeren kombinere på den beste måten det totale arbeidet og maskineriet, under hensyntagen til kostnadene som skal betales for hver av disse faktorene. For å gjøre dette, trekker det en isocostisk linje.

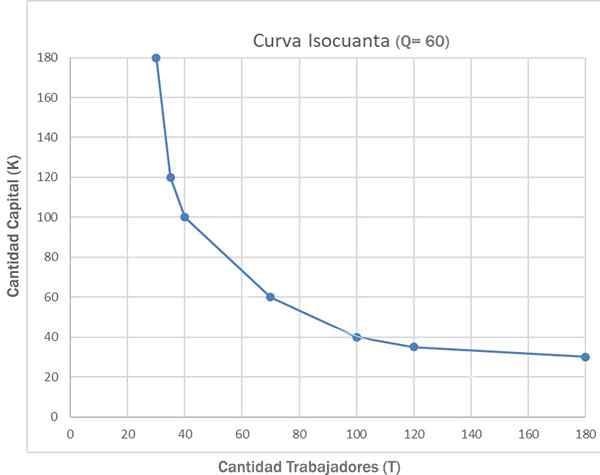
En Isocounta -kurve er en grafisk fremstilling av de forskjellige kombinasjonene av to produksjonsfaktorer, for eksempel arbeid (T) og kapital (K), som genererer samme produksjonsnivå per tidsenhet.

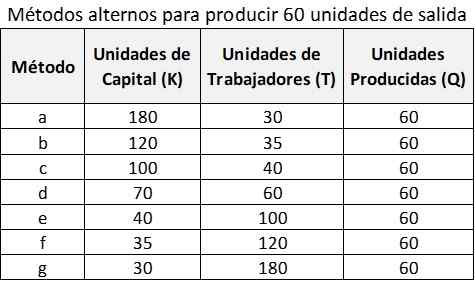
Utgangen produsert av de forskjellige kombinasjonene av T og K kan kalles Q, og være en funksjon av T og K: Q = F (T, K). Følgende tabell viser, med hypotetiske tall, syv mulige kombinasjoner av T og K for å produsere 60 Q -produksjonsenheter:

Isocuanta -kurve

Disse alternativene vises i følgende graf, representert med kurven Q = 60. Derfor kunne selskapet velge kombinasjonen C: (100K og 40T), kombinasjonen G: (30K og 180T) eller noen annen kombinasjon angitt i forrige tabell.

En isocounta viser hva et selskap vil produsere. Presenterer følgende egenskaper:

• Kurven er konveks til opprinnelsen

Dette viser at mengden kapital og arbeidere kan erstatte hverandre. Imidlertid betyr økningen av den ene faktoren reduksjonen av den andre.

• Kurven lener seg ned (den har en negativ skråning)

Dette indikerer at bare samme mengde kan produseres når økningen i enhetene til en produksjonsfaktor blir kompensert med mindre enheter av den andre faktoren. For eksempel kan et selskap få samme produksjonsnivå når kapitalressursen øker, men reduserer arbeidsressursen.

• Kurven skal ikke berøre y- og x -aksen til grafen

Ellers vil den tekniske erstatningsgraden være ugyldig, noe som indikerer at en produksjonsfaktor kan gi ønsket mengde uten noen annen faktor som deltar.

• Du kan ikke krysse kurvene med hverandre

Hvis flere ble trukket i samme graf for å vise at forskjellige mengder ønsket å produsere ikke kunne berøres mellom dem, fordi det skulle indikere at med en kombinasjon av de samme faktorene ville det forekomme den samme mengden i begge deler, noe som er absurd per definisjon.

• Formen på kurven er oval

Som det vil bli sett med isochosto -linjen, er det dette som hjelper til med å bestemme kombinasjonen av lavere kostnader for produksjonsfaktorene som skal brukes.

Isocostlinje

Ikke bare skal du produsere et visst beløp. Gründeren må også ha en viss kapasitet til å kjøpe de nødvendige faktorene for å oppnå det ønskede produksjonsnivået.

Denne kapasiteten vises med sin økonomiske ressurs, det vil si hvor mye penger som er i stand til å bruke kapital og arbeidskostnader, hvis priser blir tatt som konstanter. I dette tilfellet blir kapitalkostnadene bankrenten, og arbeid er arbeiderens lønn.

Dermed må gründeren operere under hensyntagen til en budsjettbegrensning, som er representert av Isocosto -linjen. Derfor, for å finne kombinasjonen av lavere kostnader for faktorene for å produsere de 60 enhetene i eksemplet, må den bygge en slik isokose.

Dermed er isokostoen en grafisk representasjon som viser de forskjellige kombinasjonene som kan skaffes fra produksjonsfaktorene som har en viss mengde penger. Derfor representerer hvert punkt i isochosto -linjen den samme mengden.

• Hvordan gjøres det

For å avgrense denne linjen med isokosto, må markedsprisene for disse to faktorene ha blitt undersøkt. Anta for eksempel at prisen på kapital er $ 40 per enhet og prisen på arbeidskraft er $ 20 per enhet.

Således, hvis enhetskostnaden for arbeidsenheten (t) er w = $ 20 og enhetskostnadene for kapitalenheten (k) er r = $ 40, så er den totale kostnaden C = WT + RK.

Derfor, hvis et totalt beløp er tilgjengelig C = $ 3.600, kan du kjøpe 90r+0W, 0R+180W eller andre kombinasjoner, for eksempel 50R+80W. Alle disse og andre kombinasjoner vises i følgende graf, ved hjelp av Isochosto Line C = $ 3.600.

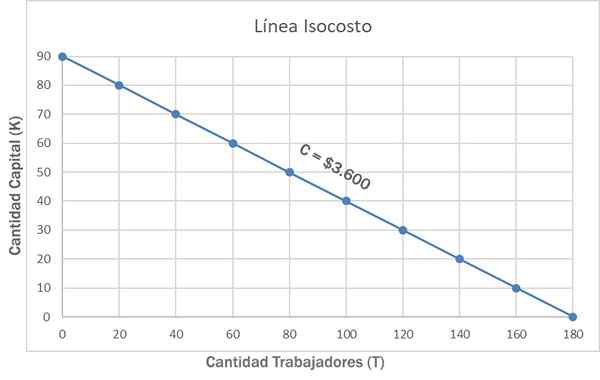
Ettersom prisen på hver faktor ikke varierer, er isokostoen en rett linje. På den annen side er skråningen negativ fordi den representerer forholdet mellom kostnadene for arbeidskraft og kapital: W / R. Det er kjent som faktorers substitusjonshastighet, som arbeidsfaktoren kan erstattes av kapitalfaktoren.

Minimering av kostnadene

Selskapet må forsøke å minimere kostnadene for å produsere et visst produksjonsnivå. For å finne kombinasjonen av lavere kostnader for faktorene for et fast produksjonsnivå, kombineres grafikken til isocountakurven med den for isochosto -linjen.

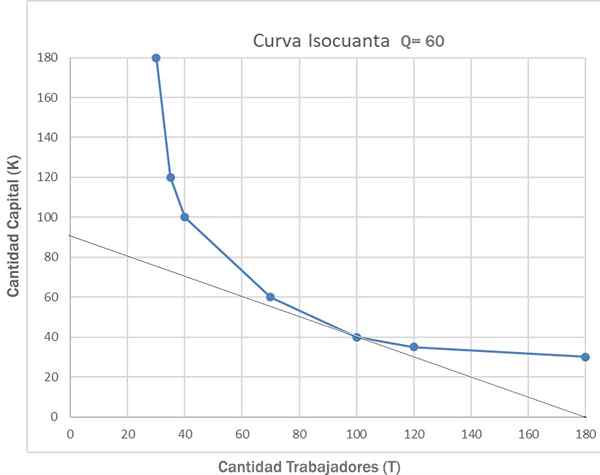
Selskapet vil prøve å finne kombinasjonen av rimeligere faktorer i hele isokounten. Det vil være den laveste kostnadsposisjonen der Isocount.

Dermed oppnås produksjonsoptimalisering når prisene på faktorene og beløpet som skal produseres er lik. For dette eksemplet vil minimumskostnadspunktet være "E" -kombinasjonen av tabellen: k = 40 og t = 100.

Referanser

1. Smriti Chand (2021). Laws of Return: The Isoquant-Isocost Approach | Økonomi. Artikkelbiblioteket ditt. Hentet fra: yourarticlelibrary.com.
2. Netescuela (2021). Isocuantas og isocostos. Hentet fra: Netescuela.org.
3. Will Kenton (2020). Isquant kurve. Inventopedia. Hentet fra: Investopedia.com.
4. Nipun s. (2021). Isoquant og isocost linjer (med diagram). Økonomisk diskusjon. Tatt fra: EconomicsDiscusion.nett.
5. Wikieducator (2021). Isoquant og isocost itexon. Hentet fra: wikieducator.org.