Ampère formel og ligningsrett, demonstrasjon, øvelser

De Ampère Law sier at sirkulasjonen av den magnetiske induksjonsvektoren B Det er proporsjonalt med intensiteten og strømmen som flyter av det samme.

I sin tur sirkulasjonen av B Det er summen av alle produktene mellom tangentialkomponenten B_║ og lengden på et lite segment Δℓ av en lukket kurve C, Rundt en krets. I matematiske termer er det skrevet slik:

∑ b_║ .Δℓ ∝ Yo

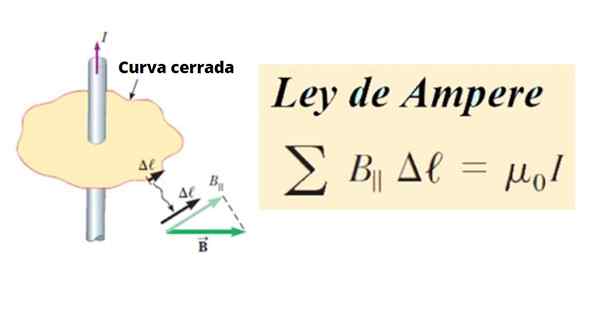
Figur 1. Definisjon av ampere -loven. Kilde: Serway, R. College Physics.

Som en vilkårlig linje eller kurve kan den deles inn i små segmenter Δℓ, Og disse kan igjen være uendelige, så kalles de Dℓ.

I dette tilfellet blir summen en integrert linje av skalarproduktet mellom vektorene B og ds. Dette produktet inneholder den tangensielle komponenten i B, som er B cosθ, hvor θ er vinkelen mellom vektorene:

Den lille sirkelen som krysser den integrerte betyr at integrasjon utføres på en lukket bane C, som i dette tilfellet involverer strømmen som strømmer gjennom førerens tverrsnitt.

Proporsjonalitetskonstanten som er nødvendig for å etablere likhet er μ_enten, Vakuumpermeabilitet. På denne måten gjenstår Ampères lov:

Ampères lov forteller oss at linjen integrerte ∫_C B ∙ Ds Det er verdt nøyaktig μ_entenJeg, men det tilbyr oss ikke detaljene om hvordan magnetfeltet er orientert B Angående kurve C på hvert punkt, eller om hvordan du beregner integralen. Det forteller oss bare at resultatet av det samme alltid er μ_entenYo.

[TOC]

Demonstrasjon av Ampères lov

Ampères lov blir bekreftet eksperimentelt å sjekke magnetfeltet produsert av en veldig lang rettlinjet dirigent. Før du tar opp problemet, må to tilfeller av spesiell interesse i den forrige ligningen fremheves:

Det kan tjene deg: lysende kropper: egenskaper og hvordan de genererer sitt eget lys

-Den første er når B og ds De er parallelle, noe som betyr det B er tangensiell for C. Da er vinkelen mellom begge vektorene 0º og skalarproduktet er ganske enkelt produktet av størrelsen B.ds.

-Det andre oppstår hvis B og ds De er vinkelrett, i hvilket tilfelle skalarproduktet er 0, siden vinkelen mellom vektorene er 90º, hvis kosinus er 0.

En annen viktig detalj er valget av kurve C som feltsirkulasjonen blir evaluert. Ampères lov spesifiserer ikke hva den kan være, men den må pakke den nåværende distribusjonen. Det står heller ikke hvordan du skal reise kurven, og det er to muligheter for dette.

Løsningen er å tilordne skilt i henhold til høyre tommelregel. De fire fingrene er buede i den retningen du vil integrere, vanligvis vil dette være det samme i feltet B sirkulerer. Hvis strømmen peker i retning av høyre tommel, tildeles et skilt og hvis ikke, tegn -.

Dette gjelder når det er en distribusjon med flere strømmer, noen kan være positive og andre negative. Den algebraiske summen av dem er det vi skal plassere i loven til Ampère, som vanligvis er utnevnt til som Utrengt strøm (For kurven C).

Magnetfelt av rettlinjet og uendelig ledning

Figur 2 viser en ledning som transporterer en strøm og ut av flyet. Høyre tommelregler sikrer det B Det sirkulerer i motsatt retning, og beskriver omkretser som Red Arrows viser.

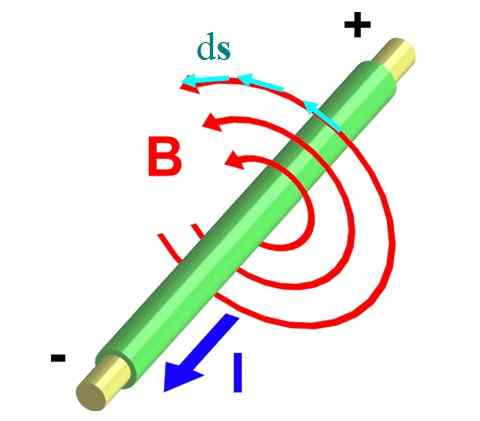Figur 2.- Magnetfelt av en uendelig ledning. Kilde: Wikimedia Commons.

La oss ta en av dem, hvis radius er r. Vi deler det inn i små differensialsegmenter Ds, representert ved hjelp av blå vektorer. Begge vektorene, B og ds, De er parallelle på hvert punkt i omkretsen, og på denne måten den integrerte ∫_C B ∙ Ds Det forvandler seg inn:

Kan tjene deg: Diktstrøm

∫_C Bds

Dette er fordi, som vi sa før, skalarproduktet B ∙ Ds  Det er produktet av størrelsene på vektorene ved 0º cosinus. Resultatet av integralen er kjent takket være Ampères lov, derfor skriver vi:

∫_C BDS = μ_entenYo

Siden størrelsen på feltet er konstant over hele banen, etterlater det integralen:

B ∫_C Ds = μ_entenYo

Integralet ∫_C DS representerer summen av alle uendelige segmenter som utgjør radioomkrets r, Tilsvarer dens lengde, produktet av sin radius med 2π:

B.2πr = μ_entenYo

Og derfra finner vi at størrelsen på B er:

B = μ_entenI / 2πr

Det er nødvendig å understreke at selv om den valgte banen (eller Amperian Circuit) Ikke sirkulært, resultatet av integralen fortsetter å være μ_entenJeg, men ∫_C B ∙ Ds Det ville ikke lenger være B.2πr.

Det er grunnen til at nytten av Ampères lov for å bestemme magnetfeltet ligger i valg av distribusjoner med høy symmetri, slik at integralen er lett å evaluere. Sirkulære og rettlinjede baner oppfyller dette kravet.

Løste øvelser

- Oppgave 1

Tenk på kurver A, B, C og D vist i figur 3. De pakker tre strømmer, to som forlater flyet, symbolisert med ett punkt ( . ), hvis intensitet er 1 a og 5 a, og en strøm som kommer inn i flyet, som er betegnet med et kors og hvis størrelse er 2 a.

Finn strømmen som er omsluttet av hver kurve.

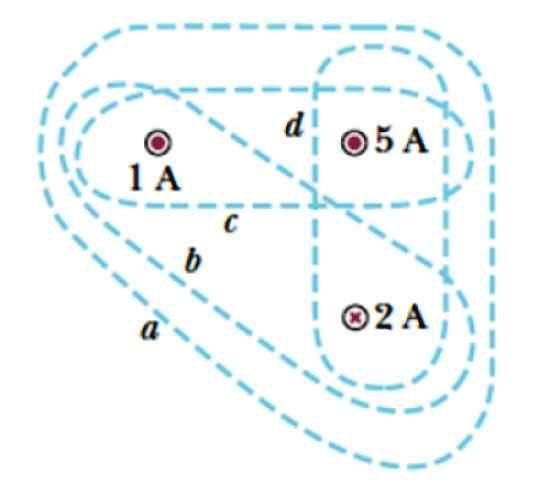Figur 3. Flere kurver for å anvende Ampères lov. Kilde: Serway, R. College Physics.

Løsning

Strømmene som forlater papiret blir tildelt et skilt +. I følge dette:

Det kan tjene deg: Overfladiske bølger: Karakteristikker, typer og eksempler

Kurve a

Omslutter de tre strømningene, derfor er den lukkede strømmen + 1 a + 5 a - 2 a = 4 a.

Kurve b

Bare strømningene til 1 a y - 2 a er inne i denne kurven, derfor er den lukkede strømmen fra - 2 a.

Kurve c

Inneholder utgående strømninger 1 og 5 A, derfor er den lukkede strømmen 6 a.

Kurve d

Strømmene inni er +5 a og - 2 a, og vedlegger deretter en nettstrøm på 3 til.

- Oppgave 2

Beregn størrelsen på magnetfeltet produsert av en veldig lang rettlinjetråd.

Løsning

I henhold til Ampères lov er ledningsfeltet gitt av:

B = μ_entenI / 2πr = (4π x 10^-7 x 1/2π x 1) t = 2 x 10^-7 T.

Referanser

1. Figueroa, d. (2005). Serier: Fysikk for vitenskap og ingeniørfag. Volum 6. Elektromagnetisme. Redigert av Douglas Figueroa (USB).
2. Knight, r.  2017. Fysikk for forskere og ingeniørfag: En strategitilnærming.  Pearson.
3. Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Ed. Volum 2.
4. Serway, r. 2009. College Physics. Cengage Learning.
5. Tipler, s. (2006) Fysikk for vitenskap og teknologi. 5. utg. Volum 2. Redaksjon tilbake.