Coulomb lov forklaring, formel og enheter, øvelser, eksperimenter

De Coulomb Law Det er den fysiske loven som styrer samspillet mellom elektrisk belastede objekter. Det ble uttalt av den franske forskeren Charles Augustin de Coulomb (1736-1806), takket være resultatene fra eksperimentene hans gjennom torsjonsbalanse.

I 1785 opplevde Coulomb utallige tider med små elektrisk ladede sfærer, for eksempel å bringe eller bort to kuler, som varierer størrelsen på belastningen og også skiltet. Alltid se og registrere hvert svar nøye.

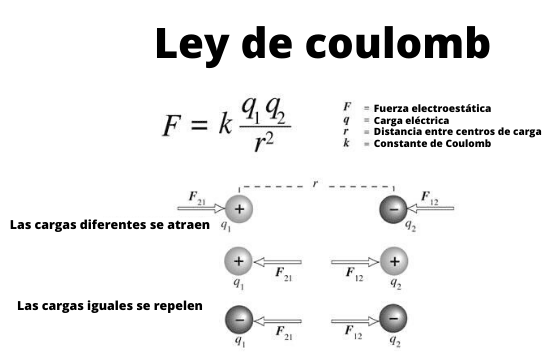
Figur 1. Ordning som viser samspillet mellom spesifikke elektriske kostnader gjennom Coulombs lov.

Disse små områdene kan betraktes som spesifikke belastninger, det vil si objekter hvis dimensjoner er ubetydelige. Og de oppfyller, som kjent siden de gamle grekernes tid, at belastningene på det samme tegnet er frastøtt og de med forskjellige tegn blir tiltrukket.

Figur 2. Militæringeniør Charles Coulomb (1736-1806) regnes som den viktigste fysikeren i Frankrike. Kilde: Wikipedia Commons.

Med dette i bakhodet fant Charles Coulomb følgende:

-Tiltrekningskraften eller frastøtningen mellom to spesifikke ladninger er direkte proporsjonal med produktets størrelse på belastningen.

-Denne styrken er alltid rettet langs linjen som blir med i lastene.

-Endelig er styrken på kraften omvendt proporsjonal med kvadratet på avstanden som skiller belastningen.

[TOC]

Formel og enheter i Coulomb -loven

Takket være disse observasjonene konkluderte Coulomb med at styrken på styrken F Mellom to spesifikke ladninger q₁ og q₂, separert en avstand r, Det er matematisk gitt som:

Ettersom kraft er en vektorstørrelse, for å uttrykke den, er en enhetsvektor fullstendig definert r I retning av linjen som fester lastene (en enhetsvektor har størrelsesorden lik 1).

I tillegg kalles den nødvendige proporsjonalitetskonstanten som transformerer det forrige uttrykket til en likhet k_og eller ganske enkelt k: elektrostatisk konstant enten Coulomb konstant.

Til slutt etableres Coulomb -loven for punktlige belastninger, gitt av:

Styrken, som alltid i det internasjonale systemet med enheter, kommer i Newton (N). Når det gjelder anklagene, kalles enheten Coulomb (C) til ære for Charles Coulomb, og til slutt kommer avstanden R i meter (m).

Attendig observasjon av den forrige ligningen, er det klart at den elektrostatiske konstanten må ha enheter av n.m² / C², Å skaffe Newtons som et resultat. Verdien av konstanten ble bestemt eksperimentelt som:

Kan tjene deg: gratis vektorer: egenskaper, eksempler, øvelser

k_og = 8.89 x 10 ⁹ N.m² / C² ≈ 9 x 10 ⁹ N.m² / C²

Figur 1 illustrerer samspillet mellom to elektriske ladninger: Når de er det samme tegnet, blir de frastøtt, ellers tiltrekker de seg.

Legg merke til at Coulombs lov passer Newtons tredje lov eller lov om handling og reaksjon, derfor størrelsene på F₁ og F₂ De er de samme, adressen er den samme, men sansene er motsatte.

Hvordan anvende Coulombs lov

For å løse interaksjoner mellom elektriske kostnader, må følgende tas i betraktning:

- Ligningen brukes utelukkende i tilfelle av spesifikke belastninger, det vil si elektrisk belastede objekter, men av veldig små dimensjoner. Hvis belastede objekter har målbare dimensjoner, er det nødvendig å dele dem i veldig små belastninger og deretter legge til bidragene til hver av disse belastningene, for hvilken omfattende beregning er nødvendig.

- Elektrisk kraft er en vektorstørrelse. Hvis det er mer enn to ladninger som samhandler, er nettokraften på belastningen Q_Yo Det er gitt av superposisjonsprinsippet:

F_Nett = F_i1 + F_I2 + F_i3 + F_i4 +... = ∑ F_ij

Hvor abonnementet J Vale 1, 2, 3, 4 ... og representerer hver av de gjenværende belastningene.

- Det må alltid være i samsvar med enhetene. Det hyppigste er å jobbe med den elektrostatiske konstanten i enheter hvis du må sørge for at lastene er i Coulomb og avstandene i meter.

- Endelig blir ligningen brukt når belastningene er i statisk balanse.

Løste øvelser

- Oppgave 1

I den følgende figuren er det to spesifikke belastninger +Q og +2Q. En tredje punktlig belastning -Q er plassert på P. Det blir bedt om å finne den elektriske kraften på denne belastningen på grunn av tilstedeværelsen av de andre.

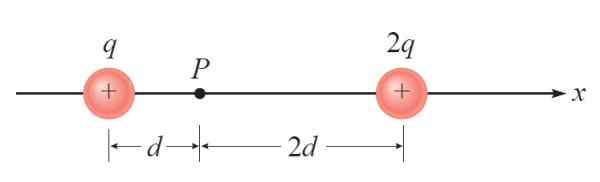Figur 3. Diagram for året løst 1. Kilde: Giambattista, a. Fysikk.

Løsning

Den første tingen er å etablere et passende referansesystem, som i dette tilfellet er den horisontale aksen eller x -aksen. Opprinnelsen til dette systemet kan være hvor som helst, men med komfort vil det bli plassert i P, som vist i figur 4A:

Kan tjene deg: Bethelgeuse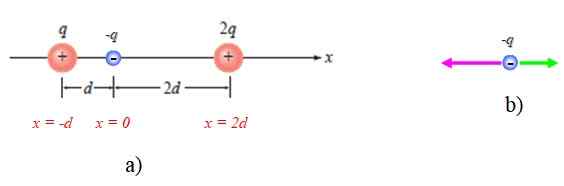Figur 4. Ordningen for året løst 1. Kilde: Giambattista, a. Fysikk.

Et skjema for kreftene på -Q vises også, under hensyntagen til at det tiltrekkes av de to andre (figur 4B).

La oss ringe F₁ Til kraften som utøver belastningen som på belastningen -Q, er de rettet langs X -aksen og peker i negativ forstand:

Enhetsvektoren i retning av x -aksen er x Med en circumflex -aksent i ligningen. Dette er en vanlig notasjon for en enhetsvektor. Det mindre tegnet vises fordi styrken F₁ peker i den negative forstand av aksen.

Analog beregnes F₂:

Merk at størrelsen på F₂ Det er halvparten av F₁, Selv om belastningen er dobbelt. For å finne nettokraften, blir de endelig lagt til vektorly F₁ og F₂:

F_Nett = (-k + k/2).(Q² /d²) (x) N = - (k/2).(Q² /d²) (x) N

- Oppgave 2

To polystyrenfærer med lik masse m = 9.0 x 10^-8 kg har den samme positive belastningen Q og er suspendert av en silketråd i lengde L = 0,98 m. Kulene er atskilt en avstand på d = 2 cm. Beregne verdien av.

Løsning

Situasjonen for uttalelsen er beskrevet i figur 5a.

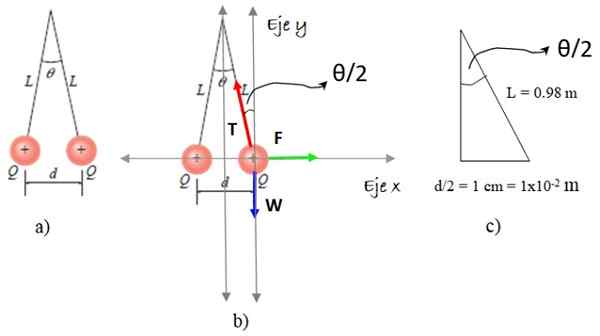Figur 5. Ordninger for oppløsning av trening 2. Kilde: Giambattista, a. Fysikk /f. Zapata.

Vi valgte en av sfærittene, og på den tegner vi det isolerte kroppsskjemaet, som inkluderer tre krefter: vekt W, Tauspenning T og elektrostatisk frastøtning F, Som vises i figur 5b. Og nå trinnene:

Trinn 1

Verdien av θ/2 beregnes med trekanten i figur 5c:

θ/2 = Arcsen (1 x 10^-2/0.98) = 0.585º

Steg 2

Da må du bruke Newtons andre lov og match 0, siden kostnadene er i statisk balanse. Det er viktig å fremheve den spenningen T Den er tilbøyelig og har to komponenter:

∑f_x = -T.sin θ + f = 0

∑f_og = T.cos θ - w = 0

Trinn 3

Vi fjerner størrelsen på spenningen til den siste ligningen:

Det kan tjene deg: Dynamikk: Historie, hvilke studier, lover og teorier

T = w/ cos θ = mg/ cos θ

Trinn 4

Denne verdien erstattes i den første ligningen for å finne størrelsen på f:

F = t sin θ = mg (sin θ / cos θ) = mg. Tg θ

Trinn 5

Som f = k q² /d², Det rydder Q:

Ved å erstatte de numeriske verdiene gitt av uttalelsen, oppnås det:

Q = 2 × 10^-elleve C.

Eksperimenter

Å sjekke Coulombs lov er enkel ved hjelp av en torsjonsbalanse som ligner på den som ble brukt på laboratoriet hans.

Det er to små sfærer av Saúco, hvorav den ene, den i midten av balansen, er suspendert fra en tråd. Eksperimentet består i å berøre Saúco -sfærene lastet ned med en annen metallfære lastet med belastning Q.

Figur 6. Coulombs torsjonsbalanse.

Umiddelbart distribueres belastningen likt mellom de to Saúco -sfærene, men da, som er masse av det samme tegnet, frastøter de seg. En kraft som forårsaker trådens torsjon fra tråden og straks beveger seg bort fra den faste sfæren virker på den suspenderte sfæren.

Så ser vi at det varierer noen ganger til balansen når. Deretter er torsjonen av stangen eller tråden som holder den balansert av den elektrostatiske frastøtningskraften.

Hvis sfærene opprinnelig var på 0, vil nå den mobile sfæren ha snudd en vinkel θ. Rundt balansen er det et kandidatbånd i grader for å måle denne vinkelen. Når du tidligere bestemmer torsjonskonstanten, blir frastøtningskraften og verdien av belastningen anskaffet av Saúco -sfærene lett beregnet.

Referanser

1. Figueroa, d. 2005. Serier: Fysikk for vitenskap og ingeniørfag. Volum 5. Elektrostatikk. Redigert av Douglas Figueroa (USB).
2. Giambattista, a. 2010. Fysikk. Andre utgave. McGraw Hill.
3. Giancoli, d.  2006. Fysikk: Prinsipper med applikasjoner. 6. Ed Prentice Hall.
4. Resnick, r. 1999. Fysisk. Vol. 2. 3. utg. på spansk. Continental Editorial Company s.TIL. Av c.V.
5. Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14. Ed. Volum 2.