Darcy lov

Vi forklarer hva som er Darcy's lov, dens ligninger, anvendelser, begrensninger og foreslår en øvelse som skal løses

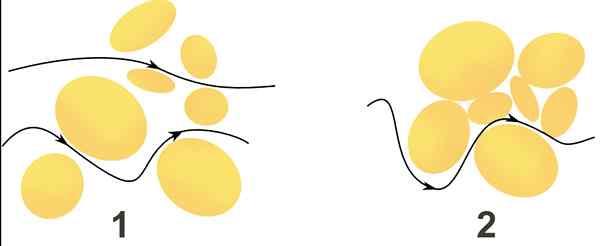
Vannstrøm gjennom to porøse medier er indikert gjennom svarte piler. I medium 1 beveger strømmen seg raskere enn i Middle 2, siden hastigheten avhenger av størrelsen på mellomtallene og enkel kommunikasjon mellom dem. Kilde: Wikimedia Commons.

Hva er Darcy's lov?

De Darcy lov Det er et matematisk forhold som gjelder strømmen av væsker i permeable eller porøse medier, for eksempel vannet som drenerer i sanden.

Når væsken går videre gjennom det porøse, varer det hydrostatiske trykket. På denne måten vises konseptet med hydraulisk gradient, en fysisk mengde som vil bli betegnet med bokstaven I.

På den annen side er det porøse mediet preget av en mengde som kalles Hydraulisk konduktivitet K. There is clearly a relationship between the porosity, determined by K, the hydraulic gradient I and the flow per unit of cross section Q Q.

Forholdet mellom dem ble oppdaget av den franske hydrauliske ingeniøren Henry Darcy (1803-1858), som hadde ansvaret for vannforsyningen til hjembyen: Dijon.

Darcy's lov ble presentert i 1856, i et grundig arbeid der de fysiske beløpene som er involvert i loven er detaljert, eksperimentene som ble utført og veldig spesielt et apparat som ble kalt Permemeter.

Darcy Law Equations

Darcys lov viser forholdet mellom flere fysiske mengder som beskriver strømmen gjennom et porøst medium. Det indikerer at vannstrømmen Q som beveger seg gjennom et visst porøst middel er direkte proporsjonalt med tverrsnittet gjennomboret til og den hydrauliske gradienten Yo:

Q ∝ a ∙ i

Kan tjene deg: ensartet rettlinjet bevegelse: egenskaper, formler, øvelser

Proporsjonalitetskonstanten er permeabiliteten K i det porøse miljøet, også kalt Hydraulisk konduktivitet. På denne måten blir Darcy's lov presentert som:

Q = k ∙ a ∙ i

Differensiell form for Darcy's lov

Darcys ligning kan uttrykkes som et forskjellig forhold mellom strømningshastigheten på hvert punkt og den lokale hydrauliske gradienten:

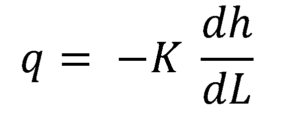
Siden den hydrauliske gradienten er en negativ mengde når den beregnes i strømningsretningen, er det da nødvendig å multiplisere med det negative av hydraulisk konduktivitet for å oppnå den gjennomsnittlige strømningshastigheten q, i hvert tverrsnitt.

Da blir størrelsene som er til stede i Darcys lov analysert mer detaljert.

Flyt, hydraulisk gradient og permeabilitet

1.- Flyt q

Strømmen er definert som vannvolumet som sirkulerer gjennom et visst tverrsnitt til strømningsretningen, per tidsenhet:

Q = ΔV / Δt

I det internasjonale systemet med SI -enheter måles strømmen i kubikkmeter per sekund, men den kommer ofte til uttrykk i liter per minutt eller liter per sekund.

Flyt per enhet av Q -området er ofte nødvendig, som er forholdet mellom Q -strømmen og tverrsnittet:

q = q / a

I SI uttrykkes Q i M/s, og det er grunnen til at Q representerer væskens gjennomsnittlige hastighet i tverrsnittet av røret.

Det er viktig å merke seg at selv om strømmen Q er den samme i alle seksjoner av røret, er strømmen per enhet q eller ganske enkelt strømningshastigheten høyere i de smaleste og mindre seksjonene i de bredere.

2.- Hydraulisk gradient i

Når en væske sirkulerer langs et porøst medium, reduseres hydrostatisk trykk i samme retning av strømmen.

Kan tjene deg: tonn: transformasjoner, ekvivalenser og øvelser løst

Det er kjent at det hydrostatiske trykket, på et bestemt punkt i røret, er proporsjonalt med høyden H som markerer et åpent rørtrykksmåler på det stedet. Proporsjonalitetskonstanten er et produkt av væsketetthet på grunn av tyngdekraftakselerasjon.

På denne måten er den hydrauliske gradienten I definert som forholdet mellom høydeforskjellen ΔH for søylene til to manometre og ΔL, sistnevnte er avstanden som skiller manometrene (se figuren nedenfor):

I = ΔH / ΔL

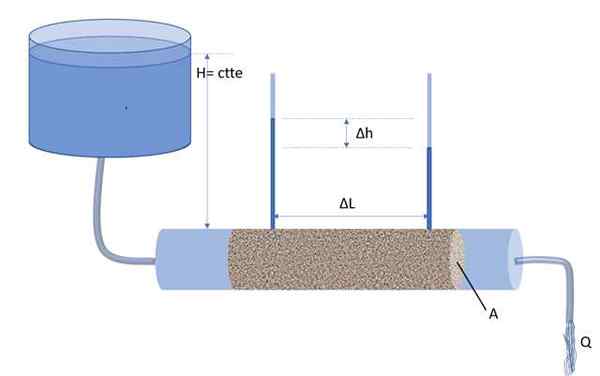Permemeter, et apparat oppfunnet av Henry Darcy for å kvantifisere vannstrømmen gjennom et porøst medium. Kilde: f. Zapata.

Dette er den gjennomsnittlige hydrauliske gradienten i delen av lang ΔL, en dimensjonsløs mengde og også negativ.

Hvis du vil finne den hydrauliske gradienten på hvert punkt i røret, blir grensen tatt for å ha en tendens til null, noe som resulterer i derivatet av den hydrauliske gradientfunksjonen med hensyn til posisjon L, langs strømmen:

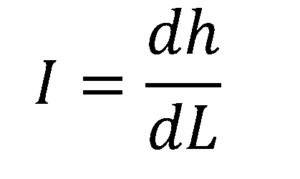
3.- Permeabilitet k

Permeabiliteten til et porøst middel eller hydraulisk konduktivitet er forholdet mellom strømmen Q og produktet av tverrsnittet TIL For den hydrauliske gradienten Yo:

K = q / a ∙ i

Hydraulisk konduktivitet har hastighetsenheter, meter over seg selv.

En enhet for k er blitt definert, kalt Darcy, Til ære for Henry Darcy og definert som følger:

EN Darcy Det er permeabiliteten til en flytende milliliter, med en viskositet av en centipoise, som beveger seg langs en centimeter i et differensialtrykk av en atmosfære, gjennom et tverrsnitt av en kvadratcentimeter.

Darcy Law Applications

Den viktigste anvendelsen av Darcy's lov er å forutsi vannstrømmen langs en akvifer, før du borer brønner.

Kan tjene deg: dimensjonal analyse

Darcy's lov brukes også regelmessig i landbruks- og hydrologisk ingeniørfag. Det kan også brukes i oljeindustrien for å beskrive strømmen av gass og olje i porøse medier. Imidlertid kan k i så fall variere, avhengig av strømmen av gass eller olje, og kanskje ikke bare avhenger og utelukkende avhenger av det permeable underlaget.

Begrensninger

Darcy's lov antar at den hydrauliske konduktiviteten k er en mengde av mediet, noe som er sant i mange tilfeller. Noen ganger avhenger imidlertid k av væskens dynamiske viskositet, som igjen kan avhenge av strømningshastigheten og temperaturgradientene.

Darcys antagelse er plausibelt når man vurderer underjordisk vann, der viskositeten er praktisk talt konstant, siden verdien nesten ikke påvirkes med tanke på de få temperaturforskjellene i akviferen.

I tilfeller av oljestrøm gjennom porøse midler, kan ikke Darcy -ligningen brukes som presentert her, men visse modifikasjoner er innarbeidet som går utover formålet med denne artikkelen.

Trening løst

Bestem den hydrauliske konduktiviteten til en strandsand, ved å bruke et laboratorium permemeter.

Anta at permemeterrøret har en diameter på 20 cm og at avstanden mellom de to manometrene er 50 cm. Det er også kjent at vann strømmer med en hastighet på 300 kubikk desimeter per minutt og nivåforskjellen mellom de to manometrene er 25 cm.

Løsning

Flyten som er 300 kubikk desimeter per minutt, men som uttrykker i enheter av det internasjonale systemet, ville det være slik:

Q = 300 x 10^-3 m³ / 60 s = 5 x 10^-3 m³ / s

Tverrsnitt A er beregnet av:

A = π ∙ r² = π ∙ (10 cm)² = π ∙ (0,1 m)² = 0,314 m²

Hydraulisk gradient I er en kvotient mellom den manometriske høydeforskjellen og separasjonen av manometrene:

I = 25 cm / 50 cm = 0,5

I henhold til definisjonen av hydraulisk konduktivitet K gitt ovenfor:

K = q / a ∙ i = (5 x 10^-3 m³ / s) / (0,314 m² ∙ 0,5) = 3,185 x 10^-2 m/s ≈ 2 m/min.