Hess forklaringslov, søknader, eksempler

De Hess lov Det er en annen manifestasjon av energibesparelsesloven som gjør det mulig å bestemme, gjennom enkle algebraiske summer, entalpien til en kjemisk reaksjon. Forstått ved entalpi som varmen som frigjøres eller absorberes, ved konstant trykk, som er assosiert med enhver kjemisk reaksjon eller kjemisk fenomen.

Enthalpies, ΔH, bestemmes eksperimentelt ved bruk av kalorimetri. Imidlertid er det reaksjoner som er vanskelige å studere med denne teknikken. Når dette skjer, brukes andre reaksjoner som deres spesifikke entalpier har, og som har interessene eller forbindelsene som interesserer.

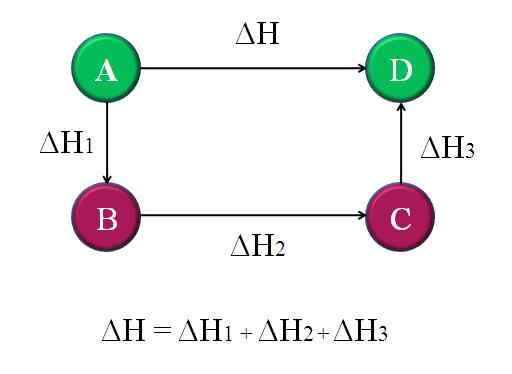
Enkelt og generelt diagram der Hess -loven for fire kjemiske reaksjoner blir brukt. Kilde: Gabriel Bolívar.

På denne måten kan den "ukjente" ΔH av reaksjonen beregnes. For eksempel hjelper toppdiagrammet til å forstå denne ideen. Det er fire reaksjoner: A-D, A-B, B-C og C-D. A-D-reaksjonen er den som har den største ΔH, fordi de forekommer, så å si, de mest beryktede kjemiske endringene.

De andre reaksjonene, mens, har mindre ΔH, siden de består av alternative trinn eller alternative reaksjoner for å nå de samme produktene d. Derfor summen av Δh₁, ΔH₂ og ΔH₃, Det vil være lik Δh. Å vite dette, ΔH, eller noen annen entalpi, kan beregnes ved å bruke enkle rydding. Dette er Hess's lov.

Hess's lov er veldig nyttig når du beregner reaksjonsentalpier, samt treningsentalpier for forskjellige forbindelser eller ustabile mellommenn.

[TOC]

Forklaring av Hess's lov

Beregning av entalpien av en reaksjon

Årsaken til at det er oppfylt det:

ΔH = ΔH₁ + ΔH₂ + ΔH₃

Det er fordi entalpi, eller endring av entalpi, er en tilstandsfunksjon. Dette betyr at verdiene deres ikke blir endret etter antall trinn, trinn eller mellomreaksjoner. For eksempel vil ΔH forbli den samme selv når det er en ΔH₁₀ som bør vurderes i den algebraiske summen.

Entalpier kan visualiseres som toppen av noen fjell. Uansett hvordan trinnene mot dem er rettet, vil høyden som skiller dem fra MAR -nivået aldri variere. Og nettopp er det høydene som blir lagt til eller trukket fra for å bestemme den ukjente høyden på et omkringliggende fjell.

Tilbake til forrige diagram: A er det et fjell, av et annet fjell, og så videre. Høydeforskjellen mellom A- og D -topper, er den største. Legger til høydene mellom A-B, B-C og C-D, vil det gi lik A-D-høyden. Dette er hva som gjøres med entalpiene til deres respektive kjemiske reaksjoner.

Kan tjene deg: fosfatgruppe

Entalpi av en reaksjon fra entalpier av formasjoner

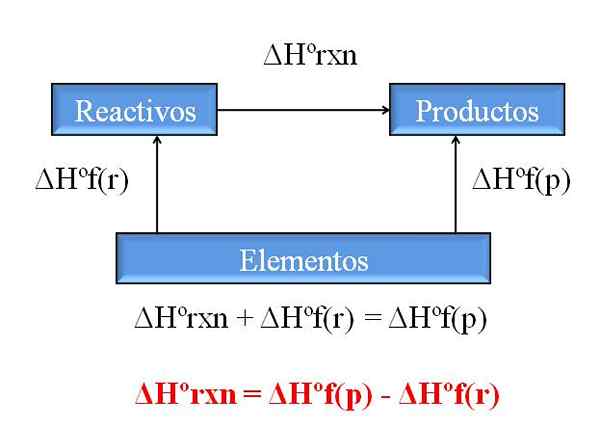Generelt diagram for å beregne entalpien til en reaksjon fra entalpies av formasjoner. Kilde: Gabriel Bolívar.

En av de mest verdifulle konsekvensene av Hess lov er at den tillater bestemmelse av entalpiene til enhver kjemisk reaksjon, og tar treningsentalpiene til alle forbindelser (reagenser og produkter) involvert involvert.

Det overlegne bildet illustrerer dette poenget. Forstått ved entalpi av tilhørende varmetannelse når en forbindelse dannes fra elementene. Denne entalpien ville bli den maksimale mulige forskjellen mellom reagenser og produkter, uten behov for å konsultere andre kjemiske reaksjoner; I det minste utenfor separat trening av forbindelser.

Hvordan leser du diagrammet denne gangen? Et triks er alltid å legge til entalpiene når det går i retning av pilen, og trekke dem fra dem når pilen er på motsatt rute. Således tilfører ΔHºrxn, standard reaksjonsentalpi, til ΔHºF (reagenser), standard entalpi av reagensdannelse, og de blir trukket fra ΔHºF (produkter), standard entalpi av produktdannelse av produkter.

Reaksjoner summerer

Diagrammene kan bli veldig kompliserte å tolke, spesielt når det er mange reaksjoner som må vurderes. Derfor brukes summen av reaksjonene. Denne metoden letter beregningen av entalpier i stor grad, og fremskynder forståelsen av Hess lov.

Anta for eksempel at du vil bestemme ΔHºRXN for følgende reaksjon:

A + B + C → ABC

Og vi har også to andre reaksjoner:

A + B → AB (ΔHº₁)

AB + C → ABC (ΔHº₂)

Det er interessant at A + B + C er på venstre side (reagenser) og at ABC er på høyre side (produkter). Deretter fortsetter vi ganske enkelt å legge til de to siste reaksjonene:

A + B → AB

AB + C → ABC

A + ab + c → abc + ab

Som AB er fra begge sider elimineres det. Og slik har vi:

A + B + C → ABC

ΔHºrxn = ΔHº₁ + ΔHº₂

Ved å legge til reaksjonene, blir bruken av et hvilket som helst diagram utelatt.

Anvendelser av Hess's lov

Hess's lov tillater, uten behov for eksperimenter, entalpier for forskjellige kjemiske reaksjoner eller fenomener. Noen av dem er oppført:

- Treningsentalpier for ustabile forbindelser eller mellommenn, som vi vanligvis har i organisk kjemi.

-Entalpier av faseoverganger, i studiet av krystallinske faste stoffer.

Kan tjene deg: kjemisk forbindelse

-Entalpier av allotropiske overganger, for eksempel den mellom grafitt og diamant.

På samme måte brukes Hess's lov for å bestemme retikulær energi til et fast stoff, og de elektroniske tilknytningene til noen atomer.

Eksempler: Løste øvelser

- Eksempel 1

Beregn Δhrxn for følgende reaksjon:

2HCl (g) + f₂(g) → 2HF (L) + CL₂(g)

Hvis du har følgende reaksjoner og deres respektive entalpier:

4HCl (g) + eller₂(g) → 2H₂Eller (l) + 2cl₂(g) (ΔH = -202.4 kJ/mol)

1/2H₂(g) + 1/2f₂(g) → HF (L) (ΔH = -600.0 kJ/mol)

H₂(g) + 1/2o₂(g) → h₂Eller (l) (Δh = -285.8 kJ/mol)

Ligninger bestilling

For å starte, må vi legge til reaksjonene på en slik måte at HCl og F₂ er på venstre side, og HF og CL₂, På høyre side. Men viktigere er det å merke at så mye h₂ som h₂Eller er ikke i interesse -ligningen. Derfor må vi avbryte dem i summen, og lage de støkiometriske koeffisientene sammenfaller med multiplikasjoner:

2HCl (g) + 1/2₂(g) → h₂Eller (l) + cl₂(g) (ΔH = -202.4 kJ/mol) * (1/2)

Denne ligningen ble multiplisert med 1/2 for å ha 2HCl i stedet for 4HCl

H₂(g) + f₂(g) → 2HF (L) (ΔH = -600.0 kJ/mol) * (2)

Denne ligningen multiplisert med 2 for å ha f₂ og nr. 1/2f₂

H₂Eller (l) → h₂(g) + 1/2o₂(g) (ΔH = -285.8 kJ/mol) * (-1)

I mellomtiden multipliseres sistnevnte med -1 for å "snu det". Dermed har vi de bestilte ligningene og klare til å legge til.

Sum av ligningene

Å legge til alt gir oss:

2HCl (g) + 1/2₂(g) → h₂Eller (l) + cl₂(g) (ΔH = -101.2 kJ/mol)

H₂(g) + f₂(g) → 2HF (L) ΔH = -1200.0 kJ/mol)

H₂Eller (l) → h₂(g) + 1/2o₂(g) (ΔH = 285.8 kJ/mol)

2HCl (g) + f₂(g) → 2HF (L) +CL₂(g)

Merk at begrepene 1/2₂, H₂Eller og h₂ De blir kansellert fordi de er på begge sider av pilen. Enthalpies legges også til, og gir:

ΔHRX = 285.8 kJ/mol + (-101.2 kJ/mol) + (-1200.0 kJ/mol)

Dette uttrykket er det samme som begynnelsen:

ΔH = ΔH₁ + ΔH₂ + ΔH₃

Og så, vi har at Δhrx er lik:

ΔHRX = -1015.4 kJ/mol

- Eksempel 2

I dette eksemplet vil det sees at entalpiene til de alternative reaksjonene tilsvarer entalpiene om dannelse av interesseforbindelser.

Det er ønsket å bestemme Δhrxn for neste nedbrytningsreaksjon:

2SO₃(g) → 2SO₂(g) + eller₂(g)

Og treningsentalpiene til SO -forbindelsene telles for hånden₃ Og så₂:

S (s) + o₂(g) → Så₂(g) (ΔH = -296.8 kJ/mol)

Kan tjene deg: Isopreno: Struktur, egenskaper, applikasjoner

S (s) + 3/2o₂(g) → Så₃(g) (ΔH = -395.6 kJ/mol)

Ligninger bestilling

Denne øvelsen vil bli løst på samme måte som forrige eksempel. Det skal være slik₃ ha rett, og multipliser med 2. For det må vi "snu" SO -formasjonsligningen₃ multiplisere den med -1, og deretter ved å multiplisere den med 2:

2SO₃(g) → 2s (r) + 3o₂(g) (ΔH = -395.6 kJ/mol) * (-2)

SO -formasjonsligningen₂ Vi multipliserer det også med 2:

2s (S) + 2₂(g) → 2SO₂(g) (ΔH = -296.8 kJ/mol) * (2)

Sum av ligningene

Nå er ligningene lagt til:

2SO₃(g) → 2s (r) + 3o₂(g) (ΔH = 791.2 kJ/mol)

2s (S) + 2₂(g) → 2SO₂(g) (ΔH = -593.6 kJ/mol)

2SO₃(g) → 2SO₂(g) + eller₂(g)

Merk at begrepet 2 er eliminert fordi det er på begge sider av pilen. Også 3. plass₂ 2o trekkes fra₂ gir en o₂. Summen av entalpiene, og derfor vil verdien av Δhrxn være:

ΔH = ΔHrxn = 791.2 kJ/mol + (-593.6 kJ/mol)

= 197.6 kJ/mol

Som enhver nedbrytningsreaksjon er den endotermisk, så dens entalpi er positiv.

Alternativ metode

Det er en metode for å nå samme resultat på en mer direkte og enkel måte. Dette ble nevnt i en tidligere seksjon.

2SO₃(g) → 2SO₂(g) + eller₂(g)

For å bestemme Δhrxn for denne reaksjonen, må vi beregne ΔHºF (reagenser) og ΔHºF (produkter). Δhºf (så₃) er lik -395.6 kJ/mol, mens ΔHºF (så₂) er lik -296.8 kJ/mol. ΔHºF (eller₂) er lik 0, siden elementært oksygen eksisterer som et molekyl av O₂ og ikke som atomer eller gratis.

Så vi har:

ΔHrxn = ΔHºF (produkter) - ΔHºF (reagenser)

= [Δhºf (så₂) + ΔHºF (eller₂)] - ΔHºF (så₃)

= Δhºf (så₂) - ΔHºF (så₃)

Vi må imidlertid multiplisere begge treningsentalpiene med 2, for å matche de støkiometriske koeffisientene med hensyn til den kjemiske ligningen:

ΔHrxn = 2ΔHºF (så₂) - 2ΔHºF (så₃)

Og beregning vi har:

ΔHrxn = 2 (-296.8 kJ/mol) - 2 (-395.6 kJ/mol)

= 197.6 kJ/mol

Dette er faktisk måten det vanligvis foretrekkes å løse alle øvelsene som Hess -loven blir anvendt.

Referanser

1. Whitten, Davis, Peck & Stanley. (2008). Kjemi. (8. utg.). Cengage Learning.
2. Wikipedia. (2020). Hess's lov. Hentet fra: i.Wikipedia.org
3. Cohen Shelly. (18. mai 2020). Hess's lov. Kjemi librettexts. Gjenopprettet fra: Chem.Librettexts.org
4. Clark Jim. (2010). Hess's lov og entalpi endrer beregninger. Gjenopprettet fra: Chemguide.co.Storbritannia
5. Helmestine, Anne Marie, PH.D. (11. februar 2020). Hess's lovdefinisjon. Gjenopprettet fra: Thoughtco.com
6. Foist Laura. (2020). Hess's Law: Definisjon, formel og eksempel. Studere. Gjenopprettet fra: Studie.com
7. Quimitube. (2014). Teori 14 Termokjemi: Beregning av entalpien av en reaksjon etter Hess's lov. Gjenopprettet fra: Quimitube.com