Signerer lov

Vi forklarer loven om tegn, med eksempler og øvelser løst

Ordningen for tegnloven

Hva er loven om tegn?

De Signerer lov Det er settet med regler som brukes i aritmetiske og algebraiske beregninger med reelle tall for å tilordne tegnet riktig til resultatet, når både positive og negative mengder er involvert.

Det er tilstrekkelige regler i henhold til operasjonen som utføres: sum, subtraksjon, multiplikasjon og divisjon, som er de mest grunnleggende, og det er også regler for tegn relatert til potensiering og arkiveringsoperasjon.

I en gitt operasjon, enten det er for hånd eller med kalkulator, er det nødvendig å anvende loven til skiltene riktig for å sikre et riktig resultat, siden bare en liten endring i skiltene betydelig endrer beløpene.

Loven for tegnene for hver grunnleggende aritmetisk operasjon og sakene som kan oppstå blir undersøkt nedenfor.

Lov om tegn på sum

1) Hvis tallene som skal legges til, har samme tegn

Tallene legges til som vanlig, og resultatet legges til tegnet på tallene, uavhengig av om dette er positivt eller negativt.

Det er viktig å huske på at positive tall vanligvis ikke er før skiltet, men skrives direkte. På den annen side er negative tall skrevet i parenteser, spesielt når de er gitt av symbolet på en aritmetisk operasjon, for å unngå forvirring.

Eksempler på summer av tall med samme tegn:

3 + 9 = 12
4 + 7 + 1 + 6 = 18
(−3) + (−8) = −11
(−5) + (−10) + (−6) = −21

2) Hvis tallene som skal legges til, har forskjellige tegn

Tallene trekkes fra og tegnet på antallet som har den største absolutte verdien legges til resultatet, enten det er positivt eller negativt.

Som et eksempel, utfør operasjon 5 + (−14). Ettersom den absolutte verdien av (−14) er større enn den absolutte verdien på 5, trekkes 5 enheter fra 14, noe som gir 9 og dette resultatet er plassert negativt tegn:

Kan tjene deg: Prismer og pyramider

5 + (−14) = −9

Flere eksempler på denne regelen som brukes på summen av to antall forskjellige tegn er:

(−27) + 12 = −15

12 + (−7) = 5

Hvis det er i operasjonen er det mer enn to tillegg med forskjellige tegn, Assosiativ eiendom av summen:

(−20) + 9 + (−7) = [(−20) + 9] + (−7)

Operasjonen utføres først i Pracete, som består av summen av to antall forskjellige tegn, som den beskrevne regelen brukes: Resultatet trekkes fra og tegnet på tallet med den høyeste absolutte verdien:

(−20) + 9 = −11

Operasjonen er slik:

(−20) + 9 + (−7) = (−11) + (−7)

Nå har du summen av to antall av det samme tegnet, så blir de normalt lagt til og resultatet plasseres et negativt tegn:

(−20) + 9 + (−7) = (−11) + (−7) = −18

Tegn i erstatningen

Subtraksjon av to tall er definert som summen av det motsatte. På sin side er det motsatte av et nummer sagt nummer med det endrede tegnet. For eksempel er det motsatte av 2 (−2), det motsatte av (−5) er 5 og så videre.

Med dette i bakhodet, når du har subtraksjon av to tall:

A - b

Det forvandles rett og slett til summen av det motsatte av B:

A + ( - b)

Og fortsett som beskrevet i forrige seksjon. Merk for å sette et tegn + et negativt tall endrer det ikke, men veldig forsiktig, det motsatte er ikke sant.

Når tallet "A", som er minuend, er større enn antallet "B", som er stjålet, fungerer som i subtraksjon av naturlige tall. Ikke noe problem, siden et stort antall trekkes fra et mindre beløp:

Kan tjene deg: ulikhet i trekanten: demonstrasjon, eksempler, løste øvelser

25 - 8 = 17

Med følgende eksempler er metoden for å legge det motsatte til å trekke fra veldig praktisk:

(−5) - 24 = (−5) +( - 24) = - 29
32 - (−23) = 32 + 23 = 55

Lov om tegn i multiplikasjon

Loven for tegnene i multiplikasjon brukes på denne måten:

• Ved å multiplisere to tall med samme tegn, er resultatet alltid positivt.
• Produktet av to motsatte skiltnummer er alltid negativt.

Sammendraget av tegnregelen for multiplikasjon vises på bildet:

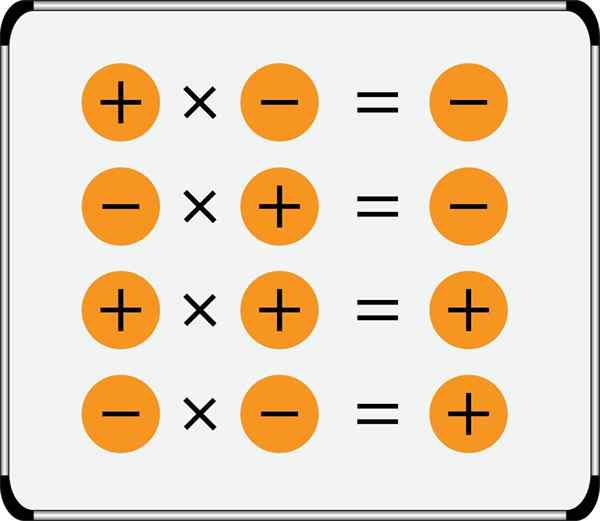
Legg merke til at positive tall kan skrives uten foregående tegn, men negative tall har det alltid, i tillegg, to aritmetiske symboler blir aldri skrevet til hverandre, de må alltid skilles med en parentes, for eksempel:

Stemmer ikke: 3 × −4
Riktig: 3 × (−4) = −12

(−5) × 6 = −5 × 6 = −30
(−3) × (−11) = 33
10 × 27 = 270

For å multiplisere mer enn to tall, brukes den assosiative egenskapen til multiplikasjon, siden rekkefølgen på faktorene ikke endrer produktet, for eksempel når du utfører:

(−2) × (−14) × 16

Du kan multiplisere de to første faktorene, eller de to siste hvis du vil, og deretter multiplisere resultatet med den gjenværende faktoren. I dette tilfellet vil de to faktorene bli multiplisert først fra venstre:

[(−2) × (−14)] × 16

Produktet av to negative tall er positivt, deretter (−2) × (−14) = 28 og gjenstår:

28 × 16 = 448

Lov om tegn i divisjon

Det er analogt med tegnens regel for multiplikasjon:

• Forholdet mellom to antall av det samme tegnet er alltid positivt.
• Ved å dele to ellers tegnnummer, er resultatet alltid negativt.

Det kan tjene deg: forskjell mellom sirkel og omkrets (med eksempler)

For eksempel:

24 ÷ 8 = 3
−36 ÷ 3 = −12
162 ÷ (−9) = −18
−216 ÷ (−6) = 36

Lov om tegn i empowerment og innlevering

En skriftlig nummereksponent er:

tilⁿ

Hvor "a" er basen og "n" er eksponenten. To tilfeller skilles ut, i henhold til eksponentens paritet:

Sak 1: A er positivt

Når basen er positiv, er resultatet positivt uavhengig av om eksponenten er jevn eller merkelig, som i:

2³ = 8
3⁴ = 81

Sak 2: A er negativ

Her er to tilfeller:

• Når eksponenten er jevn, er resultatet positivt.
• Hvis eksponenten er merkelig, er den negativ.

Eksempler

3² = 3 ∙ 3 = 9
2³ = 2 ∙ 2 ∙ 2 = 8
(−2)⁴ = (−2) ∙ (−2) ∙ (−2) ∙ (−2) = 16
(−3)³ = (−3) ∙ (−3) ∙ (−3) = −27

Operasjoner med grupperingssymboler

De vises ofte separate operasjoner med grupperingssymboler: parentes, parentes og nøkler. Disse elimineres fra innsiden og tar hensyn til følgende:

• Hvis et grupperingssymbol er gitt et positivt tegn, kan det fjernes uten å endre tegn på innholdet, for eksempel: + (−3 + 5 - 1) = −3 + 5 - 1 = 1.
• Hvis et negativt tegn går foran gruppesymbolet, trekkes det tilbake ved å investere tegnet på innholdet, for eksempel: - (−3 + 5 −1) = 3 - 5 + 1 = −1.
• Når det er kombinert drift av sum, subtraksjon, multiplikasjon og inndeling, kan de assosiative og distribusjonsegenskapene brukes til bekvemmelighet.

Løste øvelser

a) 10 + 10

Løsning: 20

b) (-8) + (-3)

Løsning: -11

c) (3) + (-10) 

Løsning: -7

d) (5) x (-3)

Løsning: -15

e) (-10) x (-10)

Løsning: 100

f) (18) ÷ (-3)

Løsning: -6

G) (-10) ÷ (-2)

Løsning: 5

h) 4 - ( - 7 + 9)

Løsning: 4 - ( - 7 + 9) = 4 + 7 - 9 = 11− 9 = 2