Sandwich lovforklaring og øvelser

De Sandwich Law eller tortilla er en metode som gjør det mulig å operere med brøk; Spesifikt lar det deg dele brøk. Med andre ord, gjennom denne loven kan du gjøre rasjonelle tallavdelinger. Sandwichs lov er et nyttig og enkelt verktøy å huske.

Denne artikkelen vil bare bli betraktet som tilfellet med inndeling av rasjonelle tall som ikke begge er hele tall. Disse rasjonelle tallene er også kjent som brøk eller ødelagte tall.

Forklaring

Anta at du må dele to brøknummer a/b ÷ c/d. Sandwich -loven består i å uttrykke denne divisjonen som følger:

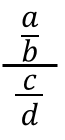
Denne loven slår fast at resultatet oppnås ved å multiplisere antallet som ligger i øvre ende (i dette tilfellet tallet "a") med det nedre endenummeret (i dette tilfellet "d"), og dele denne multiplikasjonen mellom produktet av den Middels tall (i dette tilfellet "B" og "C"). Dermed er den forrige divisjonen lik × d/b × c.

Det kan observeres i veien for å uttrykke den forrige divisjonen at mediumlinjen er lengre enn for brøkdeler. Det er også verdsatt at det ligner på en sandwich, siden tapasene er brøkdelene du vil dele.

Denne divisjonsteknikken er også kjent som Double C, siden en stor “C” kan brukes til å identifisere produktet av ekstreme tall og en mindre “C” for å identifisere produktet av mediumtallene:

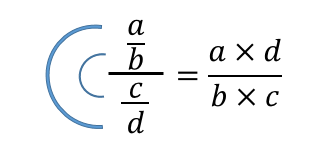
Illustrasjon

Fraksjonelle eller rasjonelle tall er tall på M/N -formen, der "M" og "N" er hele tall. Den multiplikative inverse av et rasjonelt tall M/N består av et annet rasjonelt tall som ved å multiplisere det med M/N resulterer i nummer én (1).

Denne multiplikative inverse er betegnet med (m/n)^-1 Og det er lik n/m, siden m/n × n/m = m × n/n × m = 1. Ved notasjon må du også (m/n)^-1= 1/(m/n).

Den matematiske begrunnelsen av sandwichloven, så vel som andre eksisterende teknikker for å dele opp brøk, ligger i det faktum at ved å dele to rasjonelle tall A/B og C/D, i bakgrunnen det som gjøres er multiplikasjonen av A/B for den multiplikative inverse av C/D. Dette er:

A/b ÷ c/d = a/b × 1/(c/d) = a/b × (c/d)^-1= a/b × d/c = a × d/b × c, som tidligere oppnådd.

For ikke å jobbe mer, er noe som må tas i betraktning før du bruker loven i smørbrødet at begge brøkene er så forenklet som mulig, siden det er tilfeller der det ikke er nødvendig å bruke loven.

For eksempel 8/2 ÷ 16/4 = 4 ÷ 4 = 1. Loven om smørbrødet kunne ha blitt brukt, og oppnådd det samme resultatet etter å forenkle.

En annen viktig ting å vurdere er at denne loven også kan brukes når et brøknummer kreves av et heltall. I dette tilfellet må en 1 plasseres under heltallet, og fortsette å bruke loven om smørbrødet som før. Dette er fordi ethvert hele tall k oppfyller at k = k/1.

Øvelser

Nedenfor er en serie divisjoner der sandwichens lov brukes:

• 2 ÷ (7/3) = (2/1) ÷ (7/3) = (2 × 3)/(1 × 7) = 6/7.
• 2/4 ÷ 5/6 = 1/2 ÷ 5/6 = 1 × 6/2 × 5 = 6/10 = 3/5.

I dette tilfellet ble brøk 2/4 og 6/10 forenklet, og delte mellom 2 opp og ned. Dette er en klassisk metode for å forenkle brøk som består av å finne de vanlige delingene til telleren og nevneren (hvis noen) og dele både mellom den vanlige divisoren til en irreducible brøkdel er oppnådd (hvor det ikke er noen vanlige delere).

• (xy+y)/z ÷ (x+1)/z²= (xy+y) z²/z (x+1) = (x+1) yz²/z (x+1) = yz.

Referanser

1. Almaguer, g. (2002). Matematikk 1. Redaksjonell Limusa.
2. Álvarez, J., Jácome, J., López, J., Cruz, e. d., & Tetumo, j. (2007). Grunnleggende matematikk, støtteelementer. Univ. J. Autonomous of Tabasco.
3. Bails, f. (1839). Prinsipper for aritmetikk. Trykt av Ignacio oppfylt.
4. Barker, l. (2011). Levede tekster for matematikk: Antall og operasjoner. Lærer skapte materialer.
5. Barrios, a. TIL. (2001). Matematikk 2. Redaksjonell progreso.
6. Eguiluz, m. L. (2000). Fraksjoner: en hodepine? Romanbøker.