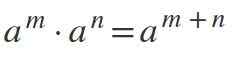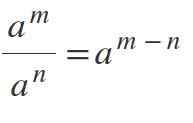Lover for eksponentene

Hva er eksponentlovene?

De Lover for eksponentene De er de som gjelder for dette tallet som indikerer hvor mange ganger et basenummer må multipliseres av seg selv. Eksponenter er også kjent som krefter. Potensieringen er en matematisk operasjon dannet av en base (a), eksponenten (m) og kraften (b), som er resultatet av operasjonen.

Eksponenter brukes vanligvis når veldig store mengder brukes, fordi dette ikke er noe mer enn forkortelser som representerer multiplikasjonen av det samme antallet en viss mengde ganger. Eksponenter kan være både positive og negative.

Hva er eksponenter i matematiske operasjoner?

Som nevnt ovenfor, er eksponenter en forkortet form som representerer multiplikasjonen av tall for seg selv, der eksponenten bare gjelder venstre nummer. For eksempel:

2³ = 2*2*2 = 8

I så fall er nummer 2 basen for kraften, som vil bli multiplisert 3 ganger som indikert av eksponenten, som ligger i øverste høyre hjørne av basen. Det er forskjellige måter å lese uttrykket på: 2 forhøyet til 3 eller 2 hevet til kuben.

Eksponentene indikerer også antall ganger som kan deles, og for å skille denne operasjonen fra multiplikasjonen har eksponenten minus (-) tegnet foran seg selv (det er negativt), noe som betyr at eksponenten er i nevneren av en brøkdel. For eksempel:

2^{- 4} = 1/2*2*2*2 = 1/16

Dette skal ikke forveksles med saken der basen er negativ, siden det vil avhenge av om eksponenten er jevn eller merkelig å avgjøre om kraften vil være positiv eller negativ. Dermed må du:

- Hvis eksponenten er jevn, vil kraften være positiv. For eksempel:

(-7)² = -7 _* -7 = 49.

- Hvis eksponenten er merkelig, vil kraften være negativ. For eksempel:

(-2)⁵ = (-2)*(-2)*(-2)*(-2)*(-2) = -32.

Det er et spesielt tilfelle der hvis eksponenten er lik 0, er kraften lik 1. Det er også muligheten for at basen er 0; I så fall, avhengig av eksponenten, vil kraften være ubestemt eller ikke.

For å utføre matematiske operasjoner med eksponenter er det nødvendig.

Hva er eksponentlovene?

Første lov: Eksponentkraft lik 1

Når eksponenten er 1, vil resultatet være den samme verdien som basen: a¹ = a.

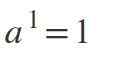
Eksempler

9¹ = 9.

22¹ = 22.

895¹ = 895.

Andre lov: Eksponentkraft lik 0

Når eksponenten er 0, hvis basen er forskjellig fra null, vil resultatet være: a⁰ = 1.

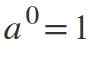
Eksempler

1⁰ = 1.

323⁰= 1.

1095⁰ = 1.

Tredje lov: negativ eksponent

Ettersom eksponenten er negativ, vil resultatet være en brøkdel, der kraften vil være nevneren. For eksempel, hvis M er positiv, da^-m = 1/a^m.

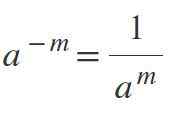
Eksempler

- 3^-1 = 1/3.

- 6^-2 = 1/6² = 1/36.

- 8^-3 = 1/8³ = 1/512.

Fjerde lov: Multiplikasjon av like krefter med det samme

For å multiplisere krefter der basene er de samme og forskjellige fra 0, opprettholdes basen og eksponentene legges til: a^m _* tilⁿ = a^m+n.    

Eksempler

- 4⁴ _* 4³ = 4⁴⁺³ = 4⁷

- 8¹ _* 8⁴ = 8¹⁺⁴ = 8⁵

- 2² _* 2⁹ = 2²⁺⁹ = 2^elleve

Femte lov: Power Division med samme base

For å dele krefter der basene er de samme og forskjellige fra 0, opprettholdes basen og eksponentene trekkes fra som følger: a^m / tilⁿ = a^M-n.    

Eksempler

- 9² / 9¹ = 9 ^(tjueen) = 9¹.

- 6^femten / 6¹⁰ = 6 ^{(15 - 10)} = 6⁵.

- 49¹² / 49⁶ = 49 ^{(12 - 6)} = 49⁶.

Sjette lov: Multiplikasjon av forskjellige krefter med en annen base

I denne loven er det det motsatte av det som kommer til uttrykk i det fjerde; Det vil si at hvis du har forskjellige baser, men med de samme eksponentene, multipliseres basene og eksponenten opprettholdes: a^m _* b^m = (a_*b) ^m.

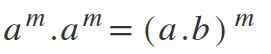
Eksempler

- 10² _* tjue² = (10 _* tjue)² = 200².

- Fire fem^elleve _* 9^elleve = (45*9)^{11 =} 405^elleve.

En annen måte å representere denne loven er når en multiplikasjon er høy til en makt. Dermed vil eksponenten tilhøre hvert av vilkårene: (a_*b)^m= a^m_* b^m.

Eksempler

- (5_*8)⁴ = 5⁴ _* 8⁴ = 40⁴.

- (23 * 7)⁶ = 23⁶ _* 7⁶ = 161⁶.

Syvende lov: Different Power Division

Hvis du har forskjellige baser, men med de samme eksponentene, er basene delt og eksponenten opprettholdes:^m / b^m = (a / b)^m.

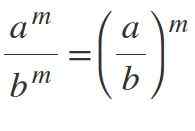
Eksempler

- 30³ / 2³ = (30/2)³ = 15³.

- 440⁴ / 80⁴ = (440/80)⁴ = 5.5⁴.

Tilsvarende, når en divisjon er høy til en makt, vil eksponenten høre til i hvert av vilkårene: (a / b) ^m = a^m /b^m.

Eksempler

- (8/4)⁸ = 8⁸ / 4⁸ = 2⁸.

- (25/5)² = 25² / 5² = 5².

Det er tilfelle der eksponenten er negativ. Så for å være positiv, investeres verdien av telleren med denominatoren, som følger:

- (A / B)^-n = (b / a)ⁿ = bⁿ / tilⁿ.

- (4/5) ^-9 = (5/4) ⁹ = 5⁹ / 4⁴.

Åttende lov: makt av en makt

Når du har en kraft som blir hevet til en annen makt -det er, to eksponenter samtidig -Basen opprettholdes og eksponentene multipliserer: (a^m)ⁿ= a^m*n.

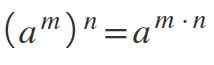
Eksempler

- (8³)² = 8 ^(3*2) = 8⁶.

- (1. 3⁹)³ = 13 ^(9*3) = 13²⁷.

- (238¹⁰)¹² = 238^{(10 * 12)} = 238¹²⁰.

Niende lov: brøkeksponent

Hvis kraften som en eksponent en brøkdel, løses dette ved å transformere den til en N-ESIMA-rot, der telleren forblir som en eksponent og nevneren representerer rotindeksen:

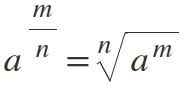
Eksempel

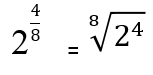
Løste øvelser

Oppgave 1

Beregn operasjonene mellom kreftene som har forskjellige baser:

2⁴ _* 4⁴ / 8².

Løsning

Bruker reglene for eksponentene, basene multipliseres i telleren og eksponenten opprettholdes, slik:

2⁴ _* 4⁴ / 8²= (2_*4)⁴ / 8²  = 8⁴ / 8²

Nå som det er like baser, men med forskjellige eksponenter, opprettholdes basen og eksponentene trekkes fra:

 8⁴ / 8² = 8^{(4 - 2)} = 8²

Oppgave 2

Beregn driften mellom høye krefter til en annen makt:

(3²)³ _* (2 _* 6⁵)^-2 _* (2²)³

Løsning

Bruke lovene, må du:

(3²)³ _* (2 _* 6⁵)^-2 _* (2²)³

= 3⁶ _* 2^-2 _* 2^-10 _* 2⁶

= 3⁶ _* 2^{(-2) + (- 10)} _* 2⁶

= 3⁶ _*  2^-12 _* 2⁶

= 3⁶ _* 2^{(-12) + (6)}

= 3⁶ _* 2⁶

= (3_*2)⁶

= 6⁶

= 46.656

Referanser

1. Aponte, g. (1998). Grunnleggende matematikkfundamentals. Pearson Education.
2. Corbalán, f. (1997). Matematikk gjaldt hverdagen.
3. Jiménez, J. R. (2009). Matematikk 1 september.
4. Max Peters, w. L. (1972). Algebra og trigonometri.
5. Rees, p. K. (1986). REVERTE.