Blokker algebraelementer, eksempler, øvelser løst

Han Blokk algebra Det refererer til settet med operasjoner som utføres gjennom blokker. Disse og noen flere elementer tjener til å skjematisk representere et system og enkelt visualisere svaret ditt på en spesifikk oppføring.

Generelt inneholder et system forskjellige elektriske, elektroniske og elektromekaniske elementer, og hver av dem, med sin respektive funksjon og plassering i systemet, så vel som måten de er relatert, blir skjematisert gjennom funksjonelle blokker.

Figur 1.

I figuren over er det et veldig enkelt system, som består av et inngangssignal x (er), som kommer inn i blokken med overføringsfunksjonen g (s) som endrer det og produserer utgangen y (s).

Det er praktisk å representere signalene og deres reise gjennom systemet gjennom piler som kommer inn og forlater hver blokk. Vanligvis er signalstrømmen rettet fra venstre mot høyre.

Fordelen med denne typen ordninger er den visuelle hjelpen den gir for å forstå systemet, selv om det ikke utgjør en fysisk representasjon av det samme. Faktisk er blokkdiagrammet ikke unikt, for i henhold til synspunktet kan til og med flere diagrammer av det samme systemet trekkes.

Det kan også hende at det samme diagrammet brukes til flere systemer som ikke nødvendigvis er relatert til hverandre, forutsatt at oppførselen beskriver riktig. Det er forskjellige systemer hvis respons er likt i mange aspekter, for eksempel en LC-krets (induktor-kanal) og et masse-resort-system.

[TOC]

Hva er et blokkdiagram?

Systemene er vanligvis mer kompliserte enn for figur 1, men blokkeringsalgebra gir en serie enkle regler for å manipulere systemskjemaet og redusere den til den enkleste versjonen.

Som forklart i begynnelsen, bruker diagrammet blokker, piler og sirkler for å etablere forholdet mellom hver systemkomponent og strømmen av signalene som går gjennom det.

Blokkalgebra gjør det mulig å sammenligne to eller flere signaler gjennom sum, subtraksjon og multiplikasjon av dem, samt analysere bidraget som hver komponent gir til systemet.

Takket være dette er det mulig å redusere hele systemet til et enkelt inngangssignal, en unik overføringsfunksjon som fullstendig beskriver systemvirkningen og den tilsvarende utgangen.

Det kan tjene deg: Astroclymics: Historie, hvilke studier, grener

Blokkerer diagramelementer

Elementene i blokkdiagrammet er følgende:

Signalet

Signalene er veldig varierte, for eksempel er det vanlig at den er en elektrisk strøm eller spenning, men det kan være lys, lyd og mer. Det viktige er at den inneholder informasjon om et bestemt system.

Signalet er betegnet med store bokstaver hvis det er en funksjon av variabelen s av Laplace -transformasjonen: x (er) (se figur 1) eller med små bokstaver hvis det er basert på tid t, som x (t).

I blokkdiagrammet er inngangssignalet representert med en pil rettet mot blokken, mens utgangssignalet, betegnet som y (er) eller (t), er indikert med en utgående pil.

Både inngangs- og utgangssignalet er unikt og adressen som informasjonsstrømmene bestemmes av pilens retning. Og algebra er den samme for en av de to variablene.

Blokken

Blokken er representert med et kvadrat eller et rektangel (se figur 1) og kan brukes til å utføre operasjoner eller implementere overføringsfunksjonen, som vanligvis betegnes med store bokstaver G. Denne funksjonen er en matematisk modell som responsen som tilbys av systemet er beskrevet før et inngangssignal.

Overføringsfunksjonen kan uttrykkes i form av tid t for eksempel g (t) eller variabelen s som g (s).

Når inngangssignalet x (er) kommer til blokken, multipliseres det med overføringsfunksjonen og transformeres til utgangssignalet y (s). Matematisk uttrykkes det som følger:

Og (er) = x (er).G (s)

Tilsvarende er overføringsfunksjonen forholdet mellom Laplace -transformasjonen av utgangssignalet og Laplace -transformasjonen av inngangssignalet, forutsatt at de opprinnelige forholdene til systemet er null:

G (s) = y (s) / x (s)

Sumspunkt

Summen eller sommeren er symbolisert av en sirkel med et kors innvendig. Det brukes til å kombinere, med summer og subtraksjon, to eller flere signaler. På slutten av pilen som symboliserer signalet, plasseres et tegn + direkte hvis det signalet legges til eller et tegn - hvis trukket fra trekket.

I den følgende figuren er det et eksempel på hvordan sommeren fungerer: du har inngangssignalet x, som signalene A og B legges til, og oppnår som et resultat avkjørselen og, som algebraisk tilsvarer:

Kan tjene deg: Vertikal skudd: Formler, ligninger, eksempler

Y = x+a+b

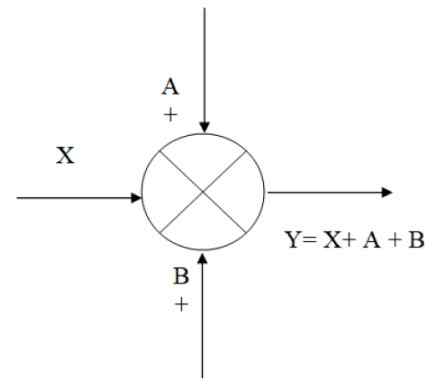Figur 2. Eksempel på en håndhevelse. Kilde: f. Zapata.

Grenpunkt

Det heter også Bifurkasjonspunkt. I det er signalet som kommer ut av en blokk distribuert til andre blokker eller til en plyme. Det er representert av et punkt plassert på pilens pil og en annen pil kommer fra det som omdirigerer signalet mot en annen del.

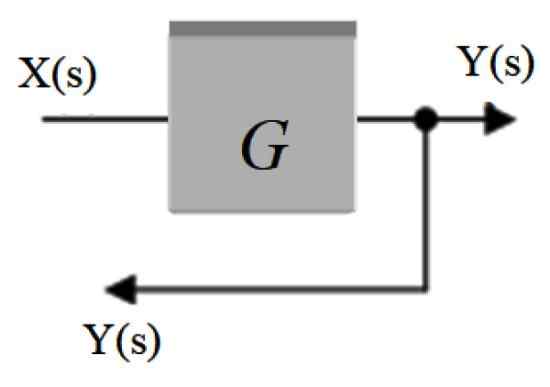Figur 3. Grenpunkt. Kilde: f. Zapata.

Eksempler på blokker av blokkeringsalgebraen

Som forklart før, er ideen å uttrykke systemet gjennom blokkdiagrammet og redusere det for å finne overføringsfunksjonen som beskriver det. Følgende er reglene for blokkeringsalgebraen for å forenkle diagrammer:

Kaskadeblokker

Når du har et signal som passerer suksessivt gjennom G -blokkene₁, G₂, G₃..., den reduseres til en unik blokk hvis overføringsfunksjon er et produkt av g₁, G₂, G₃..

I det følgende eksemplet kommer signal X (er) inn i den første blokken, og dens utgang er:

OG₁(S) = x (s).G₁(S)

Figur 4. To blokker i fossen. Kilde: f. Zapata.

I sin tur og₁(S) Angi G -blokken₂(S), hvis avgang er:

OG₂(S) = x (s).G₁(S). G₂(S)

Prosedyren er gyldig for n kaskadeblokker:

OG_n (S) = x (s). G₁(S).G₂(S) ... g_n(S)

Blokkerer parallelt

I venstre diagram signaliserer X (S) Bifurca for å legge inn G -blokkene₁(S) og G₂(S):

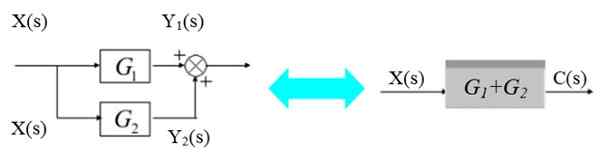Figur 5. To blokker parallelt. Kilde: f. Zapata.

De respektive utgangssignalene er:

OG₁(S) = x (s).G₁(S)

OG₂(S) = x (s).G₂(S)

Disse signalene legges til for å oppnå:

C (s) = y₁(S) +₂(S) = x (s).[G₁(S) + G₂(S)]

Som vist i høyre -riktig diagram.

Flytt en frier til venstre

En sommer kan bevege seg til venstre for blokken som følger:

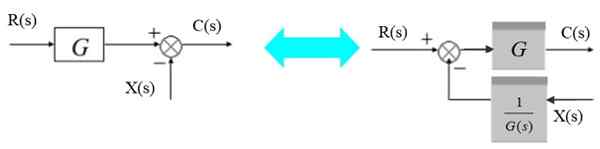Figur 6. Flytt adeksten til venstre for blokken. Kilde: f. Zapata.

Til venstre er utgangssignalet:

C (s) = r (s). G (s) - x (s)

Tilsvarende med høyre:

C (S) = [R (S) - X (S)/G (S)]].G (s)

Flytt en høyre til høyre

Sommeren kan bevege seg til høyre for blokken slik:

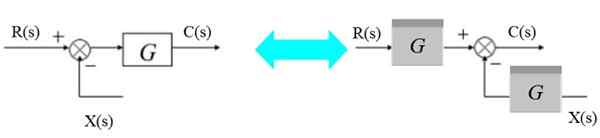Figur 7. Flytt en tomt til høyre for blokken. Kilde: f. Zapata.

På venstre side har du: [r (s) - x (s)].G (s) = c (s)

Kan tjene deg: Archimedes -prinsipp: Formel, demonstrasjon, applikasjoner

Og til høyre:

R (s). G (s) - x (s).G (s) = c (s)

Flytt et bifurkasjonspunkt fra venstre mot høyre

For å fortrenge bifurkasjonspunktet fra venstre til høyre for blokken, er det nok til å observere at utgangen C (S) til høyre er produkt X (S).G (s). Som du vil bli x (er) igjen, multipliseres det med det inverse av g (s).

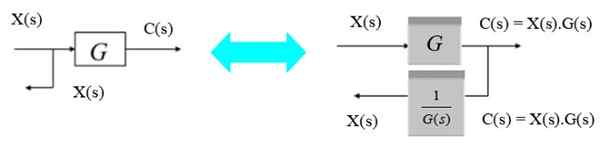Figur 8. Flytt et grenpunkt fra venstre mot høyre. Kilde: f. Zapata.

Flytt et bifurkasjonspunkt fra høyre til venstre

Alternativt kan bifurkasjonspunktet bevege seg fra høyre til venstre som følger:

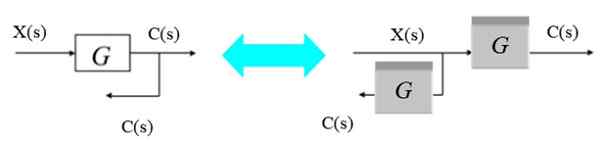Figur 9. Flytt et grenpunkt fra høyre til venstre. Kilde: f. Zapata.

Siden utgangen fra bifurkasjonen ønsker å oppnå C (S), er en ny blokk G (S) ganske enkelt ispedd et bifurkasjonspunkt til venstre for den opprinnelige blokken.

System med tilbakemelding

I det følgende systemet fører utgangssignalet C (S) gjennom det underdanige til venstre:

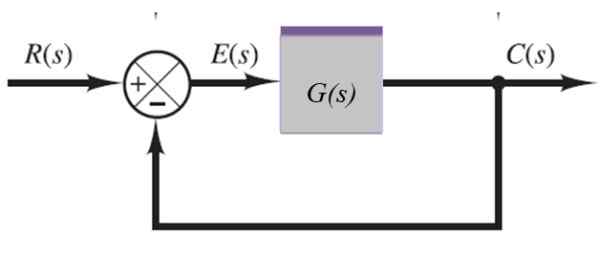Figur 10. System med tilbakemelding. Kilde: f. Zapata.

C (S) = E (S).G (s)

Men:

E (S) = R (S) -C (S)

Å erstatte dette uttrykket i den forrige ligningen er: C (S) = [R (S) -C (S)]].G (s), hvorfra C (er) kan tømmes:

C (S) + C (S).G (s) = r (s).G (s) → c (s). [1 + g (s)] = r (s).G (s)

C (s) = r (s).G (s) / [1 + g (s)]

Eller vekselvis:

C (S) / R (S) = G (S) / [1 + G (S)]]

Grafisk, etter å ha forenklet det er:

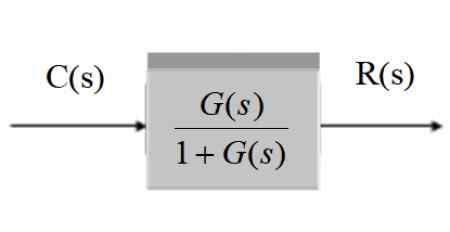Figur 11. Forenkling av et system med tilbakemelding. Kilde: f. Zapata.

System med tilbakemelding og svinger

Transduseren består av overføringsfunksjonen H (er):

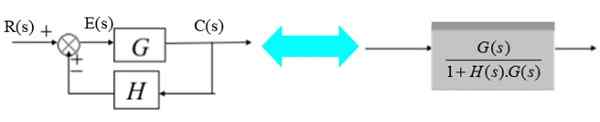Figur 12. System med tilbakemelding og svinger. Kilde: f. Zapata.

I høyre diagram er utgangssignalet C (S):

C (S) = E (S). G (s) med e (s) = r (s) - c (s).H (s)

Så:

C (S) = [R (S) - C (S). H (S)]. G (s)

C (S) [1+ H (S).G (s)] = r (s).G (s)

Derfor kan C (er) tømmes av:

C (s) = g (s).R (s) / [1+ h (s).G (s)]

Og overføringsfunksjonen vil være:

G (s) / [1+ h (s).G (s)]

Som vist i det forenklede høyre diagrammet.

Løste øvelser

Oppgave 1

Finn overføringsfunksjonen til følgende system:

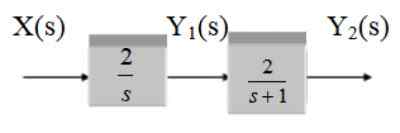Figur 13. To blokkeringssystem i fossen. Kilde: f. Zapata.

Løsning

Det er to kaskadeblokker, derfor er overføringsfunksjonen produktet av funksjonene g₁ og g₂.

Du må:

G₁ = 2/s

G₂ = 2 /(s+1)

Derfor er den etterspurte overføringsfunksjonen:

G (s) = 4 / [s (s+1)]

Oppgave 2

Reduser følgende system:

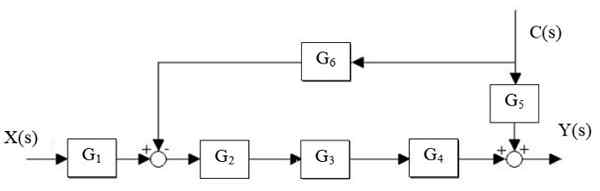Figur 14. Forenkling av et system. Kilde: f. Zapata.

Løsning

Først reduseres G -kaskaden₂, G₃ og g_4, Og den parallelle g skilles₅ og g₆:

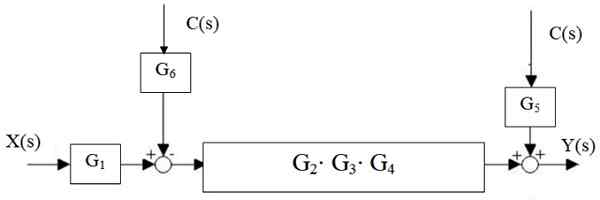Figur 15. Sentral fossefallsreduksjon. Kilde: f. Zapata.

Deretter frieren til venstre for G -blokken₂ ⋅g₃ ⋅ g₄ Han beveger seg til høyre:

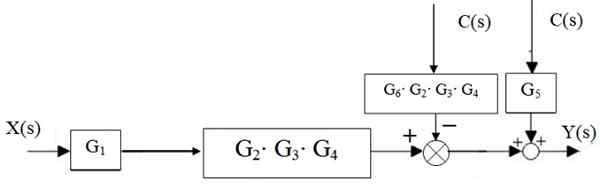Figur 16. Overføring av administratoren. Kilde: f. Zapata.

Somrene til høyre reduseres til en, så vel som kaskadeblokkene:

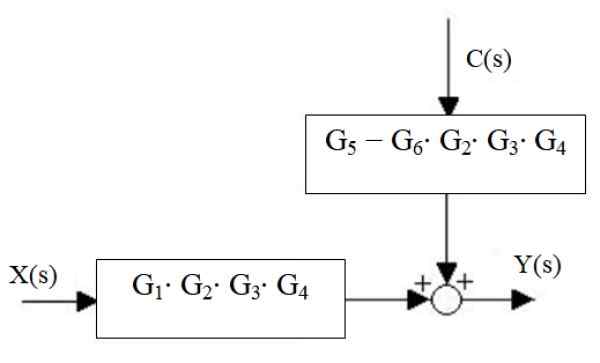Figur 17. Reduksjon av den nye fossen og Summers of the Right. Kilde: f. Zapata.

Endelig er systemutgangen:

Og (er) = x (er) ⋅g₁⋅ g₂ ⋅g₃ ⋅ g₄ + C (S) ⋅ [G₅ - G₆ ⋅ g₂ ⋅g₃ ⋅ g₄]

Referanser

1. Alaydi, J. Systemblokkdiagramkontroll. Gjenopprettet fra: nettstedet.Iugaza.Edu.$.
2. Bolton, w. 2006. Kontrollteknikk. 2. Utgave. Alpha Omega.
3. Cwalinsky, J. Introduksjon til systemblokk algebra. Gjenopprettet fra: Cedengineering.com.
4. DademuchConnection. Blokkerer diagram. Gjenopprettet fra: Dademuch.com.
5. Ogata, k. 2010. Moderne kontrollteknikk. 5. plass. Utgave. Pearson.