Vektoralgebra

Hva er vektoralgebraen?

Han Vektoralgebra Det er en gren av matematikk som har ansvaret for å studere systemer for lineære ligninger, vektorer, matriser, vektorrom og deres lineære transformasjoner. Det er relatert til områder som prosjektering, oppløsning av differensialligninger, funksjonell analyse, operasjonsforskning, beregningsgrafikk, blant andre.

Et annet av områdene som den lineære algebraen har tatt i bruk er fysikk, siden det gjennom dette har vært mulig å utvikle studiet av fysiske fenomener, og beskriver dem gjennom bruk av vektorer. Dette har muliggjort en bedre forståelse av universet.

Grunnleggende

Vektoralgebra stammet fra studiet av kvartærene (utvidelsen av de reelle tallene) 1, I, J og K, samt den kartesiske geometrien som ble fremmet av Gibbs og Heaviside, som innså at vektorene ville tjene som et instrument for å representere Flere fysiske fenomener.

Vektoralgebra studeres gjennom tre fundamenter:

Geometrisk

Vektorer er representert med linjer som har en orientering, og operasjoner som sum, subtraksjon og multiplikasjon med reelle tall er definert gjennom geometriske metoder.

Analytisk

Beskrivelsen av vektorene og deres operasjoner utføres med tall, kalt komponenter. Denne typen beskrivelse er resultatet av en geometrisk representasjon fordi et koordinatsystem brukes.

Aksiomatisk

En beskrivelse av vektorene er laget, uavhengig av koordinatsystem eller av enhver type geometrisk representasjon.

Studien av figurer i verdensrommet gjøres gjennom sin representasjon i et referansesystem, som kan være i en eller flere dimensjoner. Blant hovedsystemene er:

• Unidimensjonalt system, At det er en linje der et punkt (OR) representerer opprinnelsen og et annet punkt (P) bestemmer skalaen (lengden) og retningen til dette:

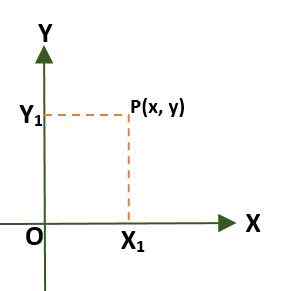
• Rektangulært koordinatsystem (to -dimensjonal), som er sammensatt av to vinkelrett linjer kalt x og y -akse, som passerer gjennom et punkt (eller) opprinnelse; På denne måten er planen delt inn i fire regioner kalt kvadranter. I dette tilfellet er et punkt (p) i flyet gitt av avstandene som eksisterer mellom aksene og p.

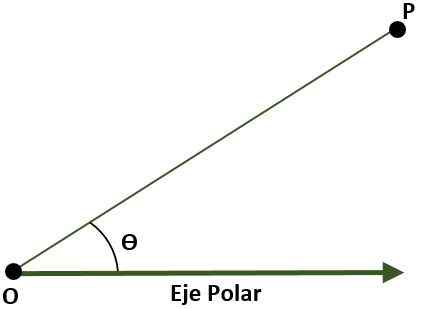
• Polartkoordinatsystem (todimensjonal). I dette tilfellet er systemet sammensatt av et punkt O (opprinnelse) som kalles stolpe og en semi -striver med opprinnelse i eller kalt polarakse. I dette tilfellet er punkt P for planet, med henvisning til polen og polaraksen, gitt av vinkelen (ɵ), som dannes av avstanden mellom opprinnelsen og punktet P.

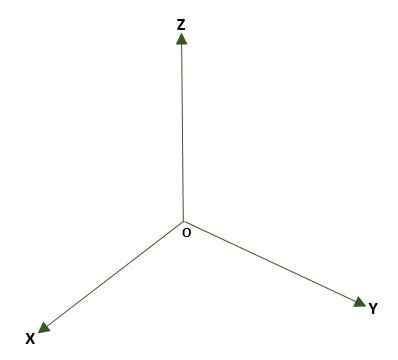
• Rektangulært tre -dimensjonalt system, dannet av tre vinkelrett linjer (x, y, z) som har som poeng eller i rommet. Det dannes tre koordinatfly: XY, XZ og YZ; Plassen vil bli delt inn i åtte regioner kalt Octants. Henvisningen til et punkt P av rommet er gitt av avstandene som finnes mellom flyene og P.

Størrelser

En størrelse er en fysisk mengde som kan telles eller måles gjennom en numerisk verdi, som i tilfelle av noen fysiske fenomener; Imidlertid er det ofte nødvendig å beskrive disse fenomenene med andre faktorer som ikke er numeriske. Det er grunnen til at størrelsene er klassifisert i to typer:

Skalarstørrelse

De er de beløpene som er definert og representerer på en numerisk måte; det vil si av en modul sammen med en måleenhet. For eksempel:

A) Tid: 5 sekunder.

b) Masse: 10 kg.

c) Volum: 40 ml.

D) Temperatur: 40 ºC.

Vektorstørrelse

De er de beløpene som er definert og representert av en modul sammen med en enhet, så vel som av en sans og retning. For eksempel:

Kan tjene deg: Symbolisering av uttrykk

a) Hastighet: (5ȋ - 3ĵ) m/s.

b) akselerasjon: 13 m /s²; S 45º e.

c) Kraft: 280 N, 120º.

d) Vekt: -40 ĵ kg -f.

Vektorstørrelser er grafisk representert av vektorer.

Hva er vektorer?

Vektorer er grafiske representasjoner av en vektorstørrelse; det vil si at de er linjesegmenter der den endelige enden er spissen av en pil.

Disse bestemmes av dens modul eller lengde på segmentet, deres sans som er indikert med spissen av pilen og dens retning i henhold til linjen den tilhører. Opprinnelsen til en vektor er også kjent som søknadspunktet.

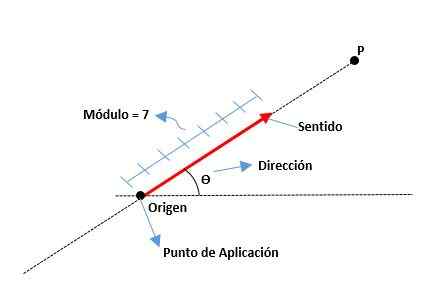
Elementene i en vektor er følgende:

Modul

Det er avstanden fra opprinnelsen til enden av en vektor, representert med et reelt tall sammen med en enhet. For eksempel:

| Om | = | A | = A = 6 cm

Adresse

Det er målet på vinkelen som eksisterer mellom x -aksen (fra den positive) og vektoren, så vel som kardinalpunktene (nord, sør, øst og vest) brukes også.

Føle

Det er gitt av pilspissen som ligger på slutten av vektoren, noe som indikerer hvor dette er rettet.

Klassifisering av vektorer

Generelt klassifiseres vektorer som:

Fast vektor

Det er den hvis applikasjonspunkt (opprinnelse) er fast; det vil si at det forblir knyttet til et rom i rommet, så det kan ikke bevege seg i dette.

Gratis vektor

Den kan bevege seg fritt i verdensrommet fordi opprinnelsen beveger seg til et hvilket som helst punkt uten å endre modulen, betydningen eller retningen.

Skyve vektor

Det er en som kan overføre sin opprinnelse langs sin handlingslinje uten å endre modulen, betydningen eller retningen.

Vektoregenskaper

Blant hovedegenskapene til vektorene er følgende:

Utstyrsvektorer

De er de gratis vektorene som har samme modul, retning (eller disse er parallelle) og sans som en skyvevektor eller en fast vektor.

Tilsvarende vektorer

Det oppstår når to vektorer har samme adresse (eller er parallelle), den samme sansen, og til tross for at de har forskjellige moduler og applikasjonspunkter, forårsaker de like effekter.

Vektor likhet

Disse har samme modul, retning og sans, selv når utgangspunktet er forskjellige, noe som gjør at en parallell vektor kan bevege seg til seg selv uten å påvirke den.

Motsatte vektorer

De er de som har samme modul og retning, men betydningen deres er motsatt.

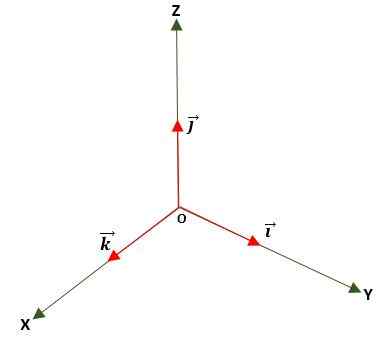
Enhetsvektor

Det er en der modulen er lik enheten (1). Dette oppnås ved å dele vektoren med modulen og brukes til å bestemme retningen og retningen til en vektor, enten i planet eller i rommet, ved bruk av standardiserte base- eller enhetsvektorer, som er:

Nullvektor

Det er den hvis modulen er lik 0; det vil si at dets opprinnelsespunkt og ekstrem sammenfaller på samme punkt.

Vektorkomponenter

Komponentene i en vektor er disse verdiene til vektorprojeksjonene på aksene til referansesystemet; Avhengig av nedbrytning av vektoren, som kan være i akser på henholdsvis to eller tre dimensjoner, vil det oppnås to eller tre komponenter.

Komponentene i en vektor er reelle tall, som kan være positive, negative eller til og med null (0).

På denne måten, hvis du har en ā -vektor, med opprinnelse i et rektangulært koordinatsystem i XY (to -dimensjonalt) plan, er projeksjonen på x -aksen āx og projeksjonen på y -aksen og er āy. Dermed vil vektoren uttrykkes som summen av komponentvektorene.

Eksempler

Første eksempel

Du har en ā -vektor som starter fra opprinnelsen og koordinatene til endene er gitt. Dermed vektoren ā = (ā_x; TIL_og) = (4; 5) cm.

Kan tjene deg: 120 delinger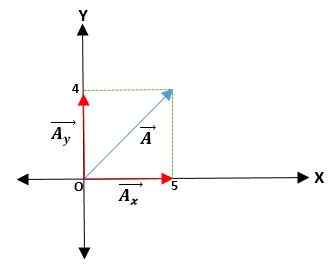

Hvis vektoren ā virker ved opprinnelsen til et tredimensjonalt trekantet koordinatsystem (i rommet) x, y, z, til et annet punkt (p), vil projeksjonene på aksene deres være āx, āy og āz; Dermed vil vektoren uttrykkes som summen av de tre komponentvektorene.

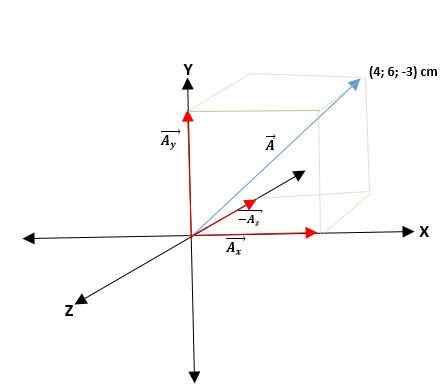
Andre eksempel

Du har en ā -vektor som starter fra opprinnelsen og koordinatene til endene er gitt. Dermed vektoren ā = (a_x; TIL_og; TIL_z) = (4; 6; -3) cm.

Vektorer som har sine rektangulære koordinater kan uttrykkes i henhold til basevektorene. For det må bare hver koordinat multipliseres med dens respektive enhetsvektor, slik at de for planet og rommet vil være følgende:

For flyet: ā = a_xi +a_ogJ.

For plass: ā = a_xi +a_ogJ+a_zk.

Operasjoner med vektorer

Det er mange størrelser som har modul, mening og retning, for eksempel akselerasjon, hastighet, forskyvning, kraft, blant andre.

Disse brukes på forskjellige vitenskapsområder, og for å anvende dem er det i noen tilfeller nødvendig å utføre operasjoner som sum, subtraksjon, multiplikasjon og inndeling av vektorer og skalarer.

Tillegg og subtraksjon av vektorer

Summen og subtraksjon av vektorer regnes som en enkelt algebraisk operasjon fordi subtraksjon kan skrives som en sum; For eksempel kan subtraksjon av vektorer ā og ē uttrykkes som:

Ā - ē = ā + (-ē)

Det er forskjellige metoder for å utføre sum og subtraksjon av vektorer: de kan være grafikk eller analyser.

Grafiske metoder

Brukes når en vektor har en modul, sans og retning. For dette trekkes det linjer som danner en figur som deretter hjelper til med å bestemme det resulterende. Blant de mest kjente er følgende:

Parallellogrammetode

For å lage summen eller subtraksjon av to vektorer, velges et felles punkt på koordinataksen -som vil representere opprinnelsespunktet til vektorene -og opprettholde deres modul, retning og retning.

Deretter trekkes parallelle linjer til vektorene for å danne et parallellogram. Den resulterende vektoren er diagonalen som etterlater fra opprinnelsespunktet til begge vektorene til toppunktet av parallellogrammet:

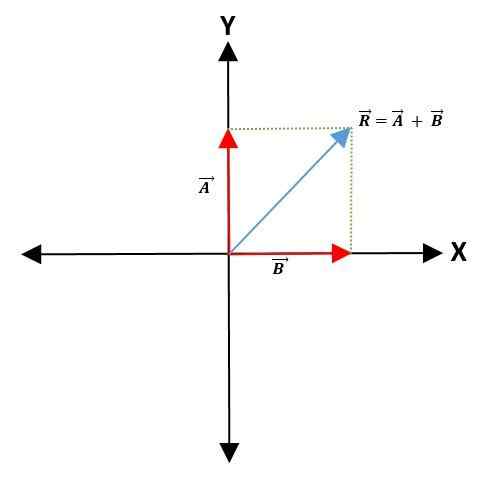
Trekantmetode

I denne metoden plasseres vektorene under den andre, og opprettholder modulene, sansene og adressene sine. Den resulterende vektoren vil være foreningen av opprinnelsen til den første vektoren med slutten av den andre vektoren:

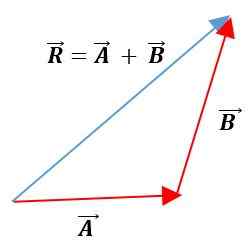
Analytiske metoder

To eller flere vektorer kan legges til eller trekkes gjennom en geometrisk eller vektormetode:

Geometrisk metode

Når to vektorer danner en trekant eller parallellogram, kan M [odulo og retningen til den resulterende vektoren bestemmes ved bruk av lovene i brystet og kosinus. Dermed er den resulterende vektorkodulen, som bruker loven til kosinus og av trekantmetoden, gitt av:

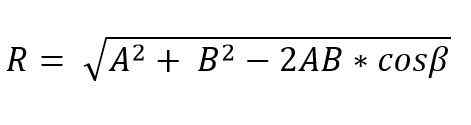
I denne formelen er β motsatt vinkel på R -siden, og dette er lik 180º - ɵ.

På den annen side, ved parallellogrammetoden, er den resulterende vektorkodulen:

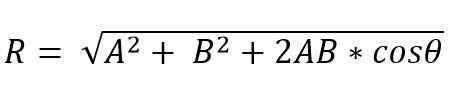
Den resulterende vektoradressen er gitt av vinkel (α), som danner den resulterende med en av vektorene.

Ved brystlov kan summen eller subtraksjon av vektorer også gjøres ved trekanten eller parallellogrammetoden, og vite at sidene i hver trekant er proporsjonale med brystene i de kjekke vinklene:

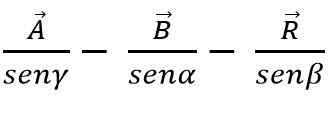
Vektormetode

Dette kan gjøres på to måter: avhengig av dens rektangulære koordinater eller basevektorer.

Vektorene som kommer til å bli lagt til eller trukket mot opprinnelsen til koordinater, kan gjøres, og deretter blir alle fremskrivninger brutt ned i sine rektangulære komponenter i hver av aksene for planet (x, y) eller plass (x, x, og z); Endelig blir komponentene lagt algebraisk. Så for flyet er det:

Kan tjene deg: primo -tall: egenskaper, eksempler, øvelser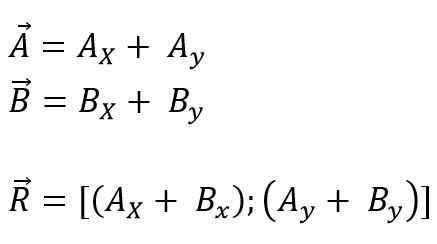

Den resulterende vektorkodulen er:

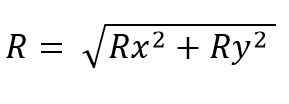
Mens for plass er det:

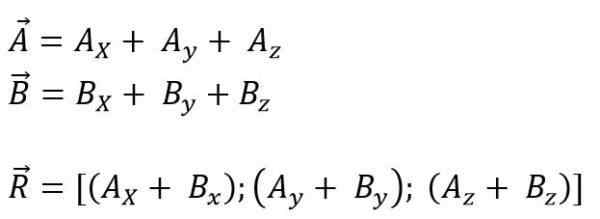
Den resulterende vektorkodulen er:

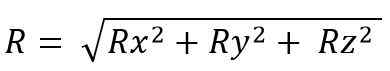
Når vektorsummer blir utført, blir flere egenskaper brukt, som er:

• Assosiativ eiendom: Resultatet endres ikke ved å legge til to vektorer først, og deretter legge til en tredje vektor.
• Kommutativ eiendom: Rekkefølgen på vektorene endrer ikke det resulterende.
• Vektor Distributive eiendom: Hvis en skalar multipliseres med summen av to vektorer, er den lik multiplikasjonen av skalaren for hver vektor.
• Distributiv eiendomsskala: Hvis en vektor multipliseres med summen av to skalarer, er den lik multiplikasjonen av vektoren for hver skalar.

Vektormultiplikasjon

Multiplikasjonen eller produktet av vektorer kan utføres som sum eller subtraksjon, men ved å gjøre det mister den den fysiske betydningen og er nesten aldri innenfor applikasjonene. Derfor er de mest brukte typene produkter skalar- og vektorproduktet.

Skalarprodukt

Det er også kjent som et punkt på to vektorer. Når to -vektormodulene multipliseres med mindre vinkelkosinus som dannes mellom dem, oppnås en skalar. For å uttrykke et skalarprodukt mellom to vektorer er et punkt mellom dem plassert, og dette kan defineres som:

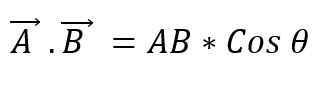
Verdien av vinkelen som eksisterer mellom de to vektorene vil avhenge av om disse er parallelle eller vinkelrett; Dermed må du:

• Hvis vektorene er parallelle og har samme forstand, coseno 0º = 1.
• Hvis vektorene er parallelle og har motsatte sanser, Coseno 180º = -1.
• Hvis vektorene er vinkelrett, Coseno 90º = 0.

Den vinkelen kan også beregnes å vite at:

Scalar -produktet har følgende egenskaper:

• Commutative Property: The Order of the Vectors endrer ikke skalaren.
• Distributive eiendommer: Hvis en skalar multipliseres med summen av to vektorer, er den lik multiplikasjonen av skalar for hver vektor.

Vektorprodukt

Vektormultiplikasjonen, eller kryssprodukt av to vektorer A og B, vil resultere i en ny vektor C og uttrykker ved bruk av et kryss blant vektorene:

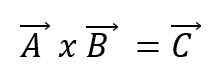
Den nye vektoren vil ha sine egne egenskaper. Den veien:

• De adresse: Denne nye vektoren vil være vinkelrett på planet, som bestemmes av de opprinnelige vektorene.
• Han føle: Dette bestemmes med høyre regel, der vektoren A blir vendt til B som peker ut retningen på rotasjonen med fingrene, og med tommelen er retningen på vektoren merket.
• Han modul: Det bestemmes ved multiplikasjon av modulene til AXB -vektorene, av barnet i den mindre vinkelen som eksisterer mellom disse vektorene. Det kommer til uttrykk:

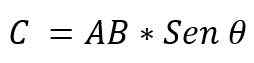
Verdien av vinkelen som eksisterer mellom de to vektorene vil avhenge av om disse er parallelle eller vinkelrett. Så det er mulig å bekrefte følgende:

• Hvis vektorene er parallelle og har samme betydning, sinus 0º = 0.
• Hvis vektorene er parallelle og har motsatte sanser, sinus 180º = 0.
• Hvis vektorene er vinkelrett, sinus 90º = 1.

Når et vektorprodukt uttrykkes i henhold til basevektorene, må det:

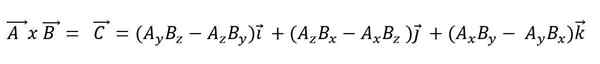
Scalar -produktet har følgende egenskaper:

• Det er ikke kommutativt: Vektorens rekkefølge endrer skalaren.
• Distributive eiendommer: Hvis en skalar multipliseres med summen av to vektorer, er den lik multiplikasjonen av skalar for hver vektor.