Perpendikulære linjekarakteristikker, eksempler, øvelser

EN vinkelrett linje Det er en som danner en vinkel på 90º med hensyn til en annen linje, kurve eller overflate. Legg merke til at når to linjer er vinkelrett og på samme plan, når de er kuttet, danner de fire identiske vinkler, hver av 90º.

Hvis et av vinklene ikke er 90º, sies det at linjene er skrå. Vinkelrett linjer er hyppige i design, arkitektur og konstruksjon, for eksempel rørnettverket til følgende bilde.

Figur 1. Rett -vinkelrør og mange vinkelrett linjer. Hvor mange 90º vinkler kan telles i dette bildet? Kilde: Piqssels.

Orienteringen av de vinkelrette linjene kan være mangfoldig, for eksempel de som er vist nedenfor:

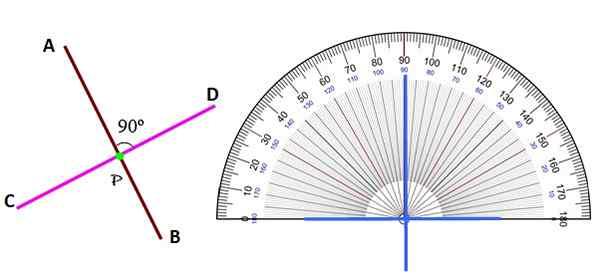
Figur 2. Vinkelrett linjer på flyet. Kilde: f. Zapata.

Uansett posisjon blir de vinkelrett linjene gjenkjent ved å identifisere vinkelen mellom dem som 90º, ved hjelp av transportøren.

Merk at i motsetning til de parallelle linjene i planet, som aldri er krysset, gjør vinkelrett alltid det på et punkt P, kalt fot av en av linjene på den andre. Derfor er det også to vinkelrett linjer Secantes.

Enhver linje har uendelig vinkelrett på den, siden vi bare fortrenger AB -segmentet til venstre eller høyre på CD -segmentet, vil vi ha nye vinkelrett med en annen fot.

Imidlertid kalles den vinkelrett som passerer bare gjennom midtpunktet til et segment bisektor av nevnte segment.

[TOC]

Eksempler på vinkelrett linjer

Vinkelrett linjer er hyppige i det urbane landskapet. I det følgende bildet (figur 3) bare noen få av de mange vinkelrett linjene som blir verdsatt på den enkle fasaden til denne bygningen og dens elementer som dører, kanaler, trinn og mer: mer:

Kan tjene deg: Fourier Diskret transformert: egenskaper, applikasjoner, eksempler Figur 3. Det er mange vinkelrett linjer på fasaden til en felles bygning som denne. Kilde: Richard Kang gjennom Flickr.

Det gode er at tre linjer vinkelrett på hverandre hjelper oss å etablere plasseringen av punktene og gjenstandene i verdensrommet. Er koordinataksene identifisert som X akse, Axis y og Z Axis, Tydelig synlig i hjørnet av et rektangulært rom som følgende:

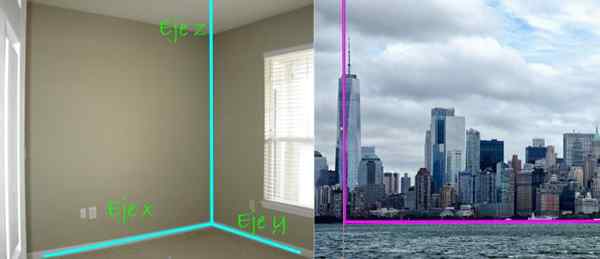Figur 4. Det kartesiske aksesystemet består av tre linjer vinkelrett på hverandre, hver har en foretrukket retning i rommet. Venstre bildekreditter: Treybunn 2 gjennom Flickr. Riktig bilde; Needpix.

I den panoramautsikten over byen, til høyre, blir også vinkelrett mellom skyskrapere og bakken advart. Den første vil si at den finnes i hele Z Axis, Mens bakken er et fly, som i dette tilfellet er flyet Xy.

Hvis bakken utgjør flyet Xy, Skyskraperen er også vinkelrett på enhver mulighet eller gate, som garanterer dens stabilitet, siden en skråstruktur er ustabil.

Og i gatene, uansett hvor rektangulære hjørner, er det vinkelrett linjer. Mange veier og gater har en vinkelrett utforming, forutsatt at land- og geografiske ulykker tillater det.

For brått å uttrykke vinkelrett mellom linjer, segmenter eller vektorer, brukes symbolet ⊥. For eksempel, hvis linjen l₁ er vinkelrett på linjen l₂, vi skrev:

L₁ ⊥ l₂

Flere eksempler på vinkelrett linjer

- I utformingen er de vinkelrette linjene veldig til stede, siden mange vanlige gjenstander er basert på firkanter og rektangler. Disse firkantede er preget av å ha 90 º indre vinkler, fordi sidene er to til to parallelle:

Det kan tjene deg: Generell parabola -ligning (eksempler og øvelser)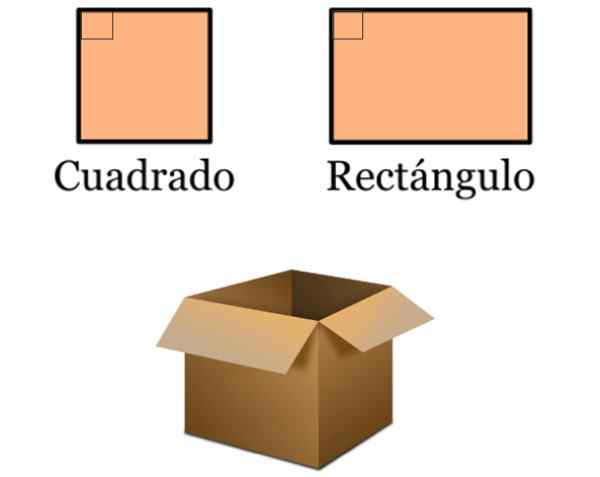 Figur 5. Torg og rektangler er en del av mange design, for eksempel denne enkle pappesten for å lagre varer. Kilde: f. Zapata.

- Domstolene som forskjellige idretter praktiseres, blir avgrenset av en rekke firkanter og rektangler. Disse inneholder igjen vinkelrett linjer.

- To av segmentene som utgjør en rektangel -trekant er vinkelrett på hverandre. Disse kalles kategorier, Mens den gjenværende linjen kalles hypotenuse.

- De elektriske feltvektorlinjene er vinkelrett på overflaten til en elektrostatisk likevekt.

- For en lastet driver, er utstyr og utstyr alltid vinkelrett på elektrisk felt.

- I rørsystemer eller kanaler som brukes til å transportere forskjellige typer væsker, for eksempel gass som vises i figur 1, er det vanlig at albuene i rette vinkler. Derfor danner de vinkelrett linjer, slik er tilfellet med et kjelerom:

Figur 6. Rør i et kjelerom. Kilde: Wikimedia Commons. Roger McLassus/CC BY-S (http: // CreativeCommons.Org/lisenser/by-SA/3.0/)

Øvelser

- Oppgave 1

Tegn to vinkelrett linjer etter regel og kompass.

Løsning

Det er veldig enkelt å gjøre, etter disse trinnene:

-Den første linjen er tegnet, kalt AB (svart).

-Over (eller under hvis foretrukket) av AB Marks Point P, der vinkelrett vil passere. Hvis P er rett over (eller under) halvparten av AB, sa vinkelrett er bisektoren til AB -segmentet.

-Med kompasset sentrert på P, tegnes en sirkel som kutter AB i to punkter, kalt til 'og B' (rød).

Kan tjene deg: vennlige eller vennlige tall: eksempler og hvordan du finner dem

-Kompasset i A'P åpnes, det fokuserer på en 'og en sirkel trekkes som passerer gjennom P (grønn).

-Gjenta forrige trinn, men åpner nå kompasset lengden på B'P -segmentet (grønn). Begge omkretsbuer er kuttet på punkt Q under P og selvfølgelig i sistnevnte.

-Punktene P og Q er sammen med regelen og den vinkelrett linjen (blå) er allerede klar.

-Endelig må alle hjelpekonstruksjoner slettes nøye, og etterlater bare vinkelrett.

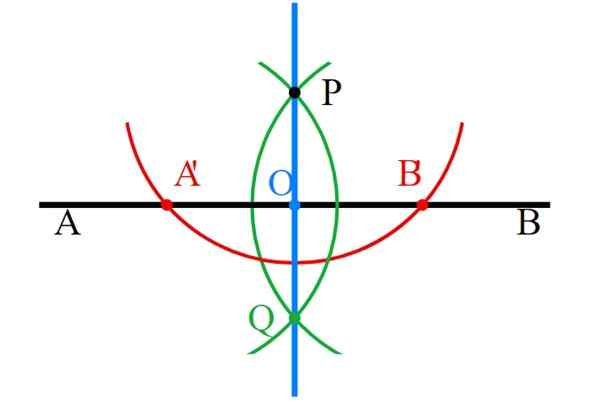Figur 6. Percendular linjer med regel og kompas. Kilde: Wikimedia Commons.

- Oppgave 2

To linjer l₁ og jeg₂ De er vinkelrett hvis deres respektive bakker m₁ og M₂ De oppfyller dette forholdet:

m₁ = -1/m₂

Gitt linjen y = 5x - 2, finn en linje vinkelrett på den og pass gjennom punktet (-1, 3).

Løsning

-Først av alt er skråningen på den vinkelrette linjen m_⊥, Som antydet i uttalelsen. Hellingen på den opprinnelige linjen er M = 5, koeffisienten som følger med "X". Så:

m_⊥= -1/5

-Da bygges ligningen for den vinkelrett linjen og_⊥, erstatte den tidligere funnet verdien:

og_⊥= -1/5x + b

-Deretter bestemmes verdien av B ved hjelp av poenget gitt av uttalelsen, (-1,3), siden den vinkelrette linjen må passere gjennom den:

y = 3

x = -1

Erstatte:

3 = -1/5 (-1) + b

Verdien av B er fjernet:

B = 3- (1/5) = 14/5

-Endelig er den endelige ligningen bygget:

og_⊥= -1/5x + 14/5

Referanser

1. Baldor, a. 2004. Flat og romgeometri. Kulturpublikasjoner.
2. Clemens, s. 2001. Geometri med applikasjoner og problemløsning. Addison Wesley.
3. Matematikk er morsomt. Vinkelrett linjer. Gjenopprettet fra: Mathisfun.com.
4. Monterey Institute. Vinkelrett linjer. Gjenopprettet fra: MontereyInstitute.org.
5. Wikipedia. Vinkelrett linjer. Gjenopprettet fra: er.Wikipedia.org.