Vertikal linje

Vi forklarer hva en vertikal, dens egenskaper og applikasjoner i matematikk.

Et eksempel på vertikal linje

Hva er en vertikal linje?

EN vertikal linje Det er den som følger retningen som ethvert objekt faller til bakken når den frigjøres fra en viss høyde og er vinkelrett på horisontlinjen, siden den dannes med denne en vinkel på 90º. 

Når du tegner det, er et slag laget av topp til bunn eller omvendt. Sidekantene på skjermen til en dataskjerm er eksempler på vertikale linjer, så vel som den rette bagasjerommet på mange trær.

I arkitektur og design antyder den vertikale linjen hos mennesker en følelse av dynamikk, bevegelse, kraft og høyde, i motsetning til horisontale linjer, som antyder hvile og avslapning. Når noen er oppreist, det vil si at deres posisjon er vertikal og vinkelrett med hensyn til bakken, er den klar til å gå, løpe og generelt gå inn i bevegelse.

Du kan finne mange vertikale linjer i kunst, fotografier og menneskelige konstruksjoner, permanente eller passasjerer, for eksempel de som er dannet ved kontraster mellom lys og skygge på veggene, gjennom dagen.

Den vertikale linjen brukes også til å beskrive en veldig vanlig bevegelse i naturen: fritt fall, samt beskrive retningen til andre krefter, bortsett fra den nevnte tyngdekraften, når de virker vinkelrett på en viss overflate.

Matematisk form av den vertikale linjen

I matematikk og geometri sammenfaller den vertikale linjen med den "y" kartesiske aksen, aksen til den avhengige variabelen, mens den horisontale aksen tilsvarer "x" -aksen, den for den uavhengige variabelen.

En vertikal linje kan enkelt tegne på det kartesiske planet, da det tilsvarer ligningen:

Kan tjene deg: statistiske variabler

x = k

Hvor k er en konstant. De vertikale linjene er alltid parallelle med Y -aksen, for eksempel linjen X = −3 som vises i rødt i følgende figur:

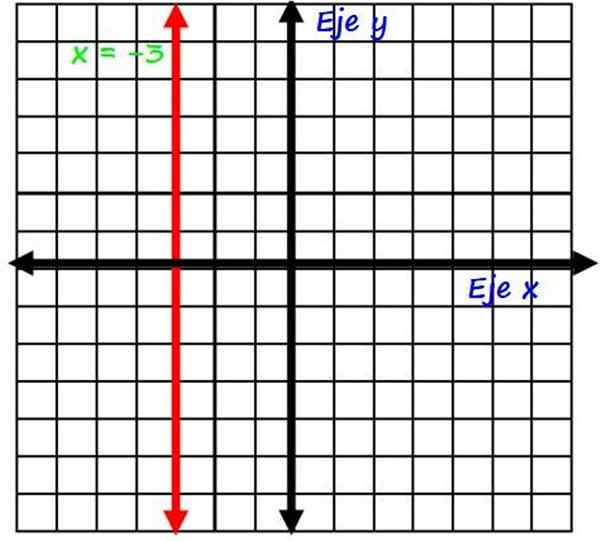Graf over den vertikale linjen x = −3. Kilde: f. Zapata.

Merk at alle punktene på denne linjen alltid har samme x -koordinat, for eksempel punktene (−3, 0); (−3, 1), (−3, 2) og mer. I tillegg er den rette røde linjen til den horisontale aksen i x = −3 koordinat.

På den annen side er ligningslinjen x = 0 en annen måte å uttrykke den vertikale aksen eller aksen.

I påvente av vertikal linje

Det anses at en vertikal linje mangler definert skråning, eller det kan også sies at den vertikale linjen har en uendelig skråning, mens skråningen til en horisontal linje er 0.

Når det gjelder å bruke formelen for å beregne skråningen på en linje: M = Δy/ Δx når du beregner helningen på den vertikale linjen, hender det at Δx alltid er lik 0, siden et hvilket som helst punkt som er valgt har samme koordinat x x. Husk at Δx = x₂ - x₁, det vil si forskjellen mellom x -koordinatene til to vilkårlige punkter.

Så prøver å erstatte Δx = 0 i skråningsligningen, er det funnet at:

M = Δy/ 0

Og siden divisjonen med 0 ikke er en definert operasjon, viser det seg at skråningen til en hvilken som helst vertikal linje er ubestemt, uavhengig av verdien av Δy.

Vertikal linjetest 

I motsetning til den horisontale linjen, som er grafen til den konstante funksjonen, er den vertikale linjen x = k ikke en funksjon, siden den samme verdien av form uendelig par bestilt med verdiene til y, som strider mot definisjonen av funksjon ( I dette har en X -verdi ett og bare ett bilde i Y).

Kan tjene deg: aksial symmetri: egenskaper, eksempler og øvelser

Imidlertid kan den vertikale linjen brukes til å bestemme visuelt om en kurve utgjør en funksjon eller ikke. Kriteriet er veldig enkelt: en vertikal er tegnet som kutter kurven det gjelder. Hvis du gjør det på mer enn ett punkt, er det ikke en funksjon.

Tenk for eksempel på kurven som er vist nedenfor, som du vil vite om den tilsvarer grafen til noen funksjon.

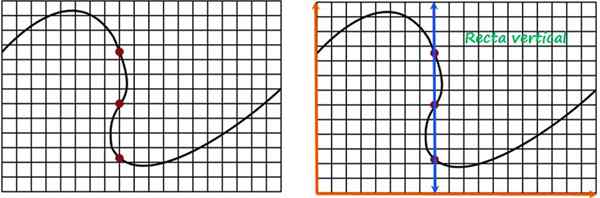Vertikal linjetest for å vite om en kurve tilsvarer grafen til en funksjon. Kilde: f. Zapata.

Den samme vertikale linjen passerer gjennom de røde punktene, og siden den kutter kurven til mer enn ett punkt, konkluderes det med at det ikke er grafen til en funksjon.

Vertikale asymptoter

De er vertikale linjer som grafen til en funksjon ikke kan krysse. De oppstår fordi når den nærmer seg en viss verdi av x, vokser funksjonen eller avtar på ubestemt tid. Selvfølgelig hører ikke denne x -verdien til funksjonen til funksjonen.

Når det gjelder en rasjonell funksjon, er verdiene til X som har sin vertikale asymptoter de som avbryter nevneren. I dette tilfellet, når du prøver å erstatte den verdien av x, ville det være en inndeling mellom 0, som ikke er mulig å utføre, som forklart ovenfor.

Det som er mulig å gjøre er å dele et begrenset beløp med et annet beløp så lite du vil, forutsatt at beløpet ikke er akkurat 0.

I slike tilfeller kan resultatet av divisjonen være et ekstremt stort antall (eller lite fordi den er negativt, avhenger av tegnet på telleren). Leseren kan sjekke dette ved å dele for eksempel:

Kan tjene deg: vektorbeløp

2 ÷ 0.000001 = 2 000 000

Anta at verdien av x som annulterer nevneren til den rasjonelle funksjonen er x = b. Når en verdi veldig nær B (men ikke akkurat B) erstattes i funksjonen, har en inndeling mellom en endelig og en ekstremt liten mengde oppstår.

Det er grunnen til.

Eksempel på vertikal asymptote

Ovennevnte er bekreftet med den rasjonelle funksjonen:

Verdien som avbryter nevneren er x = 2, derfor har funksjonen en vertikal asymptot på linjen x = 2. Anta at du vil nærme deg x = 2 ta en knapt mindre verdi, for eksempel x = 1.9999:

Dette var en tilnærming til x = 2 fra venstre, og resultatet er at funksjonen blir veldig negativ, det vil si at den har en tendens til negativ uendelig. Nå kan du prøve en tilnærming til høyre, for eksempel x = 2.0001:

Og det ser at funksjonen beveger seg bort mot positiv uendelig. Grafen bekrefter det:

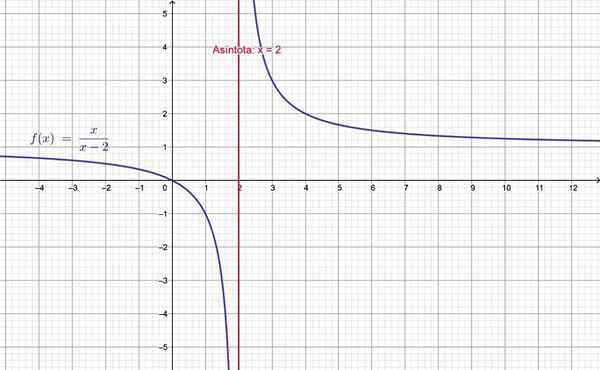Den vertikale linjen x = 2 er asymptote av F (x). Kilde: f. Zapata.

Referanser

1. Atlantic Union Conference Teacher Bulletin. Horisontale og vertikale linjer. Gjenopprettet fra: TeacherBulintin.org.
2. Byju's. Vertikal linje. Gjenopprettet fra: Byjus.com.
3. CK-12. Grafisk av horisontale og vertikale linjer. Hentet fra: CK-12.org.
4. Stewart, J. 2006. Forkalkning: Matematikk for beregning. 5. plass. Utgave. Cengage Learning.
5. Zill, d. 1984. Algebra og trigonometri. 1. Utgave. McGraw Hill.