Matte

Negativ homotecia

Negativ homotecia
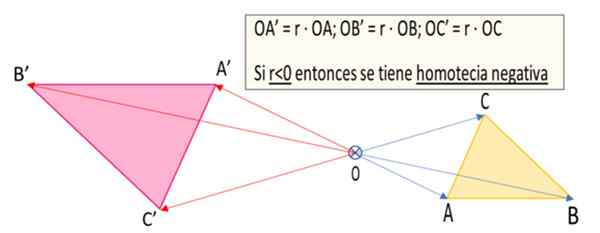
Figur 1. Triangle A'B'c 'er den homotetiske transformasjonen av ABC -trekanten med hensyn til punktet eller med en grunn til negativ homotecia r = -1.5 (Utarbeidet av: F Zapata).

Hva er negativ homotecia?

Negativ homotecia er en transformasjon der en polygon inneholdt i et plan har som sitt bilde en annen polygon i det samme planet, av like vinkler og med de tilsvarende sidene proporsjonalt med de av originalen. Når homotecia er negativt, roteres bildet en halv sving med hensyn til det første figuret.

Homotecia er preget av å ha et homotecia -senter ENTEN og en proporsjonalitetskonstant kalt fornuft r. Når r Det er et negativt tall, så det er snakk om negativ homotecia.

Hvordan gjøres en homotecia -transformasjon?

For å forklare hvordan en negativ homotecia utføres, vil vi ta tilfellet med figur 1 der en trekant er ABC som vil bygge sin negative homotetiske.

1.- Det begynner å velge et homotecia -senter, som er denne saken er poenget ENTEN.

2.- Fra ENTEN Orienterte segmenter er bygget (vektorer) Oa, Ob og OC som går fra sentrum av homotecia til hver av toppunktene i trekanten.

3.- En homotecia -grunn er valgt r. Som du vil ha en negativ homotecia, så r Det må være mindre enn null. I tilfelle av figur 1 ble det tatt R = -1.5.

4.- Vektorer er tegnet Oa ', Ob ' og Oc ', som er henholdsvis Oa '= r ∙ oa, Ob '= r ∙ ob  og Oc '= r ∙ Oc. Som R = -1.5, det er et negativt tall, så vektorene Oa ', Ob ' og Oc ' De har retning i strid med deres tilsvarende kolleger, det vil si Oa, Ob og OC. Men som den absolutte verdien av fornuft r er | R | = 1.5 størrelsene på Oa ', Ob'Og Oc ' De er en annen halvparten større enn sine kolleger Oa, Ob og OC.

5.- Tipsene til vektorene Oa ', Ob ' og Oc ' definere toppunktene til trekanten A'b'c ' Hva er den negative homotetiske av trekanten ABC.

Egenskaper for negativ homotecia

De negativ homotecia, også kalt Inverse Homotecia, Den har følgende egenskaper:

Det kan tjene deg: Multipler av 8: Hva er og forklaring

1.- De tilsvarende sidene mellom bildet polygon og den opprinnelige polygon har proporsjonale lengder, og er konstant av proporsjonalitet den absolutte verdien av homotecia -forholdet, det vil si at bildet er forsterket i en faktor | r | så lenge som | r | er større enn enheten, men bildet reduseres hvis | r | er mindre enn enheten.

2.- Vinklene mellom de tilsvarende sidene av bildet og den opprinnelige figuren har de samme tiltakene.

3.- De homologe sidene mellom original og bilde er parallelle med hverandre.

4.- De tilsvarende segmentene når det gjelder negativ homotecia er parallelle, men med veiledning eller motsatt retning. For eksempel i figur 1 har segment AB sin homologe A'B 'parallell med den første, men med motsatt retning.

Sammenligning med positiv homotecia

Det kalles positivt homotecia at homotecia -forholdet er et positivt tall. For å bygge et positivt homotecia følges de samme trinnene som for negativ homotecia:

1.- Velg et homotecia -senter, i vårt tilfelle poenget ENTEN (Se figur 2).

2.- Tegn de orienterte segmentene (vektorene), alt fra sentrum av homotecia til toppunktene til polygon, i tilfelle av figur 2 er disse: Oa, Ob og OC.

3.- Velg et homotecia -forhold som er et positivt tall, for eksempel i tilfelle av figur 2 er det valgt R = 0.5.

4.- Vektorer er tegnet Oa ', Ob ' og Oc ', som er henholdsvis Oa '= r ∙ oa, Ob '= r ∙ ob og Oc '= r ∙ Oc. Som r Det er et positivt tall, så vektorene Oa ', Ob ' og Oc ' De har samme adresse som Oa, Ob og OC. Lengden på Oa ', Ob'Og Oc ' De er halvparten av at deres kolleger Oa, Ob og OC, Siden grunnen er R = 0.5.

5.- Endelig blir A'B'c 'toppunktene sammen med for å oppnå den homotetiske trekanten til ABC med fornuft 1/2.

Kan tjene deg: firkantet: elementer, egenskaper, klassifisering, eksempler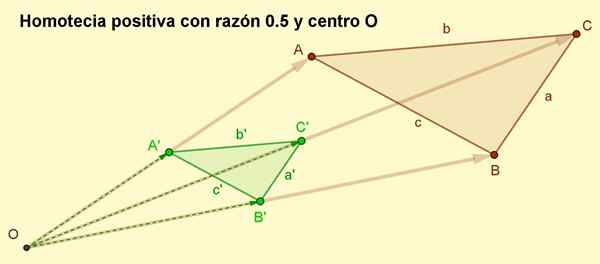 Figur 2. Positiv homotecia med rette 0,5 av ABC -trekantresultatene. I positivt homotecia opprettholdes orienteringen. (Utarbeidet av: f. Zapata)

Homotecia eksempler

Homotecia vises i forskjellige situasjoner:

Filmprojektorer

I en filmprojektor blir bildet registrert i en ramme projisert og utvides på en skjerm, og for at projeksjonen skal sees til høyre, er det nødvendig at rammen er investert, siden Homotecia Center er i midten av linsen til den Linsen til linsen til projektoren, mellom rammen og skjermen (negativ homotecia, se figur 3)

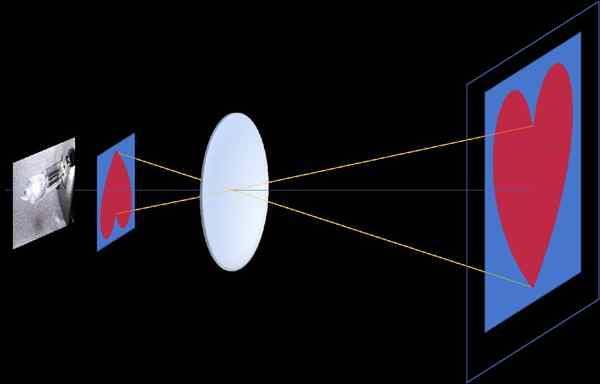Figur 3. Negativ homotecia vises i filmprojektoren, mellom bildet registrert på en gjennomskinnelig ramme og bildet projisert på skjermen. Homotecia -senteret er på det optiske sentrum av linsen, på sin side som ligger mellom rammen og skjermen. Kilde: f. Zapata.

Fotokameraer

Dette prinsippet gjelder også for kameraene: lyset fra bildet som ligger en vis.

Bildet registrert i sensoren er omvendt med hensyn til den virkelige og er vanligvis proporsjonalt mindre enn henne.

Praktisk anvendelse

Solen skal ikke se direkte, fordi den forårsaker permanent skade på netthinnen, men det er to muligheter for å studere den: bruk filtre som demper lysintensiteten eller projiserer bildet på en skjerm.

Kan tjene deg: proporsjonal variasjon

En projeksjonsenhet består av et lengderør d. En av endene av røret er dekket med aluminiumsfolie og øvelser i sentrum med en pin. Den andre enden, som vil tjene som en skjerm, er dekket med gjennomskinnelig papir, som kan være løkpapir eller albanenpapir (grønnsakspapir).

Trening

Bestem solens diameter, vel vitende om at den terrestriske orbitalradiusen er i størrelsesorden 150 millioner kilometer, at projeksjonsrøret, for eksempel det vist i figur 4, er 2,2 meter i lengde og at det projiserte bildet er 2, 1 cm i diameter.

Figur 4. I røret for å projisere solskiven oppstår et negativt homotecia -forhold. Kilde: f. Zapata.

Løsning

Dataene er som følger:

  • Rørlengde: D = 2,2m
  • Solens projiserte bildediameter: S = 2,1 cm
  • Avstand fra solrøret: r = 150 x 10^9 m
  • Ekte soldiameter: S = ¿?

For å oppnå solens diameter påføres et proporsjonalitetsforhold i henhold til proporsjonaliteten av homotecia (se figur 4):

Avstanden til solen er i lengden på røret da solens diameter er til diameteren til det projiserte bildet:

(R / d) = (s / s)

Å rydde denne likheten om at solens virkelige diameter har diameteren på projeksjonen multiplisert med kvotienten mellom avstanden til solen og rørets lengde:

S = S (R / D)

Å plassere de numeriske verdiene er:

S = 2,1 x 10-2 M (150 x 109 m / 2,2 m)

S = 1,43 x 109 m.

Dette resultatet tolkes som følger: solens virkelige diameter er 1,43 millioner kilometer.

Referanser

  1. Álvaro Rendón, til. R. 2004. Teknisk tegning: Aktivitetsnotatbok.
  2. Antonio Álvarez de la Rosa, J. L. 2002. Affinitet, homologi og homotecia.
  3. Baer, ​​r. 2012. Lineær algebra og projektiv geometri. Couer Corporation.
  4. Hebert, og. 1980. Generell matematikk, sannsynligheter og statistikk.
  5. Messerve, f. OG. 2014. Grunnleggende begreper av geometri. Couer Corporation