Vektorstørrelse

Hva er en vektorstørrelse?

EN Vektorstørrelse Det er et hvilket som helst uttrykk representert av en vektor som har numerisk verdi (modul), retning, retning og applikasjonssted. Noen eksempler på vektorstørrelser er forskyvning, hastighet, styrke og elektrisk felt.

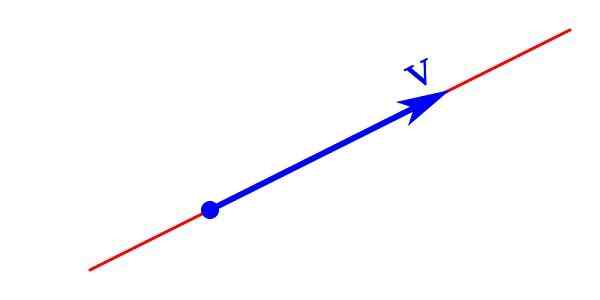
Den grafiske representasjonen av en vektorstørrelse består av en pil hvis spiss indikerer dens retning og retning, lengden er modulen og utgangspunktet er opprinnelsespunktet eller poenget.

Grafisk representasjon av en vektor

Vektorstørrelsen er representert analytisk med en bokstav som bærer en pil på toppen peker til høyre i horisontal retning. Det kan også være representert med et brev skrevet med fet skrift V hvis modul ǀVǀ Det er skrevet i kursiv V.

En av anvendelsene av konseptet med vektorstørrelse er i utformingen av motorveier og veier, spesielt i utformingen av dets krumning. En annen applikasjon er beregning av forskyvning mellom to steder eller hastighetsendringen av et kjøretøy.

Elementer i en vektorstørrelse

En vektorstørrelse er en hvilken som helst enhet representert av et linjesegment, med orientering i rommet, som har egenskapene til en vektor. Elementene er:

Modul: Det er den numeriske verdien som indikerer størrelsen eller intensiteten til vektorstørrelsen.

Adresse: Det er orienteringen til linjesegmentet i det rommet som inneholder det. Vektoren kan ha horisontal, vertikal eller skrå retning; Nord, sør, dette eller vest; Nordøst, sørøst, sørvest eller nordvest.

Føle: Det er indikert med spissen av pilen i enden av vektoren.

Det kan tjene deg: Fysikk før grekerne (Antigua Hellas)

Søknadspunkt: Det er opprinnelsen eller punktet for innledende virkning av vektoren.

Vektorklassifisering

Vektorer er klassifisert som kollinære, parallelle, vinkelrett, samtidig, koblinger, gratis, glidende, motsatt, utstyr, fast og enhet.

Colineal: De hører hjemme eller handler på den samme rette linjen, de kalles også Lineært avhengig Og de kan være vertikale, horisontale og tilbøyelige.

Paralleller: De har samme adresse eller tilbøyelighet.

Vinkelrett: To vektorer er vinkelrett på hverandre når vinkelen mellom dem er 90 °.

Samtidig: De er vektorer som når de glir over sin handlingslinje sammenfaller de på samme punkt i verdensrommet.

Coplanarios: De handler i et fly, for eksempel flyet Xy.

Gratis: De beveger seg hvor som helst i rommet og holder modulen, retningen og betydningen.

Lysbilde: De beveger seg langs handlingslinjen bestemt av deres retning.

Motsetninger: De har samme modul og retning, og motsatt retning.

Utstyr: De har samme modul, retning og mening.

Fikset: Søknadspunktet har ufravikelig.

Enheter: Vektorer hvis modul er enheten.

Vektorkomponenter

En vektorstørrelse i et tredimensjonalt rom er representert i et system med tre akser vinkelrett på hverandre (X og z) kalt ortogonal prøvd.

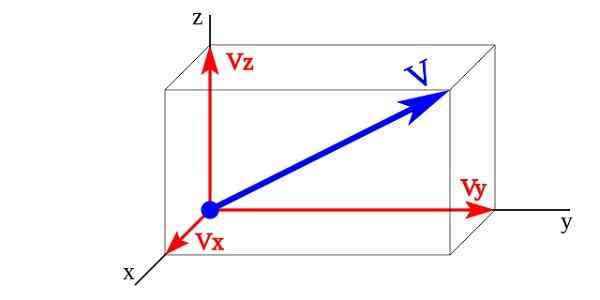Vektorkomponenter i en vektorstørrelse

På bildet vektorene Vx, Vy, Vz er vektorvektorkomponentene V hvis enhetsvektorer er x,og,z. Vektorstørrelsen V Det er representert av summen av vektorkomponentene.

V = Vx + Vy + Vz

Resultatet av flere vektorstørrelser er vektorsummen til alle vektorer og erstatter disse vektorene i et system.

Vektorfelt

Vektorfeltet er regionen av rom der i hvert av punktene en vektorstørrelse tilsvarer. Hvis størrelsen som manifesteres er en kraft som virker på et kropp eller et fysisk system, er vektorfeltet et felt av krefter.

Kan tjene deg: Steiner Theorem: Forklaring, applikasjoner, øvelser

Vektorfeltet er representert grafisk av feltlinjer som er tangente linjer i vektorstørrelsen på alle punkter i regionen. Noen eksempler på vektorfelt er det elektriske feltet som er opprettet av en punktlig elektrisk ladning i rom- og hastighetsfeltet til en væske.

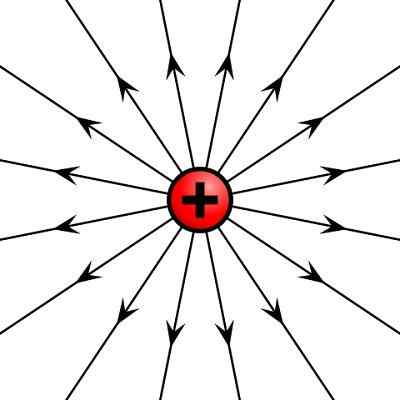Elektrisk felt opprettet av en positiv elektrisk lading

Operasjoner med vektorer

Tillegg av vektorer: Det er resultatet av to eller flere vektorer. Hvis du har to vektorer ENTEN og P Summen er ENTEN + P = q. Vektoren Q Det er den resulterende vektoren som oppnås grafisk å flytte opprinnelsen til vektoren TIL til slutten av vektoren B.

Vektor subtraksjon: Subtraksjon av to vektorer eller og P er ENTEN - P = Q. Vektoren Q  Du får tilsetning av vektoren ENTEN Ditt motsatte -P. Den grafiske metoden er den samme som summen med forskjellen at den motsatte vektoren overføres til det ekstreme.

Skalarprodukt: Produktet av en skalær størrelse til med en vektorstørrelse P Det er en vektor MP som har samme retning av vektoren P. Hvis skalarstørrelsen er null, er skalarproduktet en nullvektor.

Eksempler på vektorstørrelser

Posisjon

Plasseringen av et objekt eller partikkel med hensyn til et referansesystem er en vektor som er gitt av dets rektangulære koordinater X og z, og er representert av vektorkomponentene Xî, Yĵ, Zk. Vektorene  Yo, ĵ, k De er enhetsvektorer.

En partikkel på et tidspunkt (X og z) har en posisjonsvektor r = Xî + Yĵ + Zk. Den numeriske verdien av vektorposisjonen er r= √ (x² + og² + z²). Endringen i partikkelposisjon fra en posisjon til en annen med hensyn til et referansesystem er vektoren Forskyvning ΔR Og det beregnes med følgende vektoruttrykk:

Kan tjene deg: anodiske stråler

Δr = r₂ - r₁

Akselerasjon

Gjennomsnittlig akselerasjon (til_m) Det er definert som variasjonen av hastigheten v I et tidsintervall Δt Og uttrykket for å beregne det er til_m= ΔV/Δt, å være ΔV Vektorendringshastigheten.

Øyeblikkelig akselerasjon (til) er grensen for gjennomsnittlig akselerasjon til_m når Δt blir så liten at det har en tendens til null. Øyeblikkelig akselerasjon uttrykkes i henhold til vektorkomponentene

til =til_xYo +til_og ĵ+ til_zk

Gravitasjonsfelt

Gravitasjonsattraksjonskraften utøvd av en masse M, Ligger ved opprinnelsen, på en annen masse m På et tidspunkt i verdensrommet x, og, z Det er et vektorfelt som kalles gravitasjonskraftfelt. Denne kraften er gitt av uttrykket:

F= (-mmg/r)ȓ

r = Xî + Yĵ + Zk

F = Det er gravitasjonskraft for fysisk størrelse

G = er den universelle gravitasjonen konstant

ȓ = er masseposisjonsvektoren m

Referanser

1. Tallack, J C. Introduksjon til vektoranalyse. Cambridge: Cambridge University Press, 2009.
2. Spiegel, M R, Lipschutz, S og Spellman, D. Analysevektor. s.l. : Mc Graw Hill, 2009.
3. Merkevare, l. Analysevektor. New York: Dover Publications, 2006.
4. Griffiths, D J. Introduksjon til elektodynamikk. New Jersey: Prentice Hall, 1999. p. 1-10.
5. Haag, f. En introduksjon til vektoranalyse. Glasgow: Methuen & Co. Ltd, 2012.