Diskret matematikk

Hva er diskret matematikk?

De Diskret matematikk samsvarer med et område av matematikk som er ansvarlig for å studere settet med naturlige tall; det vil si settet med endelige og uendelige regnskapsnumre der elementene kan telles separat, en etter en.

Disse settene er kjent som diskrete sett; Et eksempel på disse settene er hele tall, grafer eller logiske uttrykk, og brukes innen forskjellige vitenskapsfelt, hovedsakelig innen informatikk eller databehandling.

Beskrivelse

I diskret matematikk er prosessene tallrike, de er basert på hele tallene. Dette betyr at desimaltall ikke brukes, og derfor brukes ikke tilnærmingen eller grensene, som på andre områder, heller ikke. For eksempel kan en ukjent være lik 5 eller 6, men aldri 4,99 eller 5.9.

På den annen side, i den grafiske representasjonen, vil variablene være diskrete og er gitt fra et begrenset sett med punkter, som telles en etter en, som observert i bildet:

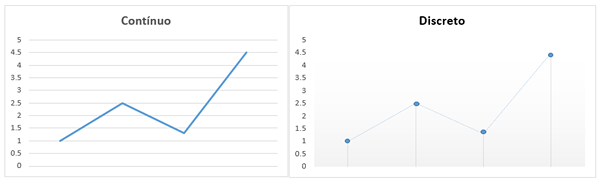
Diskret matematikk blir født på grunn av behovet for å få en nøyaktig studie som kan kombineres og beviste, for å bruke den på forskjellige områder.

Hva er diskret matematikk for?

Diskret matematikk brukes i flere områder. Blant de viktigste er følgende:

Kombinatorisk

Studere endelige sett der elementene kan bestilles eller kombineres og tilbakekalles.

Diskret distribusjonsteori

Studiehendelser som oppstår i rom der prøver kan regnskapsføres, der kontinuerlig fordeling brukes til å nærme seg diskrete distribusjoner, eller motsatt.

Informasjonsteori

Det refererer til koding av informasjon, brukt til design og overføring og lagring av data, for eksempel lignende signaler.

Kan tjene deg: Trachtenberg -metode: Hva er det, eksempler

Databehandling

Gjennom diskret matematikk løses problemer ved bruk av algoritmer, samt hva som kan beregnes og tiden det tar å gjøre det (kompleksitet).

Betydningen av diskret matematikk i dette området har økt de siste tiårene, spesielt for utvikling av programmering og Programvare.

Kryptografi

Det er basert på diskret matematikk for å lage sikkerhetsstrukturer eller krypteringsmetoder. Et eksempel på denne applikasjonen er passord, og sender separate biter som inneholder informasjon.

Gjennom studien kan egenskapene til hele tall og primtall (teori om tall) opprettes eller ødelegges.

Logikk

Diskrete strukturer brukes, som vanligvis danner et begrenset sett, for å demonstrere teoremer eller for eksempel bekrefte programvare.

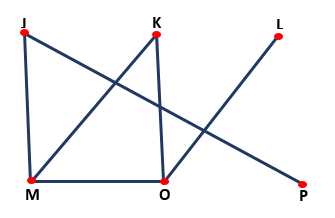
Grafteori

Det tillater oppløsning av logiske problemer ved å bruke noder og linjer som danner en type graf, som vist i følgende bilde:

Algebra

Det er et område som er nært knyttet til diskret matematikk fordi algebraiske uttrykk er diskret. Gjennom disse elektroniske kretsløpene er prosessorer, programmering (boolsk algebra) og databaser (relasjonell algebra) utviklet (relasjonell algebra).

Geometri

Studer de kombinatoriske egenskapene til geometriske objekter, for eksempel planbelegg. På den annen side gjør beregningsgeometri det mulig å utvikle geometriske problemer ved å bruke algoritmer.

Sett teori

I diskret matematikk er settene (endelig og uendelig numbable) det viktigste objektive målet. Set -teorien ble publisert av George Cantor, som viste at alle uendelige sett er i samme størrelse.

Et sett er en gruppe elementer (tall, ting, dyr og mennesker, blant andre) som er godt definert; det vil si at det er et forhold som hvert element tilhører et sett, og uttrykkes for eksempel A ∈ A.

Kan tjene deg: Egenskaper for likhet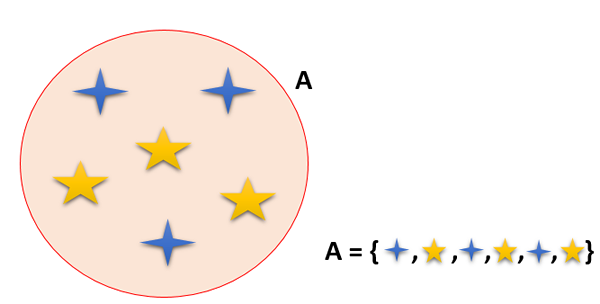

I matematikk er det forskjellige sett som grupperer visse tall i henhold til deres egenskaper. Dermed har de for eksempel:

- Sett med naturlige tall n = 0, 1, 2, 3, 4, 5, 6,… +∞.

- Sett med hele tall e = -∞…, -3, -2, -1, 0, 1, 2, 3,… +∞.

- Undergruppe av rasjonelle tall q* = -∞…, - ¼, - ½, 0, ¼, ½,… ∞.

- Sett med reelle tall r = -∞…, -½, -1, 0, ½, 1,… ∞.

Settene er navngitt med alfabetbrev, med store bokstaver; Mens elementene er navngitt i små bokstaver, innvendige nøkler () og atskilt med komma (,). De er generelt representert på diagrammer som Venn og Caroll, samt beregningsmessig.

Med grunnleggende operasjoner som union, kryss, komplement, forskjell og kartesisk produkt, styres settene og elementene deres, basert på tilhørighetsforholdet.

Det er flere typer sett, de mest studerte i diskret matematikk er følgende:

Endelig sett

Det er en som har et begrenset antall elementer og som tilsvarer et naturlig tall. Dermed er for eksempel a = 1, 2, 3,4 et begrenset sett som har 4 elementer.

Uendelig regnskapssett

Det er en der det er en korrespondanse mellom elementene i et sett og de naturlige tallene; det vil si fra et element alle elementer i et sett kan vises suksessivt.

På denne måten vil hvert element tilsvare hvert element i settet med naturlige tall. For eksempel:

Hele hele tallene z = … -2, -1, 0, 1, 2… kan vises som z = 0, 1, -1, 2, -2…. På denne måten er det mulig å lage en en -til -en -korrespondanse mellom elementene i Z og de naturlige tallene, som det kan sees i følgende bilde:

Kan tjene deg: beregning av tilnærminger ved bruk av differensialer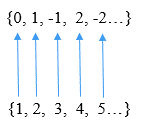

Diskretisering

Det er en metode som brukes for å løse kontinuerlige problemer (modeller og ligninger) som må konverteres til diskrete problemer, der løsningen er kjent med tilnærmingen til løsningen av det kontinuerlige problemet.

Sett en ellers prøver skjønnsmessigheten å få en begrenset mengde av et uendelig sett med punkter; På denne måten blir en kontinuerlig enhet transformert til individuelle enheter.

Generelt brukes denne metoden i den numeriske analysen, for eksempel i løsningen av en differensialligning, gjennom en funksjon som er representert med en begrenset mengde data i dets domene, selv når dette er kontinuerlig.

Et annet eksempel på diskretiseringen er bruken av det til å konvertere et analogt til digitalt signal, når kontinuerlige signalenheter blir konvertert til individuelle enheter (de blir diskret), og deretter kodet og kvantifisert for å oppnå digitalt signal.

Referanser

1. Grimaldi, r. P. (1997). Diskret og kombinatorisk matematikk. Redaksjonell Addison Wesley Iberoamericana.
2. Ferrando, v. Gregori. (nitten nitti fem). Diskret matematikk. REVERTE.
3. Jech, t. (2011). Sett teori. Stanford Encyclopedia of Philosophy.
4. José Francisco Villalpando Becerra, A. G. (2014). Diskret matematikk: applikasjoner og øvelser. Patria redaksjonell gruppe.
5. Landau, r. (2005). Databehandling, til første kurs i vitenskapelig.
6. Merayo, f. G. (2005). Diskret matematikk. Thomson redaksjon.
7. Rosen, k. H. (2003). Diskret matematikk og dens applikasjoner. McGraw-Hill-redaksjonen.
8. Schneider, d. G. (nitten nitti fem). En logisk tilnærming til diskret matematikk.