Inverse matriseberegning og trening løst
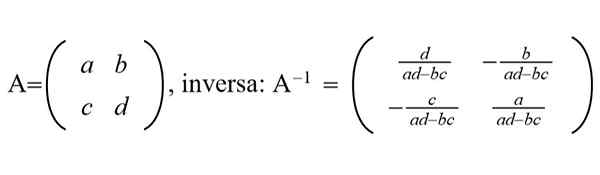
- 3878
- 479
- Jonathan Moe
De Inverse matrise Av en gitt matrise er det matrisen som multiplisert med originalen resulterer i identitetsmatrisen. Den omvendte matrisen er nyttig for å løse systemer for lineære ligninger, derav viktigheten av å vite hvordan du beregner den.
Matrisene er veldig nyttige innen fysikk, ingeniørfag og matematikk, siden de er et kompakt verktøy for å løse komplekse problemer. Nytten av matriser forbedres når de er invertible og også deres omvendte er kjent.
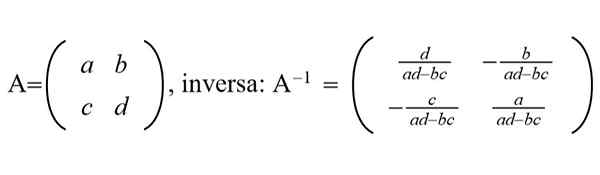 Figur 1. En generisk 2 × 2 -matrise og dens inverse matrise vises. (Utarbeidet av Ricardo Pérez)
Figur 1. En generisk 2 × 2 -matrise og dens inverse matrise vises. (Utarbeidet av Ricardo Pérez) I de grafiske prosesseringsfeltene brukes Big Data, Data Mining, Machine Learning og andre effektive og raske algoritmer for å evaluere NXN -matriser om Inverse Matrix med N veldig stor, i størrelsesorden tusenvis eller millioner.
For å illustrere bruken av omvendt matrise i styringen av systemet med lineære ligninger vil vi begynne med det enkleste tilfellet av alle: 1 × 1 matriser.
Det enkleste tilfellet: En lineær ligning av en enkelt variabel vurderes: 2 x = 10.
Tanken er å finne verdien av x, men den vil være "matrise".
Matrisen M = (2) som multipliserer vektoren (x) er en 1 × 1 matrise som resulterer i vektoren (10):
M (x) = (10)
Det inverse av M -matrisen er betegnet med m-1.
Den generelle måten å skrive dette "lineære systemet" er:
M x = b, der x er vektoren (x) og b er vektoren (10).
Per definisjon er den omvendte matrisen en som multiplisert med den opprinnelige matrisen resulterer i identitetsmatrisen I:
M-1 M = i
I saken vurdert, matrise m-1 Det er matrisen (½), det vil si m-1 = (½) siden m-1 M = (½) (2) = (1) = i
Kan tjene deg: 90 Divisors: Hva er og forklaringFor å finne den ukjente vektoren x = (x), i den hevede ligningen, multipliseres begge medlemmene med omvendt matrise:
M-1 M (x) = m-1 (10)
(½) (2) (x) = (½) (10)
(½ 2) (x) = (½ 10)
(1) (x) = (5)
(x) = (5)
Likhet på to vektorer er nådd, som er de samme når deres tilsvarende elementer er like, det vil si x = 5.
Beregning av inverse av en matrise
Det som motiverer beregningen av omvendt matrise er å finne en universell metode for løsningen av lineære systemer som følgende 2 × 2 -system:
x - 2 y = 3
-x + y = -2
Etter trinnene i sak 1 × 1, studert i forrige seksjon, skriver vi systemet med ligninger på en matrise måte:
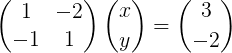 Figur 2. Lineært system i matriseform.
Figur 2. Lineært system i matriseform. Merk at dette systemet er skrevet i kompakt vektornotasjon som følger:
M x = b
hvor
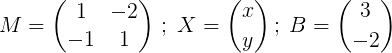
Neste trinn er å finne m.
Metode 1: Gjennom Gaussisk eliminering
Gauss eliminasjonsmetoden vil bli brukt. Som består i å utføre elementære operasjoner på matrisenes rekker, er disse operasjonene:
- Multipliser en rad med et ikke -null -nummer.
- Legg til eller trekke fra en annen rad, eller multiplum av en annen rad.
- Utveksle rader.
Målet er gjennom disse operasjonene å konvertere den opprinnelige matrisen til identitetsmatrisen.
Som dette er gjort, brukes i matrise m nøyaktig de samme operasjonene til identitetsmatrisen. Når det etter flere operasjoner i r -radene blir transformert til enhetsmatrisen, vil den som opprinnelig var enhet, bli omgjort til den omvendte matrisen til M, det vil si m-1.
Kan tjene deg: Corollary (geometri)1- Vi begynner prosessen ved å skrive Matrix M og ved siden av enhetsmatrisen:
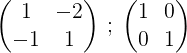
2- Vi legger til de to radene og resultatet blir satt i andre rad, på denne måten får vi et null i det første elementet i den andre raden:
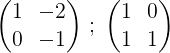
3- Vi multipliserer den andre raden med -1 for å få 0 og 1 i andre rad:
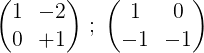
4- Den første raden multipliseres med ½:

5- Den andre og den første legger til, og resultatet er plassert i første rad:
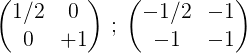
6- For å avslutte prosessen multipliseres den første raden med 2 for å oppnå i den første identitetsmatrisen og i den andre omvendte matrisen til den opprinnelige matrisen M:
Det er å si:
Systemløsning
Når den omvendte matrisen er oppnådd, løses ligningssystemet ved å bruke omvendt matrise i begge medlemmer av den kompakte vektorligningen:
M-1M x = m-1B
X = m-1B
Som eksplisitt forblir slik:
Deretter er matriksmultiplikasjonen gjort for å oppnå vektor x:
Metode 2: ved vedlagt matrise
I denne andre metoden beregnes den omvendte matrisen basert på den vedlagte matrisen til den originale matrisen TIL.
Anta at en matrise gitt av:

hvor du skali, j Det er elementet i rad Yo og kolonnen J av matrisen TIL.
Festing av matrisen TIL Det vil bli kalt Adj (a) Og dets elementer er:
Annonsei, j = (-1)(i+j) ¦Ai, j¦
hvor Ai, j Det er den komplementære mindre matrisen som oppnås ved å eliminere rad I og kolonne J fra den originale matrisen TIL. Stolper ¦ ¦ indikerer at determinanten beregnes, det vil si ¦Ai, j¦ Det er determinanten for den komplementære mindre matrisen.
Kan tjene deg: homologe siderInverse matriseformel
Formelen for å finne den omvendte matrisen basert på den vedlagte matrisen til den originale matrisen er som følger:
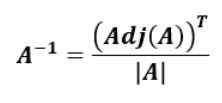
Det vil si den omvendte matrisen til TIL, TIL-1, er transponering av tilknytningen av TIL delt på determinanten av TIL.
Det transponerte TILTav en matrise TIL Det er den som er oppnådd ved å utveksle rekker for kolonner, det vil si den første raden blir den første kolonnen og den andre raden til den andre kolonnen og så videre til N -radene i den originale matrisen.
Trening løst
Vær matrisen til neste:
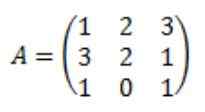
Hver eneste av elementene i den vedlagte matrisen til A: adj (a) beregnes
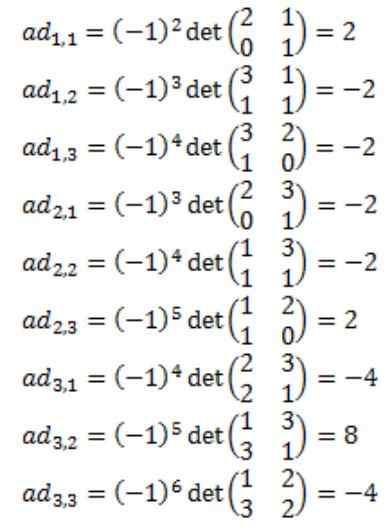
Noe som resulterer i at den vedlagte matrisen til A, adj (a) er som følger:
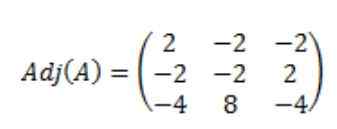
Deretter beregnes determinanten for matrise A, det (a):
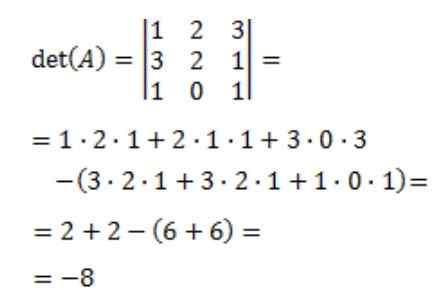
Endelig oppnås den omvendte matrisen til A:
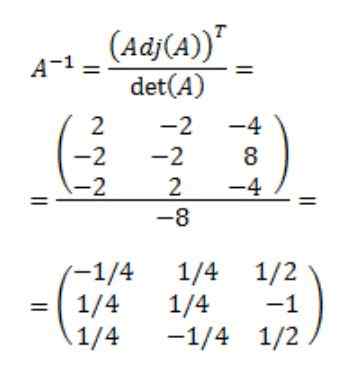
Referanser
- Anthony Nicolaides (1994) Determinanter og matriser. Passpublikasjon.
- Awol Assen (2013) En studie om beregningen av determinantene til 3 × 3
- Casteleiro Villalba m. (2004) Introduksjon til lineær algebra. ESIC -redaksjon.
- Dave Kirkby (2004) Maths Connect. Heinemann.
- Jenny Olive (1998) Maths: A Student's Survival Guide. Cambridge University Press.
- Richard J. Brown (2012) 30-sekunders matematikk: De 50 mest sinnsutvidende teoriene i matematikk. Ivy Press Limited.
- Matrise. Runden Lambert Academic Publishing.

