Treghetsformler, ligninger og eksempler på beregning

Han treghetsmoment Fra et stivt legeme med hensyn til en viss rotasjonsaks, representerer den motstanden mot å endre dens vinkelhastighet rundt den aksen. Det er proporsjonalt med massen og også til plassering av rotasjonsaksen, siden kroppen, i henhold til dens geometri, lettere kan rotere rundt visse akser enn hos andre.

Anta at et omfattende objekt (bestående av mange partikler) som kan rotere rundt en akse. Anta at en styrke handler F, Tangentielt brukt på masseelementet Δm_Yo, som gir et dreiemoment eller øyeblikk, gitt av τ_nett = ∑r_Yo x F_Yo. Vektoren r_Yo Det er posisjonen til Δm_Yo (Se figur 2).

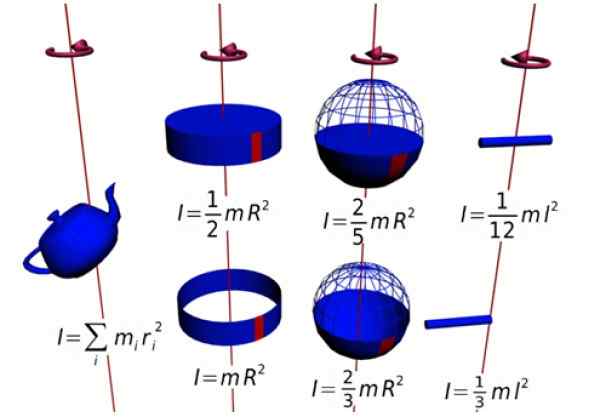
Figur 1. Øyeblikk av treghet av flere figurer. Kilde: Wikimedia Commons.

Dette øyeblikket er vinkelrett på rotasjonsplanet (adresse +K = forlater papir). Siden styrken og radialposisjonen alltid er vinkelrett, gjenstår kryssproduktet:

τ_nett = ∑ f_Yo r_Yo k = ∑ (Δm_Yo til_Yo) r_Yo  k = ∑ Δm_Yo (til_Yo r_Yo ) k

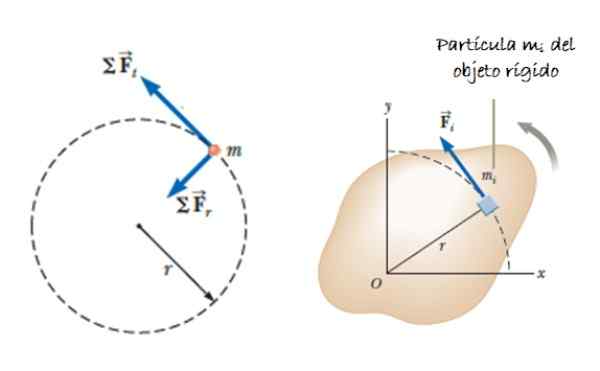Figur 2. En partikkel som tilhører et stivt fast stoff i rotasjon. Kilde: Serway, R. 2018. Fysikk for vitenskap og ingeniørfag. Volum 1. Cengage Learning.

Akselerasjon a_Yo representerer den tangensielle komponenten i akselerasjon, siden radial akselerasjon ikke bidrar til dreiemoment. Avhengig av vinkelakselerasjon α, kan vi indikere at:

til_Yo = α r_Yo

Derfor er nettomomentet slik:

τ_nett = ∑ Δm_Yo (α r_Yo²) K = (∑ r_Yo² Δm_Yo) α k

Vinkelakselerasjon α er den samme for hele objektet, derfor påvirkes det ikke av abonnementet "I" og kan forlate summen, som nettopp er treghetsmomentet til det symboliserte objektet med bokstaven I:

I = ∑ r_Yo² Δm_Yo

Dette er treghetsmomentet for en diskret massedistribusjon. Når distribusjonen er kontinuerlig, erstattes summen med en integrert og Δm blir en massedifferensial DM. Integralen er gjort fremfor alt objektet:

I = ∫_M(r²) DM

Enhetene for treghetsmomentet i det internasjonale systemet hvis de er kg x m². Det er en skalær og positiv mengde, siden det er produktet av en deig av torget på en avstand.

[TOC]

Eksempler på beregning

Et utvidet objekt, for eksempel en stolpe, plate, sfære eller annen, hvis tetthet ρ Det er konstant og å vite at tetthet er massevolumkvoten, massedifferensialet DM Det er skrevet som:

ρ = dm/dv → dm = ρDv

Erstatt i integralen for treghetsmomentet, har vi:

I = ∫r² ρdv = ρ ∫r²Dv

Dette er et generelt uttrykk, gyldig for et tredimensjonalt objekt, hvis volum V og posisjon r De er funksjoner av romkoordinater x, og og z. Legg merke til at å være konstant, tettheten er ute av integralen.

Tettheten ρ Det er også kjent som volumetrisk tetthet, men hvis objektet er veldig flatt, som et ark eller veldig tynt og smalt som en stang, kan andre former for tetthet brukes, la oss se:

Kan tjene deg: jordens rotasjonsbevegelse

- For et veldig fint ark er tettheten som skal brukes σ, overflatetettheten (masse per arealenhet) og gir er områdets differensial.

- Og hvis det er en tynn stang, der bare lengden er relevant, brukes lineær massetetthet λ og en lengdedifferensial, i henhold til aksen som ble brukt som referanse.

I de følgende eksemplene anses alle objekter som stive (ikke -avformbare) og har ensartet tetthet.

Treghetsmoment av en tynn stang med hensyn til en akse som passerer gjennom sentrum

Her skal vi beregne treghetsmomentet til en tynn, stiv, homogen stang, av lengde L og masse m, med hensyn til en akse som passerer gjennom midlene.

For det første er det nødvendig å etablere et koordinatsystem og bygge en figur med tilstrekkelig geometri, for eksempel dette:

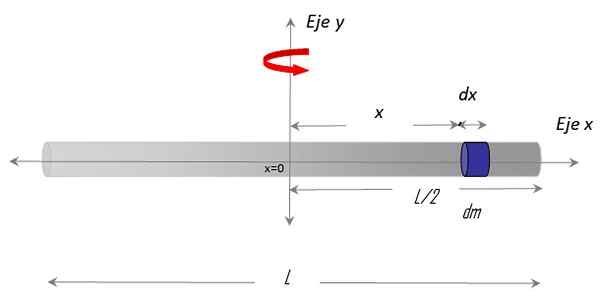Figur 3. Geometri for å beregne treghetsmomentet til en tynn stang med hensyn til en vertikal akse som passerer gjennom sentrum. Kilde: f. Zapata.

Han ble valgt X akse langs baren og Axis y som rotasjonsakse. Prosedyren for å etablere integral krever også å velge en massedifferensial på baren, kalt DM, som har en differensiallengde Dx og ligger i stillingen x vilkårlig, med hensyn til sentrum x = 0.

I henhold til definisjonen av lineær massetetthet λ:

λ = m/l

Når tettheten er ensartet, som er gyldig for M og L, er det også for DM og DX:

λ = dm/dx → dm = λdx.

På den annen side er masseelementet i posisjon x, Ved å erstatte denne geometrien i definisjonen, har vi et bestemt integral, hvis grenser er ytterpunktene i stangen i henhold til koordinatsystemet:

Erstatte lineær tetthet λ = m/l:

For å finne treghetens øyeblikk med hensyn til en annen rotasjonsakse, for eksempel en som passerer gjennom et av den Vist her, men riktig modifiserende geometri.

Treghetsmoment av et album med hensyn til en akse som går gjennom sentrum

Et veldig tynt album, med foraktelig tykkelse er en flat figur. Hvis deigen er jevnt fordelt over hele området A, er massetetthet σ:

σ = M/a

Så mye DM som gir Samsvarer med massen og området for differensialringen vist på figuren. Vi vil anta at hele settet dreier seg om aksen og.

Du kan forestille deg at albumet er komponert for at mange radiokonsentriske ringer r, hver med sitt respektive treghetsøyeblikk. Legger til bidragene fra alle ringer til du kommer til radioen R, Du vil ha den totale tregheten til albumet.

σ = DM/DA → DM = σgir

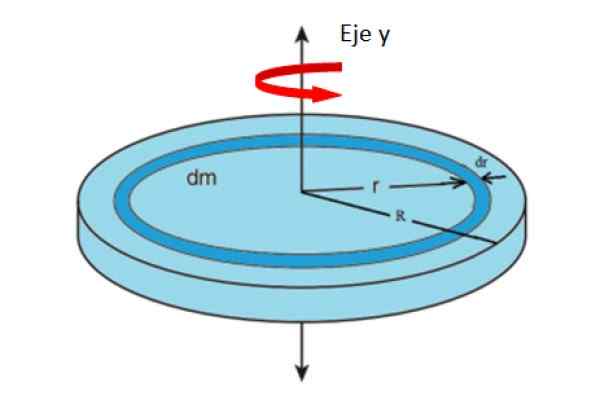Figur 4. Geometri for å beregne treghetsmomentet til et album, med hensyn til den aksiale aksen. Kilde: f. Zapata.

Hvor M representerer hele albumets deig. Området til et album avhenger av radius r som:

Kan tjene deg: hastigheten på forplantning av en bølge

A = π.r²

Stammer om r:

Da /dr = 2 = 2π.R → da = 2π.rdr

Erstatte ovennevnte i definisjonen av i:

Etter å ha evaluert de integrerte resultatene:

Erstatning σ = m/(π.R² ) er til overs:

Treghetsmoment av en solid sfære med hensyn til en diameter

En radius r sfære kan betraktes som en serie stablede plater oppå hverandre, der hvert uendelig massealbum DM, radio r og tykkelse Dz, Det har et øyeblikk av treghet gitt av:

ga_disk = (½) r²DM

For å finne denne differensialen ble formelen for forrige seksjon ganske enkelt tatt og erstattet M og R av DM og r, henholdsvis. Et album som dette kan sees i geometrien i figur 5.

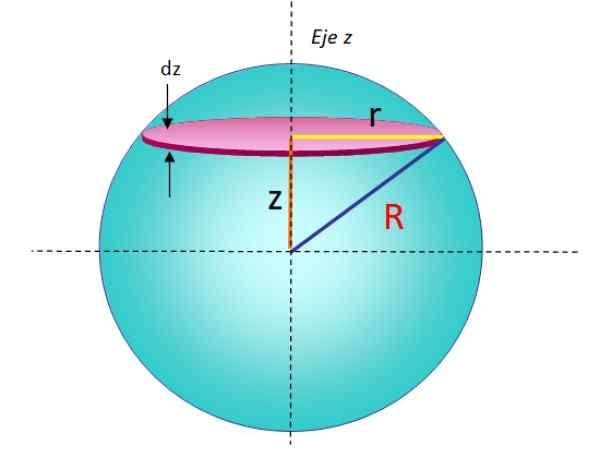Figur 5. Geometri for å beregne treghetsmomentet til en fast radiusfære med hensyn til en akse som passerer gjennom en diameter. Kilde: f. Zapata.

Ved å legge til alle øyeblikk med uendelig treghet av stablede plater, oppnås øyeblikket av total treghet av sfæren:

Yo_sfære = ∫di_disk

Som tilsvarer:

I = ∫_sfære (½) r²DM

For å løse integralen, må du uttrykke DM ordentlig. Som alltid oppnås det fra tetthet:

ρ = m/v = dm/dv → dm = ρ.Dv

Volumet til en differensialskive er:

DV = baseareal x høyde

Høyden på albumet er tykkelsen Dz, Mens basisområdet er πr², derfor:

DV = πr²Dz

Og å erstatte den integrerte ville være slik:

I = ∫_sfære(½) r²Dm = ∫ (½) r²(ρπr²Dz)

Men før det integrerer seg, må det. Gjennom Pythagoras -teoremet:

R² = r² + z² → R² = R² - z²

 Det fører oss til:

I = ∫_sfære(½) ρ r²(πr²dz) = ∫_sfære(½) ρ π r⁴Dz= ∫_sfære(½) ρ π (r² - z²)² Dz

For å integrere hele sfæren, merker vi at Z varierer mellom -r og R, derfor:

Vet det ρ = m/v = m/[(4/3) πr³] Til slutt oppnås det, etter å ha forenklet:

Treghetsmoment av en fast sylinder med hensyn til aksialaksen

For dette objektet brukes en metode som ligner den som brukes for sfæren, bare denne gangen er det lettere hvis sylinderen er tenkt for radiosylindriske skjell r, tykkelse Dr og høyde H, Som om de var lagene på en løk.

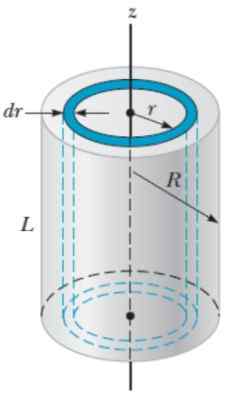Figur 6. Geometri for å beregne treghetsmomentet til en fast radius sylinder r respekt for den aksiale aksen. Kilde: Serway, R. 2018. Fysikk for vitenskap og ingeniørfag. Volum 1. Cengage.

Volumet Dv av et sylindrisk lag er:

DV = 2π.Rl.Dr

Derfor er Cascaron -massen:

Kan tjene deg: Mikroskopisk skala: egenskaper, tellepartikler, eksempler

Dm = ρ.DV = ρ. 2π.r.L.Dr

Dette uttrykket erstattes i definisjonen av treghetsmoment:

 Gitt at ρ = m / (π.R²L) er til overs:

Den forrige ligningen indikerer at sylinderens øyeblikk ikke er avhengig av dens lengde, men av dens masse og dens radius. Ja L endret, treghetsmomentet med hensyn til den aksiale aksen vil fortsette å være det samme. Av denne grunn, Yo av sylinderen sammenfaller med den fra det tidligere beregnede tynne albumet.

Treghetsmoment av et rektangulært ark med hensyn til en akse som passerer gjennom sentrum

De Axis y Horisontalt som en rotasjonsaks. Figuren nedenfor viser nødvendig geometri for å utføre integrasjon:

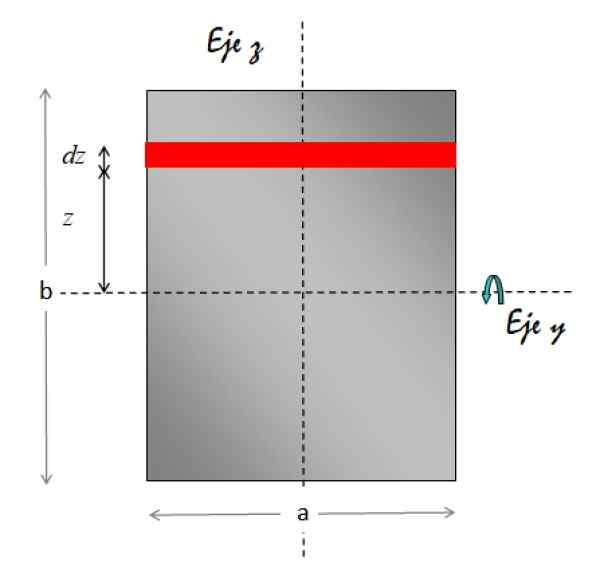Figur 7. Geometri for beregning av treghetsmomentet til en rektangulær plate med hensyn til en parallell akse til arket og som passerer gjennom sentrum. Kilde: f. Zapata.

Områdeelementet angitt i rødt er rektangulært. Området er base x høyde, derfor:

da = a.Dz

Derfor er massedifferensialet:

Dm = σ.da = σ.(til.Dz)

Når det gjelder avstanden til områdeelementet til rotasjonsaksen, er det alltid z. Vi erstatter alt dette i integralen av treghetsmomentet:

Nå erstattes overflatemassetetthet σ av:

σ = m/ab

Og det er definitivt slik:

Merk at det er som den tynne stangen.

Treghetsmoment av et firkantet ark med hensyn til en akse som passerer gjennom sentrum

For en firkant på siden L, I forrige uttrykk gyldig for et rektangel, verdien av b av den ene L:

Teoremer om treghetens øyeblikk

Det er to spesielt nyttige teoremer for å forenkle beregningen av treghetsmomenter med hensyn til andre akser, som ellers kan være komplisert å finne for mangelen på symmetri. Disse teoremene er:

Steiner's teorem

Også kalt Parallell akse teorem, relaterer treghetens øyeblikk angående en akse med en annen som passerer gjennom objektets massesenter, så lenge aksene er parallelle. For å bruke den, må avstanden d være kjent mellom de to aksene og selvfølgelig massen m av objektet.

Være Yo_z treghetsmomentet til et utvidet objekt med hensyn til Z, I Axis_CM Treghetsmomentet med hensyn til en akse som passerer gjennom massesenteret (CM) til nevnte objekt, så blir det oppfylt at:

Yo_z = Jeg_CM + MD²

Eller i notasjonen av følgende figur: Yo_{z '} = Jeg_z + MD²

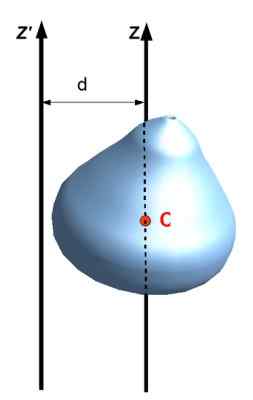Figur 8. Steiner teorem eller parallelle akser. Kilde: Wikimedia Commons. Jack Se [CC By-SA (https: // CreativeCommons.Org/lisenser/by-SA/3.0)]

Vinkelrett akse -teorem

Dette teoremet gjelder flate overflater og sier: treghetsmomentet til en flat gjenstand rundt en akse vinkelrett på det er summen av treghetsmomentene rundt to akser vinkelrett på den første aksen:

Yo_z = Jeg_x + Yo_og

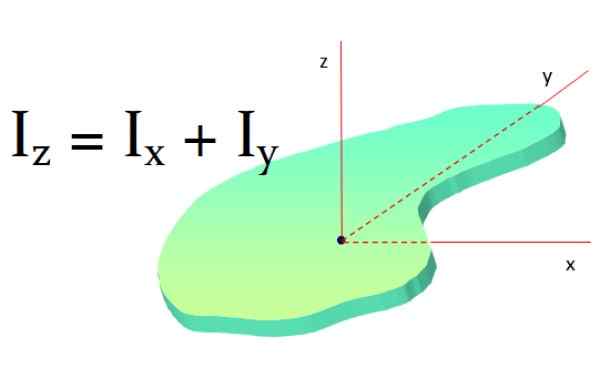Figur 9. Vinkelrett akse -teorem. Kilde: f. Zapata.

Hvis objektet har symmetri slik at Yo_x og Yo_og De er de samme, så blir det oppfylt at:

Yo_z = 2i_x

Trening løst

Finn treghetens øyeblikk med hensyn til en akse som passerer gjennom en av dens ender, for eksempel den vist i figur 1 (nedenfor og til høyre) og figur 10.

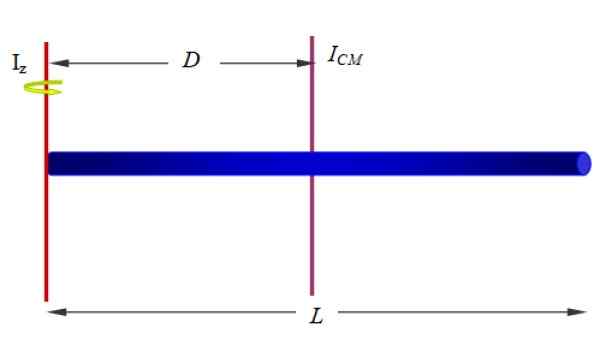Figur 10. Treghetsmoment av en homogen bar rundt en akse som går gjennom den ene enden. Kilde: f. Zapata.

Løsning:

Vi har allerede treghetsmomentet til baren rundt en akse som passerer gjennom dets geometriske sentrum. Siden baren er homogen, er massesenteret på det tidspunktet, så dette vil være vårt Yo_CM Å bruke Steiner's teorem.

Hvis lengden på baren er L, Z -aksen er på avstand d = l/2, derfor:

Yo_z = Jeg_CM + MD²= (1/12) ML²+M (l/2)²= (1/3) ML²

Referanser

1. Bauer, w. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill. 313-340
2. Rex, a. 2011. Fundamentals of Physics. Pearson. 190-200.
3. Parallell akse teorem. Gjenopprettet fra: hyperfysikk.PHY-ASTR.GSU.Edu.
4. Serway, r. 2018. Fysikk for vitenskap og ingeniørfag. Volum 1. Cengage.
5. Sevilla University. Treghetsmoment av sfæriske faste stoffer. Gjenopprettet fra: Laplace.oss.er.
6. Sevilla University. Treghetsmoment av et partikkelsystem. Gjenopprettet fra: Laplace.oss.er.
7. Wikipedia. Parallell akse teorem. Hentet fra: i.Wikipedia.org