Rektilinære bevegelsesegenskaper, typer og eksempler

Han Rektilineal bevegelse Det er en der mobilen beveger seg langs en rett linje og derfor passerer i en dimensjon, og mottar derfor også navnet på Unidimensjonal bevegelse. Denne rette linjen er bane eller sti etterfulgt av objektet som beveger seg. Bilene som reiser langs muligheten til figur 1 følger denne typen bevegelser.

Dette er den enkleste bevegelsesmodellen som kan tenkes. De daglige bevegelsene til mennesker, dyr og ting kombinerer ofte overføringer i en rett linje med bevegelser langs kurver, men noen observerer ofte noen som utelukkende er rektilineale.

Figur 1. Biler som beveger seg langs en rettlinjig aveny. Kilde: Pixabay.

Her er noen gode eksempler:

- Når du løper langs et rettlinjet spor på 200 meter.

- Kjører en bil på en rett vei.

- Slippe et objekt fritt fra en viss høyde.

- Når en ball kastes vertikalt.

https: // giphy.com/gifs/j5xx3bynaqv06wtoxq

Nå oppnås målet med å beskrive en bevegelse ved å spesifisere egenskaper som:

- Posisjon

- Forskyvning

- Hastighet

- Akselerasjon

- Tid.

For at en observatør skal oppdage bevegelsen av et objekt, er det nødvendig å ha et referansepunkt (opprinnelse O) og har etablert en spesifikk adresse hvor man skal bevege seg, som kan være aksen x, aksen og eller noe annet.

Når det gjelder objektet som beveger seg, kan dette ha utallige måter. Det er ingen begrensninger i denne forbindelse, men i alt som følger vil det antas at mobilen er en partikkel; et objekt så lite at dimensjonene ikke er relevante.

Det er kjent at dette ikke er tilfelle for makroskopiske gjenstander; Imidlertid er det en modell med gode resultater i beskrivelsen av den globale bevegelsen til et objekt. På denne måten kan en partikkel være en bil, en planet, en person eller noe annet objekt som beveger seg.

Vi vil begynne vår studie av rettlinjede kinematikk med en generell tilnærming til bevegelsen, og deretter vil spesielle tilfeller bli studert som de som allerede er utnevnt.

[TOC]

Generelle kjennetegn ved den rettlinjede bevegelsen

Følgende beskrivelse er generell og anvendelig for alle typer en -dimensjonal bevegelse. Den første tingen er å velge et referansesystem. Linjen som bevegelsen finner sted vil være aksen x. Parametrene for bevegelsen:

Posisjon

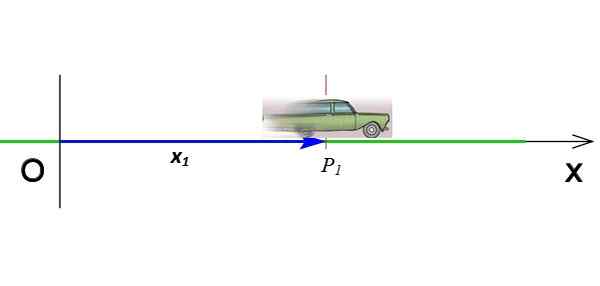Figur 2. Plassering av en mobil som beveger seg på x -aksen. Kilde: Wikimedia Commons (modifisert av f. Zapata).

Det er vektoren som går fra opprinnelsen til det punktet hvor objektet er på et øyeblikk gitt. I figur 2, vektoren x₁ Indikerer mobilens plassering når den er i koordinaten P₁ Og i tide t₁. Posisjonsvektorenhetene i det internasjonale systemet er meter.

Forskyvning

Forskyvning er vektoren som indikerer endringen i posisjon. I figur 3 har bilen gått fra stillingen P₁ til stillingen P₂, Derfor er forskyvningen Δx = x₂ - x₁. Forskyvning er subtraksjon av to vektorer, den symboliseres med den greske bokstaven Δ ("Delta") og er igjen en vektor. Enhetene i det internasjonale systemet er meter.

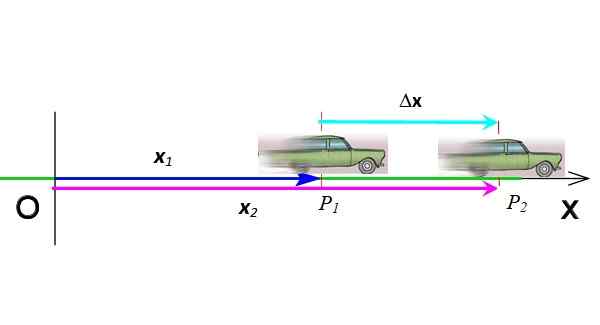Figur 3. Vektorforskyvning. Kilde: Utarbeidet av F. Zapata.

Vektorer er betegnet med fet skrift i trykt tekst. Men å være på samme dimensjon, hvis ønskelig kan du gjøre uten vektornotasjonen.

Kan tjene deg: grener av klassisk og moderne fysikk

Avstand reist

Avstand d Turned av det bevegelige objektet er den absolutte verdien av forskyvningsvektoren:

D = ΙxΙ = Δx

Å være en absolutt verdi, er avstanden alltid større enn eller lik 0, og enhetene er den samme som for posisjon og forskyvning. Absolutt verdinotasjon kan gjøres med modulstenger eller bare fjerne den dristige bokstaven i trykt tekst.

Gjennomsnittshastighet

Hvor raskt endres stillingen? Det er trege og raske mobiltelefoner. Nøkkelen har alltid vært hastigheten. For å analysere denne faktoren blir posisjonen analysert x Tidens funksjon t.

Gjennomsnittshastigheten v_m (Se figur 4) Det er skråningen på tørkelinjen (fuchsia) til kurven x vs t og gir global informasjon om mobil forskyvning i tidsintervallet som vurderes.

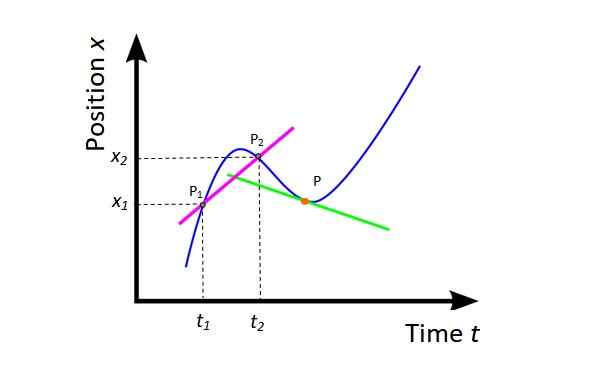Figur 4. Gjennomsnittshastighet og øyeblikkelig hastighet. Kilde: Wikimedia Commons, modifisert av f. Zapata.

v_m = (x₂ - x₁) / (t₂ -t₁) = Δx / Δt

Gjennomsnittshastigheten er en vektor hvis enheter i det internasjonale systemet er meter /sekund (m/s).

Øyeblikkelig hastighet

Gjennomsnittshastigheten beregnes ved å ta et målbart tidsintervall, men informerer ikke om hva som skjer innenfor nevnte intervall. For å kjenne hastigheten når som helst, må du gjøre tidsintervallet veldig lite, matematisk tilsvarer det å gjøre:

ΔT → 0

Ligningen er tidligere gitt for gjennomsnittshastighet. På denne måten oppnås øyeblikkelig hastighet eller ganske enkelt hastighet:

Geometrisk er derivatet av posisjonen med hensyn til tid skråningen på linjen tangens til kurven x vs t på et gitt punkt. I figur 4 er punktet oransje og tangentlinjen er grønn. Den øyeblikkelige hastigheten på dette tidspunktet er skråningen på den linjen.

Hastighet

Hastighet er definert som den absolutte verdien eller hastighetsmodulen og er alltid positiv (signalering, veier og motorveier er alltid positive, aldri negative). Begrepene "hastighet" og "hastighet" kan brukes daglig, men i fysikk er skillet mellom vektor og klatring nødvendig.

v = ΙvΙ = v

Gjennomsnittlig akselerasjon og øyeblikkelig akselerasjon

Hastigheten kan endre seg i løpet av bevegelsen, og realiteten er at den forventes å gjøre det. Det er en størrelse som kvantifiserer denne endringen: akselerasjon. Hvis vi merker at hastighet er endring av posisjon med hensyn til tid, er akselerasjon endring av hastighet med hensyn til tid.

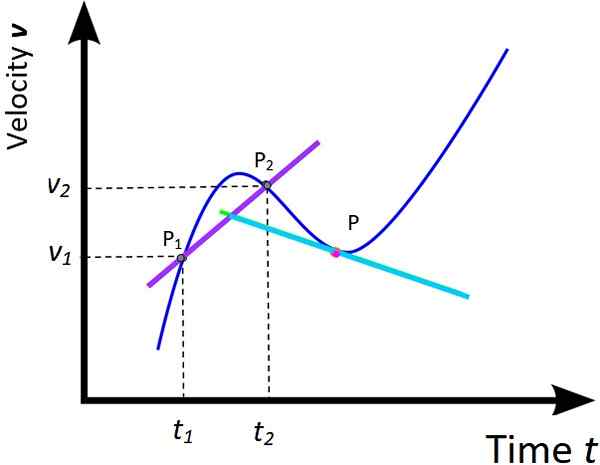Figur 5. Gjennomsnittlig akselerasjon og øyeblikkelig akselerasjon. Kilde: Wikimedia Commons, modifisert av f. Zapata.

Behandlingen gitt til grafen til x vs t av de to foregående seksjonene kan utvides til den tilsvarende grafen til v vs t. Følgelig er en gjennomsnittlig akselerasjon og øyeblikkelig akselerasjon definert som:

til_m = (v₂ - v₁) / (t₂ -t₁) = Δv / Δt  (I påvente av bolig)

Akselerasjon og retardasjon

I den endimensjonale bevegelsen har vektorer etter konvensjon positive eller negative tegn når de går på en eller annen måte. Når akselerasjonen har samme betydning som hastigheten, øker den størrelsen, men når den gir motsatt mening og hastigheten reduserer størrelsen. Det sies da at bevegelsen er forsinket.

Kan tjene deg: Leyden flaske: Deler, drift, eksperimenter

Folkens

Klassifiseringen av rektilinesiske bevegelser gjøres vanligvis basert på:

- Om akselerasjonen er konstant eller ikke.

- Bevegelsen passerer langs en horisontal eller vertikal linje.

Bevegelse med konstant akselerasjon

https: // giphy.com/gifs/ylzfnbidhm7rp391fi

Når akselerasjonen er konstant, er gjennomsnittlig akselerasjon til_m Det er lik øyeblikkelig akselerasjon til Og det er to alternativer:

- At akselerasjonen er verdt 0, i så fall er hastigheten konstant og har en jevn rettlinjet bevegelse eller MRU.

- Konstant akselerasjon forskjellig fra 0, der hastigheten vokser eller reduseres lineært over tid (den rettlinjede bevegelsen enhetlig variert eller MRUV):

Hvor v_F  og t_F De er henholdsvis endelig hastighet og tid, og v_enten og t_enten De er innledende hastighet og tid. Ja t_enten = 0, Når du rydder den endelige hastigheten, har du ligningen som allerede er kjent for den endelige hastigheten:

v_F = v_enten + PÅ

For denne bevegelsen er følgende ligninger også gyldige:

- Posisjon avhengig av tid: x = x_enten + v_{enten .}T +½ på²

- Hastighet avhengig av stillingen: v_F² = v_enten² + 2.Δx  (Med Δx = x - x_enten)

Horisontale bevegelser og vertikale bevegelser

De horisontale bevegelsene er de som passerer langs den horisontale aksen eller x -aksen, mens de vertikale gjør det langs aksen og aksen. Vertikale bevegelser under tyngdekraften er de hyppigste og interessante.

I de forrige ligningene blir det tatt A = g = 9.8 m/s² rettet vertikalt ned, retning som nesten alltid er valgt med et negativt tegn.

Denne måten, v_F = v_enten + PÅ Det forvandler seg inn v_F = v_enten - Gt Og hvis den opprinnelige hastigheten er 0 fordi objektet ble droppet fritt, er den ytterligere forenklet til v_F = - gt. Så lenge luftmotstand ikke tas i betraktning, selvfølgelig.

Løste eksempler

Eksempel 1

På punktet frigjøres en liten pakke slik at den beveger seg langs transportøren med skyvehjul ABCD vist på figuren. Mens du synker gjennom skrå seksjoner AB og CD, bærer pakken en akselerasjon på 4,8 m/s², Mens du er i den horisontale delen, opprettholder BC konstant hastighet.

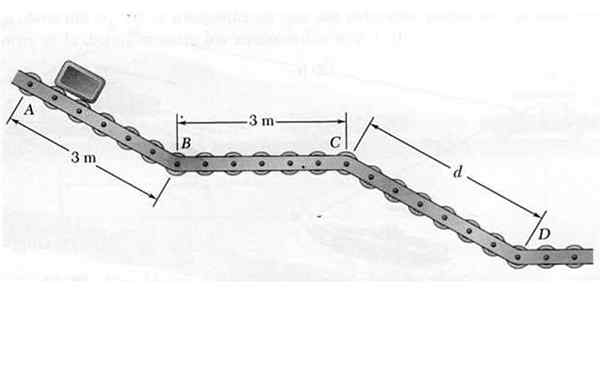Figur 6. Pakken som beveger seg på skyvestien til det løste eksemplet 1. Kilde: Selvlaget.

Å vite at hastigheten som pakken på D er når er 7,2 m/s, bestem:

a) Avstanden mellom C og D.

b) Tiden som kreves for at pakken skal nå slutten.

Løsning

Bevegelsen av pakken utføres i de tre rettlinjede seksjonene som er vist og for å beregne de forespurte, er hastigheten påkrevd på punkt B, C og D. La oss analysere hver seksjon hver for seg:

Avsnitt AB

Siden tiden ikke er tilgjengelig i denne delen, vil den bli brukt v_F² = v_enten² + 2.Δx  Med vo = 0:

v_F² = 2a.Δx → v_F²= 2. 4,8 m/s² . 3 m = 28.8 m²/s² → v_F  = 5.37 m/s = v_B

Tiden som pakken tar for å reise seksjonen AB er:

t_AB = (v_F - v_enten) /A = 5.37 m/s/4,8 m/s² = 1.19 s

Avsnitt BC

Hastigheten i seksjon BC er konstant, derfor v_B = v_C = 5.37 m/s. Tiden det tar for pakken å reise denne delen er:

Kan tjene deg: Lett refraksjon: elementer, lover og eksperiment

t_BC = avstand _BC  / v_B = 3 m/ 5.37 m/s = 0.56 s

CD -seksjon

Den første hastigheten på denne delen er v_C = 5.37 m/s, Den endelige hastigheten er v_D = 7,2 m/s, via v_D²  = v_C² + 2. til. d Verdien av d:

D = (v_D²  - v_C²)/2.a = (7.2²  - 5.37²)/2 x 4.8 m = 2.4 m

Tiden beregnes som:

t_{CD =} (v_D  - v_C)/A = (7.2- 5.37)/ 4.8 S = 0.38 s.

Svarene på spørsmålene som er reist er:

a) d = 2.4 m

b) Reisetid er t_AB + t_BC + t_CD = 1.19 S +0.56 S +0.38 S = 2.13 s.

Eksempel 2

En person er under en horisontal port som opprinnelig er åpen og 12 m høy. Personen lanserer vertikalt et objekt mot porten med 15 m/s hastighet.

Det er kjent at porten lukkes 1,5 sekunder etter at personen har lansert gjenstanden fra en høyde på 2 meter. Luftmotstand vil ikke bli tatt i betraktning. Svar på følgende spørsmål, rettferdiggjør:

a) Klarer du å passere objektet gjennom porten før det stenger?

b) Vil objektet noen gang kollidere mot den lukkede porten? Hvis bekreftende, når skjer det?

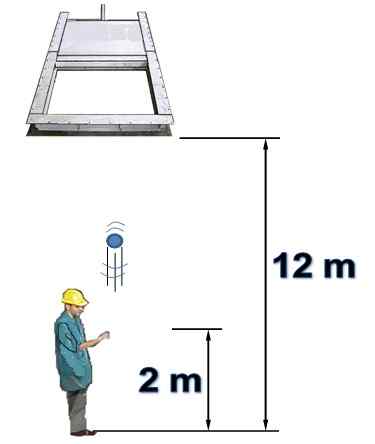Figur 7. Et objekt lanseres vertikalt opp (løst eksempel 2). Kilde: Selvlaget.

Svar til)

Det er 10 meter mellom startposisjonen til ballen og porten. Det er en vertikal lansering, der denne adressen blir tatt som positiv.

Du kan finne ut hastigheten den bærer når du ankommer til dette punktet, med dette resultatet tiden det vil ta å gjøre det og sammenligne det med stengetid for porten, som er 1.5 sekunder:

v_F ²= v_enten ²- 2.g. Δog → v_F = (15² - 2 x 9.8 x10)^1/2 m = 5.39 m/s

T = (v_F - v_enten) /g = (5.39 - 15) / (-9.8) S = 0.98 s

Siden denne gangen er mindre enn 1.5 sekunder, da konkluderes det med at objektet kan gå gjennom porten minst en gang.

Svar b)

Vi vet allerede at objektet klarer seg. Hastigheten, når den når på høyden av porten, har samme størrelse som når den går opp, men i motsatt retning. Arbeid derfor med -5.39 m/s og tiden det tar å nå denne situasjonen er:

T = (v_F - v_enten) /G = (-5.39 - 15) / (-9.8) S = 2.08 s

Ettersom porten bare forblir åpen for 1.5 S, det er tydelig at den ikke har tid til å passere før den stenger, siden den finner den lukket. Svaret er: objektet hvis det kolliderer med den lukkede porten etter 2.08 sekunder etter å ha blitt utgitt, når det kommer i nedstigning.

Referanser

1. Figueroa, d. (2005). Serier: Fysikk for vitenskap og ingeniørfag. Volum 1. Kinematikk. Redigert av Douglas Figueroa (USB).69-116.
2. Giancoli, d. Fysikk. (2006). Prinsipper med applikasjoner. 6^th Utgave. Prentice Hall. 22-25.
3. Kirkpatrick, l. 2007. Fysikk: En titt på verden. 6^ta Forkortet utgave. Cengage Learning. 23 - 27.
4. Resnick, r. (1999). Fysisk. Volum 1. Tredje utgave på spansk. Mexico. Continental Editorial Company s.TIL. Av c.V. 21-22.
5. Rex, a. (2011). Fundamentals of Physics. Pearson. 33 - 36
6. Sears, Zemansky. 2016. Universitetsfysikk med moderne fysikk. 14^th. Ed. Volum 1. 50 - 53.
7. Serway, r., Jewett, J. (2008). Fysikk for vitenskap og ingeniørfag. Volum 1. 7^ma. Utgave. Mexico. Cengage Learning Editors. 23-25.
8. Serway, r., Vulle, c. (2011). Fundamentals of Physics. 9^na Ed. Cengage Learning. 43 - 55.
9. Wilson, J. (2011). Fysikk 10. Pearson Education. 133 - 149.