Ensartede rettlinjede bevegelsesegenskaper, formler, øvelser

Han Ensartet linjebevegelse eller med konstant hastighet er en der partikkelen beveger seg langs en rett linje og med konstant hastighet. På denne måten reiser mobilen like avstander i like tider. For eksempel, hvis det på 1 sekund reiser 2 meter, vil det etter 2 sekunder være 4 meter og så videre.

For å lage en nøyaktig beskrivelse av bevegelsen, enten det er ensartet rettlinjet eller noe annet, er det nødvendig å etablere et referansepunkt, også kalt opprinnelse, angående hvilken mobil endrer stilling.

Figur 1. En bil som beveger seg langs en rettlinjet vei med konstant hastighet har ensartet rettlinjet bevegelse. Kilde: Pixabay.

Hvis bevegelsen passerer helt langs en rett linje, er den også interessert i å vite i hvilken forstand mobilen reiser.

På en horisontal linje er det mulig at mobilen går til høyre eller til venstre. Skillet mellom de to situasjonene er gjort av tegn, og følgende er følgende: Til høyre følger jeg (+) og til venstre skilt (-).

Når hastigheten er konstant, endrer ikke mobilen sin retning eller dens betydning, og også størrelsen på hastigheten forblir uendret.

[TOC]

Kjennetegn

Hovedegenskapene til den ensartede rettlinjede bevegelsen (MRU) er følgende:

-Bevegelsen passerer alltid langs en rett linje.

-En mobil med MRU reiser like avstander eller mellomrom i like tider.

-Hastigheten forblir uforanderlig både i størrelse og retning.

-MRU mangler akselerasjon (det er ingen hastighetsendringer).

-Siden hastighet v forblir konstant over tid t, Grafen med størrelsesorden som en funksjon av tid er en rett linje. I eksemplet på figur 2 er linjen grønn og verdien av hastigheten leses på den vertikale aksen, omtrent +0.68 m/s.

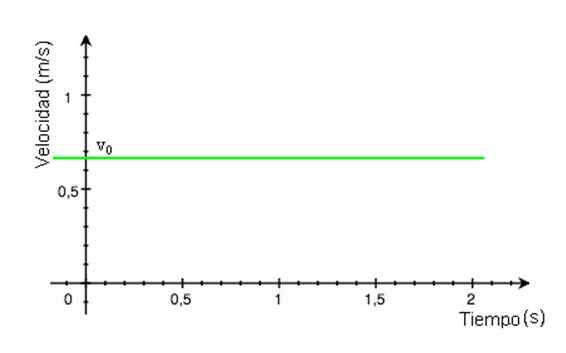Figur 2. Hastighetsgraf avhengig av en MRU. Kilde: Wikimedia Commons.

-Grafen til X -posisjonen med hensyn til tid er en rett linje, hvis skråning tilsvarer mobilhastighet. Hvis X vs T -graflinjen er horisontal, er mobilen i ro, hvis skråningen er positiv (graf i figur 3), er hastigheten også.

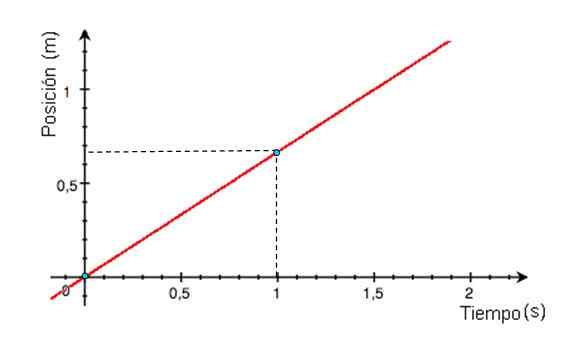Figur 3. Graf over posisjonen som en funksjon av tiden for en mobil med MRU som gikk fra opprinnelsen. Kilde: Wikimedia Commons.

Avstand reist fra graf V vs. t

Kjenn avstanden som blir reist av mobilen når grafen er tilgjengelig V Vs. T er veldig enkelt. Den tilbakelagte avstanden tilsvarer området under linjen og inkludert i ønsket tidsintervall.

Det kan tjene deg: Gjennomsnittlig akselerasjon: Hvordan den beregnes og løses

Anta at du vil vite avstanden som er reist av mobilen til figur 2 i intervallet mellom 0.5 og 1.5 sekunder.

Dette området er det av det skyggelagte rektangelet i figur 4. Det beregnes ved å finne resultatet av å multiplisere basen av rektangelet med høyden, hvis verdier blir lest fra grafikken.

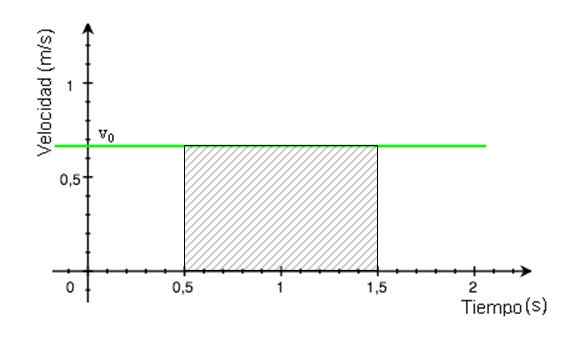Figur 4. Det stripete området tilsvarer den tilbakelagte avstanden. Kilde: Modified Wikimedia Commons.

Avstand reist = (1.femti.5) x 0.68 m = 0.68 m

Avstanden er alltid en positiv mengde, uavhengig av om du går til høyre eller til venstre.

Formler og ligninger

I MRU er gjennomsnittshastigheten og øyeblikkelig hastighet alltid den samme, og siden verdien er hellingen til graf X vs t som tilsvarer en linje, er de tilsvarende ligningene avhengig av tiden følgende:

-Posisjon avhengig av tid: x (t) = x_enten + Vt

x_enten Det representerer den opprinnelige posisjonen til mobilen, ved mange anledninger sammenfaller den med referansesystemets opprinnelse, men det er ikke alltid slik. Denne ligningen er også kjent som Reiserute ligning.

-Hastighet avhengig av tid: v (t) = konstant

Når v = 0 betyr at mobilen er hvile. Hvil er et spesielt tilfelle av bevegelse.

-Akselerasjon som en funksjon av tiden: A (t) = 0

I den ensartede rettlinjede bevegelsen er det ingen hastighetsendringer, derfor er akselerasjonen null.

Løste øvelser

På tidspunktet for å løse en øvelse, bør det sikres at situasjonen tilsvarer modellen som skal brukes. Spesielt før du bruker MRU -ligningene er det nødvendig å sørge for at de er aktuelle.

Følgende øvelser løst er to mobile problemer.

Trening løst 1

To idrettsutøvere nærmer seg hverandre med konstant hurtighet på 4.50 m/s og 3.Henholdsvis 5 m/s, og ble opprinnelig separert en avstand på 100 meter, som indikert i figuren.

Hvis hver og en opprettholder sin konstante hastighet, finn: a) Hvor lang tid tar det å møtes? b) Hva vil være posisjonen til hver på den tiden?

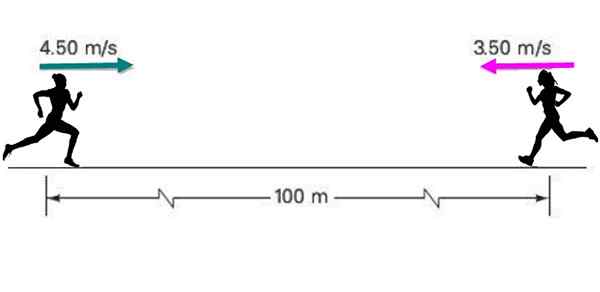Figur 5. To løpere flytter til hverandre konstant. Kilde: Selvlaget.

Løsning

Den første er å indikere opprinnelsen til koordinatsystemet som vil tjene som referanse. Valget avhenger av preferansen som personen som løser problemet har.

Kan tjene deg: Hva er volumetrisk utvidelse? (Med eksempler)

Det er vanligvis valgt x = 0 til høyre ved startpunktet for mobiltelefoner, det kan være i løperen til venstre eller høyre, det kan til og med velges midt i begge.

a) Vi skal velge x = 0 på løperen av venstre eller løper 1, derfor er startposisjonen til dette x₀₁ = 0 og for løper 2 vil være x₀₂ = 100 m. Megler 1 beveger seg fra venstre til høyre med hastighet v₁ = 4.50 m/ mens løper 2 gjør det fra høyre til venstre med hastighet på -3.50 m/s.

Bevegelsesligning for den første megleren

x₁ = x₀₁ + v₁t₁ = 4.50t₁

Bevegelsesligning for den andre megleren

x₂ = x₀₂ + v₂t₂ = 100 -3.50t₂

Som tiden er den samme for begge t₁ = t₂ = t , Når begge posisjonene vil være den samme, derfor x₁ = x₂. Lik:

4.50t = 100 -3.50t

Det er en første grads ligning for tid, hvis løsning er t = 12.5 s.

b) Begge løperne er i samme posisjon, derfor erstatter den tiden som er oppnådd i forrige seksjon i noen av posisjonslikningene. For eksempel kan vi bruke løperen 1:

x₁ = 4.50t₁ = 56.25 m

Det samme resultatet oppnås ved å erstatte t = 12.5 s i løperens posisjonsligning 2.

-Trening løst 2

Haren utfordrer skilpadden til å løpe en avstand på 2.4 km og for å være rettferdig tilbyr det en halv times fordel. I spillet fremmer skilpadden på grunn 0.25 m/s, som er det maksimale som kan kjøres. Etter 30 minutter løper haren på 2 m/s og når skilpadden raskt.

Etter å ha fortsetter i 15 minutter til, tror han at han har tid til å ta en lur og fortsatt vinne løpet, men sovne i 111 minutter. Når han våkner, løper han med all sin makt, men skilpadden krysset allerede målet. Finne:

a) Hvilken fordel vinner skilpadden?

b) Tidspunktet der haren fremmer skilpadden

c) Øyeblikket som skilpadden går videre til haren.

Løsning på)

Løpet begynner i t = 0. Skilpaddeposisjonen: x_T = 0.25t

Bevegelsen av haren har følgende deler:

Kan tjene deg: Solsystem: planeter, egenskaper, opprinnelse, evolusjon

-Hvile for fordelen det ga til skilpadden: 0 < t < 30 minutos:

-Løp for å nå skilpadden og fortsette å løpe litt etter å ha passert den; Totalt er de 15 minutters bevegelse.

-Sove i 111 minutter (hvile)

-Våkne for sent (Sprint endelig)

2.4 km = 2400 m

Varigheten av løpet var: T = 2400 m/ 0.25 m/s = 9600 s = 160 min. På dette tidspunktet trekker vi 111 minutter fra lur og 30 fordel, som er 19 minutter (1140 sekunder). Det betyr at han løp i 15 minutter før han sov og 4 minutter etter å ha våknet for sprinten.

På dette tidspunktet dekket haren følgende avstand:

d_L = 2 m/s . (femten . 60 s) + 2 m/s (4. 60 s) = 1800 m + 480 m = 2280 m.

Ettersom den totale avstanden var 2400 meter, og trakk begge verdiene, viser det seg at haren manglet 120 meter for å nå målet.

Løsning B)

Hareens plassering før du sovner x_L = 2 (t - 1800), Tatt i betraktning 30 -minutters forsinkelse = 1800 sekunder. Lik x_T og x_L Vi finner tiden de er:

2 (t - 1800) = 0.25t

2t -0.25 t = 3600

T = 2057.14 S = 34.29 min

Løsning C)

Når haren blir avansert av skilpadden, sover som sover 1800 meter fra spillet:

1800 = 0.25t

T = 7200 s = 120 min

applikasjoner

MRU er den enkleste bevegelsen som kan tenkes, og det er derfor den er den første som ble studert i kinematikk, men mange komplekse bevegelser kan beskrives som en kombinasjon av dette og andre enkle bevegelser.

Hvis en person forlater huset sitt og leder til han når en lang rettlinjet motorvei som han reiser til samme hastighet i lang tid, kan bevegelsen hans som MRU beskrives, uten å gå inn på flere detaljer.

Selvfølgelig trenger personen å ta noen få omganger før han går inn og forlater motorveien, men gjennom bruk av denne bevegelsesmodellen kan turens varighet estimeres til å vite omtrentlig avstand mellom utgangspunktet og ankomstpunktet.

I naturen har lyset en jevn rettlinjet bevegelse hvis hastighet er 300.000 km/s. Også bevegelse av lyd i luften kan antas ensartet rettlinjet med hastighet på 340 m/s i en rekke applikasjoner.

Når du analyserer andre problemer, for eksempel bevegelse av lastebærere inne i en førertråd, kan MRU -tilnærmingen også brukes til å gi en ide om hva som skjer i sjåføren.

Referanser

1. Bauer, w. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill.40-45.
2. Figueroa, d. Fysisk serie for vitenskap og ingeniørfag. Volum 3. Utgave. Kinematikk. 69-85.
3. Giancoli, d.  Fysikk: Prinsipper med applikasjoner. 6^th. Ed Prentice Hall. 19-36.
4. Hewitt, Paul. 2012. Konseptuell fysisk vitenskap. 5^th. Ed. Pearson. 14-18.
5. Kirkpatrick, l. 2007. Fysikk: En titt på verden. 6^ta Forkortet utgave. Cengage Learning. 15-19.
6. Wilson, J. 2011. Fysikk 10. Pearson Education. 116-119.