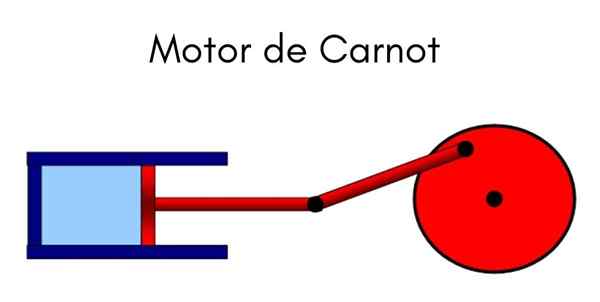
Carnot Machine

Hva er Carnot -maskinen?

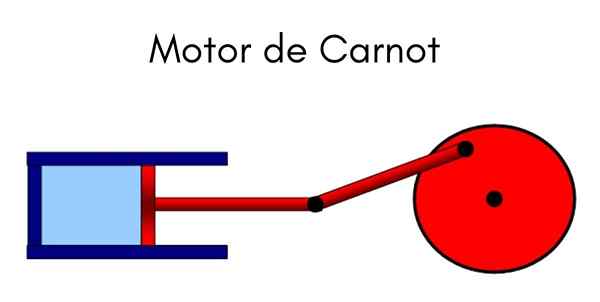
De Carnot Machine Det er en ideell syklisk modell der varme brukes til å gjøre en jobb. Systemet kan forstås som et stempel som beveger seg inne i en sylinder som komprimerer en gass. Syklusen som utøves er den fra Carnot, uttalt av faren til termodynamikk, den franske fysikeren og ingeniøren Nicolas Leonard Sadi Carnot.

Carnot uttalte denne syklusen på begynnelsen av det nittende århundre. Maskinen er utsatt for fire tilstandsvariasjoner, vekslende forhold som konstant temperatur og trykk, der det er bevist en variant av volumet når du komprimerer og utvider gass.

Formler

I følge Carnot er det mulig å maksimere ytelsen som er oppnådd den ideelle maskinen for temperatur og trykkvariasjoner.

Carnot -syklusen må analyseres separat i hver av sine fire faser: isotermisk ekspansjon, adiabatisk ekspansjon, isotermisk kompresjon og adiabatisk kompresjon.

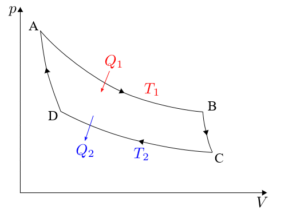
Formlene tilknyttet hver av fasene i syklusen som utøves på Carnot -maskinen vil bli detaljert nedenfor.

Isotermisk ekspansjon (A → B)

Lokalene for denne fasen er følgende:

• Gassvolum: Det går fra minimumsvolumet til et gjennomsnittlig volum.
• Maskintemperatur: Konstant temperatur T1, høy verdi (T1> T2).
• Maskintrykk: Ned fra P1 til P2.

Den isotermiske prosessen innebærer at temperatur T1 ikke varierer i denne fasen. Varmeoverføring induserer gassutvidelse, noe som induserer bevegelse på stempelet og produserer mekanisk arbeid.

Når man utvides, presenterer gassen en viss tendens til å avkjøle. Imidlertid absorberer den varmen som sendes ut av temperaturkilden, og under utvidelsen opprettholder den den konstante temperaturen.

Kan tjene deg: Hva er den lineære hastigheten? (Med løste øvelser)

Siden temperaturen forblir konstant under denne prosessen, endres ikke den indre energien til gassen, og all varmen som absorberes av gassen blir effektivt transformert til arbeid. Så:

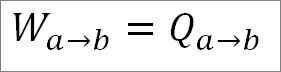
På den annen side, på slutten av denne fasen av syklusen er det også mulig å oppnå trykkverdien ved å bruke den ideelle gassligningen for den. På denne måten har du følgende:

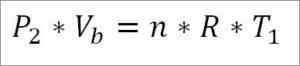
I dette uttrykket:

• P₂: Trykk på slutten av fasen.
• V_b: Volum på punkt B.
• N: Antall mol gass.
• A: Universell konstant av ideelle gasser. R = 0,082 (atm*liter)/(mol*k).
• T1: Absolutt starttemperatur, Kelvin grader.

Adiabatisk ekspansjon (B → C)

I løpet av denne fasen av prosessen utføres gassutvidelse uten behov for å bytte varme. På denne måten er lokalene detaljert nedenfor:

• Gassvolum: Det går fra gjennomsnittlig volum til et maksimalt volum.
• Maskintemperatur: Ned fra T1 til T2.
• Maskintrykk: konstant P2 -trykk.

Den adiabatiske prosessen innebærer at P2 -trykket ikke varierer i denne fasen. Temperaturen avtar og gassen fortsetter å utvide seg til den når maksimalt volumet; det vil si at stempelet når toppen.

I dette tilfellet kommer arbeidet som er utført fra den interne energien til gassen og dets verdi er negativt fordi energi avtar under denne prosessen.

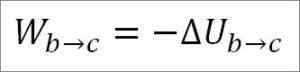
Forutsatt at det er en ideell gass, opprettholdes teorien at gassmolekyler bare har kinetisk energi. I henhold til termodynamikkprinsippene kan dette trekkes ut av følgende formel:

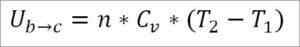
I denne formelen:

• ∆U_{B → c}: Intern energivariasjon av den ideelle gassen mellom punktene B og C.
• N: Antall mol gass.
• CV: Gass molar varmekapasitet.
• T1: Absolutt starttemperatur, Kelvin grader.
• T2: Absolutt slutttemperatur, Kelvin grader.

Kan tjene deg: Isobarisk prosess: Formler, ligninger, eksperimenter, øvelser

Isotermisk komprimering (C → D)

I denne fasen begynner komprimeringen av gass; det vil si at stempelet mobiliseres i sylinderen, som gassen trekker seg sammen med volumet.

Forholdene som ligger i denne prosessen er detaljert nedenfor:

• Gassvolum: Det går fra det maksimale volumet til et mellomvolum.
• Maskintemperatur: konstant temperatur T2, redusert verdi (T2 < T1).
• Maskintrykk: Øk fra P2 til P1.

Her øker trykket på gassen, så det begynner å komprimere. Imidlertid forblir temperaturen konstant, og derfor er den indre energisiasjonen til gassen null.

Analog til den isotermiske ekspansjonen, det utførte arbeidet er lik varmen i systemet. Så:

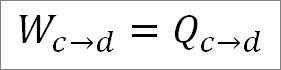
Det er også mulig å finne presset på dette tidspunktet ved å bruke den ideelle gassligningen.

Adiabatisk komprimering (D → A)

Dette er den siste fasen av prosessen, der systemet går tilbake til sine opprinnelige forhold. For å gjøre dette vurderes følgende forhold:

• Gassvolum: Det går fra et mellomvolum til et minimumsvolum.
• Maskintemperatur: Øk fra T2 til T1.
• Maskintrykk: konstant trykk P1.

Varmekilden som er innlemmet i systemet i forrige fase blir fjernet, slik at den ideelle gassen vil øke temperaturen i mellomtiden trykket forblir konstant.

Gassen går tilbake til de opprinnelige temperaturforholdene (T1) og ved volumet (minimum). Nok en gang kommer arbeidet som er gjort fra den interne energien til gassen, så du må:

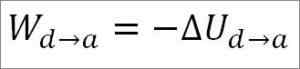
I likhet med tilfellet med adiabatisk ekspansjon, er det mulig å oppnå variasjonen av gassenergi gjennom følgende matematiske uttrykk:

Kan tjene deg: kalsiumfluor (CAF2): Struktur, egenskaper, bruk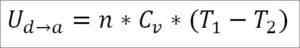

Hvordan fungerer Carnot -maskinen?

Carnot -maskinen fungerer som en motor der ytelsen maksimeres av variasjon av isotermiske og adiabatiske prosesser, veksler faser av utvidelse og forståelse av en ideell gass.

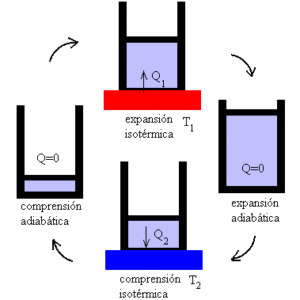
Mekanismen kan forstås som et ideelt apparat som utøver en jobb som blir utsatt for varmevariasjoner, gitt eksistensen av to temperaturspotelys.

I det første fokuset blir systemet utsatt for en T1 -temperatur. Det er en høy temperatur som legger systemet for å stresse og produserer gassutvidelse.

På sin side oversettes dette til utførelsen av et mekanisk verk som tillater mobilisering av stempelet ut av sylinderen, og hvis grense bare er mulig ved adiabatisk ekspansjon.

Så kommer det andre fokuset, der systemet blir utsatt for en T2 -temperatur, mindre enn T1; det vil si at mekanismen er underlagt avkjøling.

Dette induserer varmeutvinning og gass knusing, som når dets første volum etter adiabatisk komprimering.

applikasjoner

Carnot -maskinen har blitt mye brukt takket være sitt bidrag i forståelsen av de viktigste aspektene ved termodynamikk.

Denne modellen lar deg tydelig forstå variasjonene til ideelle gasser som er utsatt for temperatur- og trykkendringer, som er en referansemetode når du utformer ekte motorer.