Ungarsk metode som består av eksempel

Han Ungarsk metode Det er en algoritme som brukes i tildelingsproblemer når du vil minimere kostnadene. Det vil si at det brukes til å finne minimumskostnadene ved å tildele flere personer til forskjellige aktiviteter basert på lavest kostnad. Hver aktivitet må tilordnes en annen person.

Et oppdragsproblem er en spesiell type lineært programmeringsproblem, der målet er å minimere kostnadene eller tiden for å fullføre en mengde arbeid av flere mennesker.

Kilde: Pixabay.com

Et av de viktige egenskapene ved tildelingsproblemet er at bare ett arbeid (eller arbeider) er tildelt en maskin (eller prosjekt).

Denne metoden ble utviklet av den ungarske matematikeren D. Konig. Av denne grunn er det kjent som den ungarske metoden for tildelingsproblemer. Det er også kjent som Kuhn-Munkres Assignment Algorithm.

Ethvert tildelingsproblem kan løses enkelt ved å bruke denne metoden som består av to faser:

- Med den første fasen er det reduksjoner av rader og kolonneduksjoner.

- I den andre fasen er løsningen på en iterativ base optimalisert.

[TOC]

Hva er den ungarske metoden?

Den ungarske metoden består av fire trinn. De to første trinnene utføres bare en gang, mens trinn 3 og 4 gjentas til de finner en optimal oppgave.

Det regnes som inngangsfakta til en firkantet matrise av orden n av n, som bare må inneholde ikke -negative elementer.

For et gitt problem, hvis antall rader i matrisen ikke er lik antall kolonner, må en fiktiv rad eller en fiktiv kolonne legges til, avhengig av saken. Tildelingskostnader for disse fiktive cellene er alltid tildelt som null.

Trinn 1: Trekk minimum på hver rad

For hver rad i matrisen er elementet valgt med lavest verdi og subtraksjoner av hvert element i den raden.

Kan tjene deg: Hva er den nåværende eiendelen? (Med eksempler)

Trinn 2: Trekk minimum på hver kolonne

Tilsvarende velges elementet med den laveste verdien for hver kolonne og trekker det fra hvert element i den kolonnen.

Trinn 3: Dekk alle nuller med et minimum antall linjer

Alle nuller må dekkes i matrisen som følge av trinn 2 ved å bruke et minimum antall horisontale og vertikale linjer, enten med rader eller kolonner.

Hvis det er nødvendig.

Ellers, hvis det kreves mindre linjer for å dekke alle nuller i matrisen, fortsetter det med trinn 4.

Trinn 4: Lag flere nuller

Det minste elementet i matrisen (kalt k) er valgt som ikke er dekket av en av linjene laget i trinn 3.

Verdien av K for alle elementer som ikke er dekket av linjer, trekkes fra. Deretter blir verdien av k lagt til alle elementene som er dekket av skjæringspunktet mellom to linjer.

Elementene som er dekket av en enkelt linje blir igjen som de er. Etter å ha utført dette trinnet, går du tilbake til trinn 3.

Optimal tildeling

Når algoritmen er stoppet i trinn 3, blir et sett med nuller valgt slik at hver rad og hver kolonne bare har en valgt null.

Hvis det i denne utvelgelsesprosessen ikke er noen null på rad eller kolonne, vil en av disse nuller bli valgt. De resterende nuller blir eliminert i den kolonnen eller raden, og gjentar det samme for de andre oppgavene også.

Det kan tjene deg: makrolokalisering

Hvis det ikke er en enkelt tildeling av nuller, betyr det at det er flere løsninger. Kostnadene vil imidlertid forbli de samme for de forskjellige tildelingssettene.

Enhver fiktiv rad eller kolonne som er lagt til, blir eliminert. Zeros valgt i denne endelige matrisen tilsvarer den ideelle oppgaven som kreves i den opprinnelige matrisen.

Eksempel

Tenk på et selskap der det er fire aktiviteter (A1, A2, A3, A4) som må utføres av fire arbeidere (T1, T2, T3, T4). En aktivitet per arbeider må tilordnes.

Følgende matrise viser kostnadene for å tildele en viss arbeider til en viss aktivitet. Målet som følges er å minimere den totale kostnaden for oppgaven som sammensatte av disse fire aktivitetene.

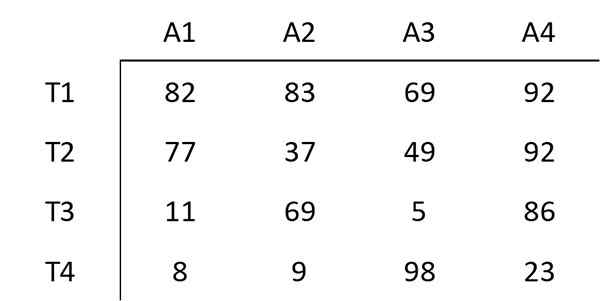
Trinn 1: Trekk minimum på hver rad

Elementet begynner med minimumsverdien for hver rad av de andre elementene i den raden. For eksempel er det minste elementet i første rad 69. Derfor trekkes 69 av hvert element i første rad. Den resulterende matrisen er:

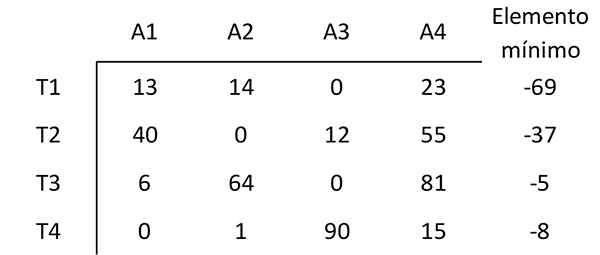
Trinn 2: Trekk minimum på hver kolonne

På samme måte blir elementet trukket fra med minimumsverdien for hver kolonne i de andre elementene i den kolonnen, og oppnår følgende matrise:

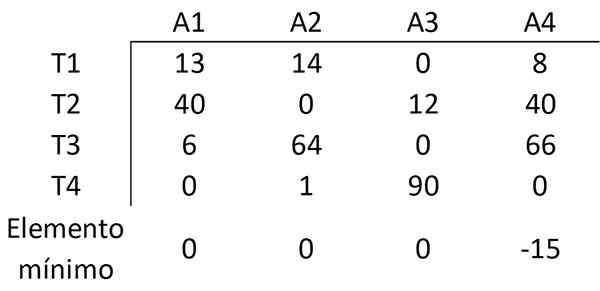
Trinn 3: Dekk alle nuller med et minimum antall linjer

Nå vil minimum antall linjer (horisontalt eller vertikalt) bli bestemt som kreves for å dekke alle nuller i matrisen. Alle nuller kan dekkes med 3 linjer:

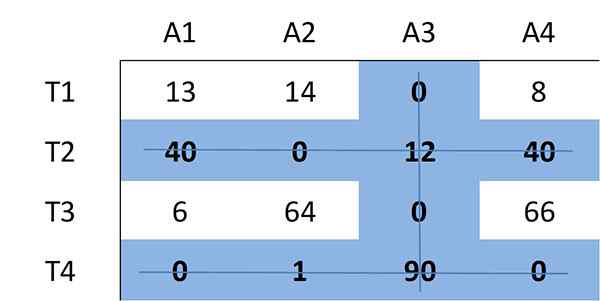
Fordi antall nødvendige linjer er tre og er mindre enn størrelsen på matrisen (n = 4), fortsetter det med trinn 4.

Kan tjene deg: Prosjektledelse: Hva er, faser, mål, eksempler

Trinn 4: Lag flere nuller

Det laveste elementet som ikke er dekket av linjene er valgt, hvis verdi er 6. Denne verdien av alle ikke -dekkede elementer blir trukket fra, og den samme verdien legges til alle elementene som dekkes av skjæringspunktet mellom to linjer. Dette resulterer i følgende matrise:

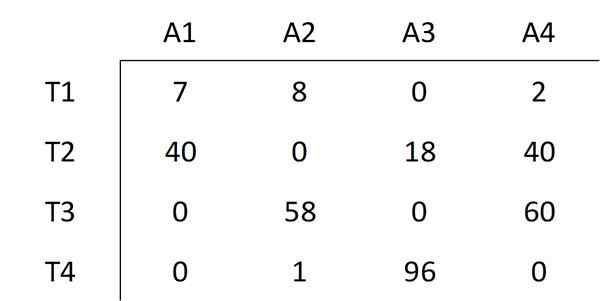
Som antydet i den ungarske metoden, må trinn nummer tre gjennomføres igjen.

Trinn 3 (repetisjon)

Igjen er minimum antall linjer som kreves for å dekke alle nuller i matrisen bestemt. Denne gangen er det nødvendig med fire linjer:

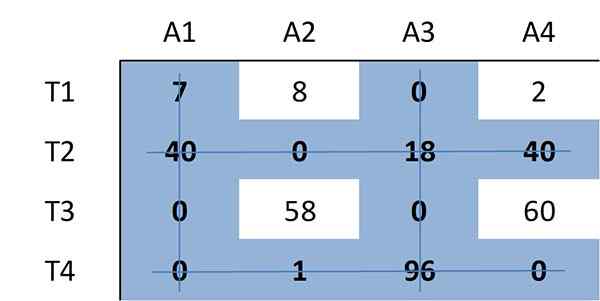
Fordi antallet linjer som kreves er 4, lik størrelsen på matrisen (n = 4), er det en optimal oppgave mellom nuller i matrisen. Derfor stopper algoritmen.

Optimal tildeling

Som indikert med metoden, tilsvarer utvalget av følgende nuller en optimal oppgave:

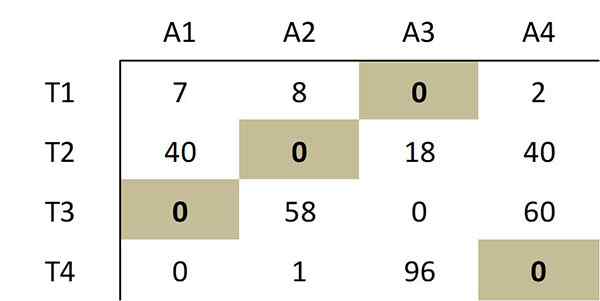
Dette utvalget av nuller tilsvarer følgende optimale tildeling i den opprinnelige kostnadsmatrisen:

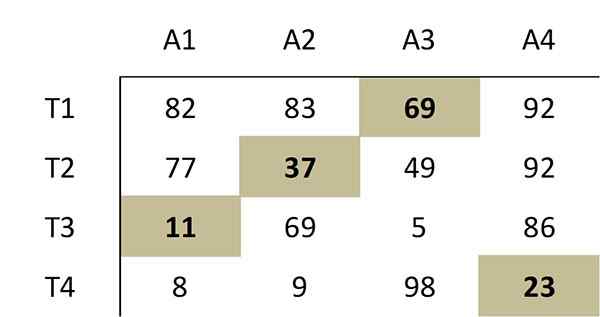
Derfor må arbeideren 1 utføre aktivitet 3, arbeideren 2, aktiviteten 2, arbeideren 3, aktiviteten 1 og arbeideren 4 må utføre aktiviteten 4. Den totale kostnaden for denne optimale tildelingen er 69+37+11+23 = 140.

Referanser

1. Ungarn Algoritme (2019). Ungarn -algoritmen. Hentet fra: Hungarianalgoritme.com.
2. Studie (2019). Bruke Ungarn -algoritmen for å løse oppdragsproblemer. Hentet fra: studie.com.
3. Wisdom Jobs (2018). Ungarn -metode for å løse tildelingsproblem - Kvantitative teknikker for styring. Hentet fra: Wisdomjobs.com.
4. Geeks for geeks (2019). Ungary -algoritme for tildelingsproblem. Hentet fra: geeksforgeeks.org.
5. Karleight Moore, Nathan Landman (2019). Ungarn maksimal matchende algoritme. Strålende. Hentet fra: strålende.org.