Tilfeldig prøvetakingsmetodikk, fordeler, ulemper, eksempler

Han Tilfeldig prøvetaking Det er måten å velge et statistisk representativt utvalg fra en gitt befolkning. En del av prinsippet om at hvert element i prøven må ha samme sannsynlighet for å bli valgt.

En tombola er et eksempel på tilfeldig prøvetaking, der hvert medlem av befolkningen av deltakerne tildeles et tall. For å velge tallene som tilsvarer tombolaprisene (prøven) brukes noen tilfeldige teknikker, for eksempel utdrag fra en postkasse tallene som ble scoret på identiske kort.

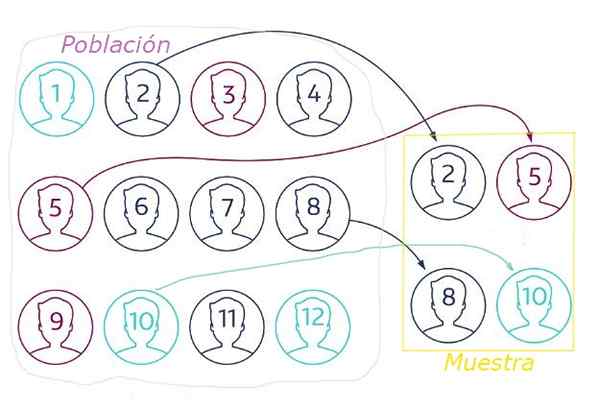Figur 1. I tilfeldig prøvetaking blir prøven trukket ut fra tilfeldig populasjon gjennom en viss teknikk som sikrer at alle elementer har samme sannsynlighet for å bli valgt. Kilde: NetQuest.com.

I tilfeldig prøvetaking er det viktig.

[TOC]

Størrelsen på prøven

Det er formler for å bestemme riktig størrelse på en prøve. Den viktigste faktoren å vurdere er om befolkningsstørrelsen er kjent eller ikke. La oss se på formlene for å bestemme prøvestørrelsen:

Sak 1: Befolkningsstørrelse er ikke kjent

Når befolkningens størrelse er ukjent, er det mulig å velge en adekvat N -prøve, for å avgjøre om en viss hypotese er sann eller falsk.

For dette brukes følgende formel:

n = (z² P q)/(e²)

Hvor:

-P Det er sannsynligheten for at hypotesen er sann.

-Q er sannsynligheten for at det ikke er, derfor q = 1 - P.

-E er den relative feilmarginen, for eksempel har en 5% feil en margin E = 0,05. 

-Z har å gjøre med det selvtillitsnivået som kreves av studien.

Kan tjene deg: Normal distribusjon: Formel, egenskaper, eksempel, trening

I en normalfordeling karakterisert (eller normalisert) har et 90% konfidensnivå z = 1.645, fordi sannsynligheten for at resultatet er mellom -1.645σ og +1.645σ er 90%, der σ er standardavviket.

Tillitsnivåer og deres tilsvarende z -verdier 

1.- 50% konfidensnivå tilsvarer z = 0,675.

2.- 68.3% konfidensnivå tilsvarer z = 1.

3.- 90% konfidensnivå tilsvarer z = 1.645.

4.- 95% konfidensnivå tilsvarer z = 1,96

5.- 95,5% konfidensnivå tilsvarer z = 2.

6.- 99,7% konfidensnivå tilsvarer z = 3.

Et eksempel der denne formelen kan brukes, vil være i en studie for å bestemme gjennomsnittsvekten til småsteinene på en strand.

Det er klart det ikke er mulig å studere og veie alle småsteinene på stranden, så det er praktisk.

Figur 2. For å studere egenskapene til småsteinene på en strand er det nødvendig å velge en tilfeldig prøve med et representativt antall av dem. (Kilde: Pixabay)

Sak 2: Befolkningsstørrelse er kjent

Når antallet n elementer som utgjør en viss populasjon (eller univers) er kjent, hvis du vil velge ved enkel tilfeldig prøvetaking av en statistisk signifikant prøveprøve, er dette formelen: 

n = (z²p q n)/(n e² + Z²P Q)

Hvor:

-Z er koeffisienten forbundet med tillitsnivået.

-P er sannsynligheten for suksess med hypotesen.

-Q er sannsynligheten for svikt i hypotesen, P + Q = 1.

-N er størrelsen på den totale befolkningen.

-E er den relative feilen i studieresultatet.

Eksempler

Metodikken for å trekke ut prøvene avhenger mye av den typen studier som kreves for å gjøre. Derfor har tilfeldig prøvetaking utallige applikasjoner:

Kan tjene deg: tegn på gruppering

Undersøkelser og spørreskjemaer

For eksempel i telefonundersøkelser blir folk valgt til å bli konsultert av en tilfeldig tallgenerator, som gjelder for regionen som studeres.

Hvis du vil bruke et spørreskjema på de ansatte i et stort selskap, kan utvalget av respondenter brukes gjennom deres ansattnummer, eller identitetskortnummer.

Dette nummeret må også velges tilfeldig ved å bruke en tilfeldig tallgenerator for eksempel.

Figur 3. Et spørreskjema kan brukes tilfeldig å velge deltakere. Kilde: Pixabay.

QA

I tilfelle studien er på delene produsert av en maskin, må deler velges tilfeldig, men av partier laget til forskjellige tider av døgnet, eller i forskjellige dager eller uker.

Fordeler

Enkel tilfeldig prøvetaking:

- Det gjør det mulig å redusere kostnadene ved en statistisk studie, fordi det ikke er nødvendig å studere den totale populasjonen for å oppnå statistisk pålitelige resultater, med ønsket tillitsnivå og feilnivået som kreves i studien.

- Unngå skjevhet: Ettersom valget av elementene som skal studeres er helt tilfeldig, gjenspeiler studien trofast egenskapene til befolkningen, selv om bare en del av det samme ble studert.

Ulemper

- Metoden er ikke tilstrekkelig i tilfeller du vil vite preferansene i forskjellige grupper eller befolkningsstrata.

I dette tilfellet er det å foretrekke å tidligere bestemme gruppene eller segmentene som studien er gjort. Når lagene eller gruppene er definert, så hvis det er praktisk for hver av dem å bruke tilfeldig prøvetaking.

- Det er veldig usannsynlig at informasjon om minoritetssektorene er oppnådd, hvorav det noen ganger er nødvendig å kjenne deres egenskaper.

Kan tjene deg: Simpson Rule: Formel, demonstrasjon, eksempler, øvelser

For eksempel, hvis det er en kampanje på et dyrt produkt, er det nødvendig å kjenne preferansene til de rikeste minoritetssektorene.

Trening løst

Vi ønsker å studere befolkningens preferanse forresten Cola of Cola, men det er ingen tidligere studier i den befolkningen, hvorav den er ukjent.

På den annen side må utvalget være representativt med et minimum konfidensnivå på 90%, og konklusjonene må ha en prosentvis feil på 2%.

-Hvordan bestemme S -størrelsen på prøven?

-Hva ville være prøvestørrelsen hvis feilmarginen er gjort opp til 5%?

Løsning

Siden populasjonsstørrelsen er ukjent, for å bestemme størrelsen på prøven, brukes formelen som er gitt ovenfor:

n = (z²P q)/(e²)

Vi antar at det er samme sannsynlighet for preferanse (p) ved vår forfriskning av ikke -preferanse (q), deretter p = q = 0,5.

På den annen side, ettersom studieresultatet må ha en prosentvis feil mindre enn 2%, vil den relative feilen være 0,02.

Til slutt produserer en verdi z = 1.645 et 90% konfidensnivå.

Kort sagt, du har følgende verdier:

Z = 1.645

P = 0,5

Q = 0,5

E = 0,02

Med disse dataene beregnes minimumsprøvestørrelsen:

N = (1.645² 0,5 0,5)/(0,02²) = 1691.3

Dette betyr at studien med feilmarginen som kreves og med valgt tillitsnivå, må ha et utvalg av respondenter av minst 1692 individer, valgt ved enkel tilfeldig prøvetaking.

Hvis du går fra en feilmargin fra 2% til 5%, er den nye prøvestørrelsen:

N = (1.645² 0,5 0,5)/(0,05²) = 271

Som er et betydelig lavere antall individer. Avslutningsvis er prøvestørrelsen veldig følsom for ønsket margin i studien.

Referanser

1. Berenson, m. 1985.Statistikk for administrasjon og økonomi, konsepter og applikasjoner. Inter -amerikansk redaksjon.
2. Statistikk. Tilfeldig prøvetaking. Hentet fra: Encyclopediaeconomica.com.
3. Statistikk. Prøvetaking. Gjenopprettet fra: Statistikk.Matte.Uson.MX.
4. Utforskelig. Tilfeldig prøvetaking. Gjenopprettet fra: utforskbar.com.
5. Moore, d. 2005. Grunnleggende statistikk anvendt. 2. Utgave.
6. NetQuest. Tilfeldig prøvetaking. Gjenopprettet fra: NetQuest.com.
7. Wikipedia. Statistisk prøve. Hentet fra: i.Wikipedia.org