Motsatte vinkler av toppunktet (med en løst øvelse)

De Motsatte vinkler av toppunktet De er de som oppfyller følgende: sidene av en av dem er forlengelsene på sidene av den andre vinkelen. Han Grunnleggende teorem Av de motsatte vinklene ved toppunktet står det: to vinkler motarbeidet av toppunktet har samme tiltak.

Mange ganger blir språket misbrukt ved å si at vinklene motarbeidet av toppunktet er de samme, noe som ikke er riktig. Det faktum at to vinkler har samme tiltak, betyr ikke at de er like. Det er som å si at to barn som har samme høyde er like.

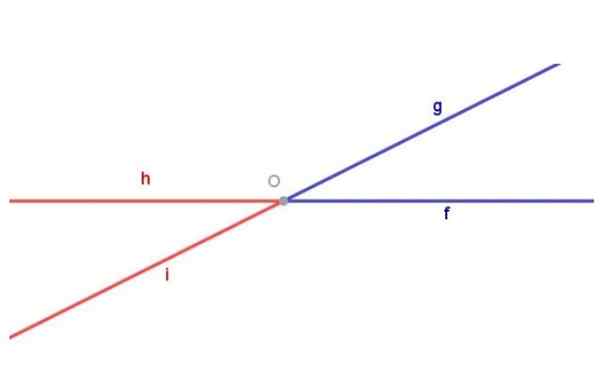
Figur 1. Motsatte vinkler av toppunktet. Utarbeidet av: Fanny Zapata.

Husk at en vinkel er definert som den geometriske figuren sammensatt av to semi -rett med samme opprinnelse.

Figur 1 viser vinkelen TÅKE (Blå) sammensatt av semi -rekreasjon [Av) og semi -Straight [OG) av vanlig opprinnelse ENTEN. Figur 1 viser også vinkelen Hoi (rød) sammensatt av semi -recreational [Jeg hørte) og semi -Straight [ÅH) begge med opprinnelse ENTEN. 

To motsatte vinkler med toppunktet er to forskjellige geometriske figurer. For å fremheve dette, i figur 1 har vinkelen farget TÅKE Blå, mens vinkelen Hoi Han har farget rødt. 

De blå og røde vinklene i figur 1 er motarbeidet av toppunktet fordi: semi -rettigheten [Av) av den blå vinkelen er forlengelsen av semi -rettigheten [ÅH) av den røde vinkelen og semi -rettigheten [OG) av den blå vinkelen er forlengelsen av semi -rettigheten [Jeg hørte) av den røde vinkelen.

[TOC]

Viktige konsepter om vinkler

Sider og hjørner i en vinkel

Den geometriske figuren bestående av to semi -straks med vanlig opprinnelse er en vinkel. Følgende bilde viser vinkelen Poq dannet av de to semi -rettighetene [OP) og [OQ) av vanlig opprinnelse ENTEN:

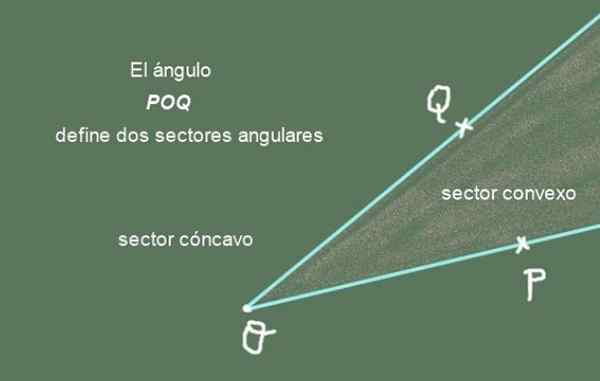Figur 2. POQ -vinkelen definerer to kantete sektorer. Utarbeidet av: f. Zapata.

Semi -Straight [OP) og [OQ) er sider av vinkelen Poq, mens felles punktet eller kalles Vértice av vinkelen.

Kan tjene deg: Sturges -regel

Vinkel sektor: En vinkel deler flyet som inneholder det i to kantete sektorer. Den ene av dem er den konvekse vinkelsektoren og den andre er den konkave kantete sektoren. Foreningen av de to sektorene gir hele flyet.

Figur 2 viser i vinkelen Poq og dens to kantete sektorer. Den konvekse kantete sektoren er den som har en spiss form, mens den konkave er vinkelsektoren i flyet som mangler den konvekse sektoren.

Vinkler dannet av to linjer som er kuttet

To linjer i et plan som er avskjært fra fire vinkler og deler planet i fire kantete sektorer.

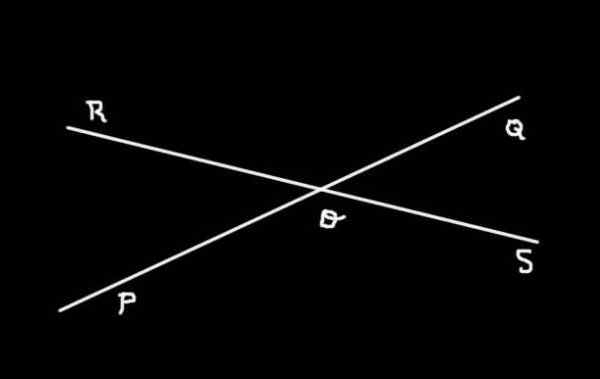Figur 3. Linjene (PQ) og (Rs) blir oppfanget i O og form 4 vinkler. Utarbeidet av: f. Zapata.

Figur 3 viser de to linjene (PQ) og (Rs) avskjært i ENTEN. Der kan du se at fire vinkler er bestemt:

-SOQ, Qor, Rop og Pos

Vinklene SOQ og Qor, Qor og ROP, ROP og Pos, Pos og SOQ er  tilstøtende vinkler mellom seg selv, mens SOQ og Rop De er motarbeidet av toppunktet. De er også Motsatte vinkler av toppunktet Vinklene Qor og Pos.

Vinkelrett linjer og rett vinkel

To tørkelinjer (rette linjer krysser hverandre) er Vinkelrett rette linjer Hvis de bestemmer fire vinkel sektorer med like mål. Hvis hver av de fire sektorene er symmetriske med den tilstøtende vinkelsektoren, har de samme tiltak.

Hver av vinklene som bestemmer de to vinkelrette linjene kalles rett vinkel. Alle rette vinkler har samme mål.

Semi -straks på samme linje og flat vinkel

Gitt en linje og et poeng av det, er to semi -straks definert. De to semi -strakede definerer to flate vinkler.

I figur 3 kan linjen observeres (Rs) Og poenget ENTEN som tilhører (Rs). Vinkelen Sor Det er en flat vinkel. Det kan også bekreftes at vinkelen Ros Det er en flat vinkel. Alle flate vinkler har samme mål.

Kan tjene deg: Clausurative eiendom

Nullvinkel og full vinkel

En enkelt semi -recreational definerer to vinkler: en av dem i den konvekse kantete sektoren er Nullvinkel Og den andre, den av den konkave kantete sektoren er full vinkel. I figur 3 Nullvinkel Sos og full vinkel Sos. 

Mål 

Det er to numeriske systemer som ofte brukes til å gi måling av en vinkel. 

En av dem er det sexagesimale systemet, det vil si basert på nummer 60. Det er en arv fra de gamle mesopotamiske kulturene. Det andre vinklet målesystemet er Radián -systemet, basert på antall π (PI) og er en arv fra de gamle greske vismennene som utviklet geometri.

Sexagesimal system

Nullvinkel: I det sexagesimale systemet måler nullvinkelen 0º (null grader).

Full vinkel: 360º -tiltaket er tildelt (tre hundre og seksti grader).

Flat vinkel: I det sexagesimale systemet måler flatvinkelen 180º (hundre åtti grader).

Rett vinkel: To vinkelrett linjer deler planet i fire vinkler med like mål kalt rette vinkler. Målet på en rett vinkel er en fjerdedel av full vinkel, det vil si nitti grader).

Transportør eller goniometer

Transportøren er instrumentet som brukes til å måle vinkler. Den består av en halvsirkel (vanligvis gjennomsiktig plast) delt inn i 180 vinkel seksjoner. Når en halvsirkel danner en flat vinkel, er målet mellom to påfølgende seksjoner 1.

Goniometeret ligner på transportøren og består av en sirkel delt inn i 360 vinkelseksjoner.

En vinkel hvis sider starter fra midten av goniometeret avskjærer to sektorer og målet på den vinkelen i grader er lik antallet n av seksjoner mellom de to avskjærte sektorene, i dette tilfellet vil tiltaket være nr. (Lyder ““ENE grader).

Det kan tjene deg: Square centimeter til kvadratmeter (cm² til m²)

Teorem om de motsatte vinklene ved toppunktet

Formelt sett er teoremet oppgitt på denne måten:

Hvis to vinkler er imot toppunktet, har de samme tiltak.

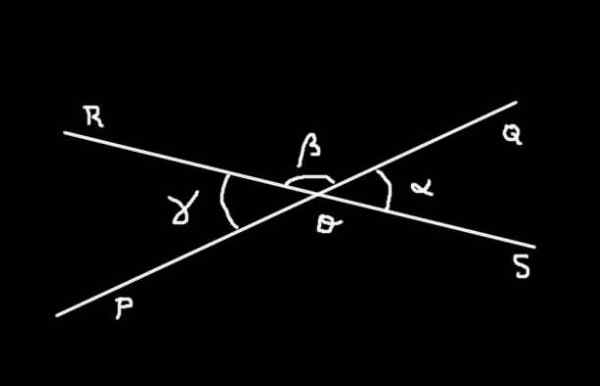Figur 4. α, β og γ er målene for SOQ-, QOR- og ROP -vinklene. Utarbeidet av: f. Zapata.

Demonstrasjon

Vinkelen SOQ Det har α -mål; vinkelen Qor Det har β -mål og vinkelen Rop Den har y -mål. Summen av vinkelen SOQ mer ham Qor danner den flate vinkelen Sor av tiltak 180º.

Det er:

α + β = 180º

På den annen side og bruker samme resonnement med vinklene Qor og Rop Du har:

β + γ = 180º

Hvis vi observerer de to foregående ligningene, er den eneste måten begge er oppfylt på at α er lik γ.

Som SOQ Den har α -mål og er motarbeidet av toppunktet til Rop av mål γ, og som α = γ, konkluderes det med at vinklene motarbeidet av toppunktet har samme mål.

Trening løst

Med henvisning til figur 4: Anta at β = 2 α. Finn målet på vinklene SOQ, Qor og Rop I sexagesimale grader.

Løsning

Som summen av vinkelen SOQ mer ham Qor danner den flate vinkelen Sor Du har:

α + β = 180º

Men de forteller oss at β = 2 α. Erstatte denne verdien av β vi forblir:

α + 2 α = 180º

Det er å si:

3 α = 180º

Noe som betyr at α er den tredje delen av 180º:

α = (180º / 3) = 60º

Deretter målet på SOQ er α = 60º. Målet på Qor er β = 2 α = 2*60º = 120º. Endelig som Rop er motarbeidet av toppunktet til SOQ I henhold til teoremet demonstrerte allerede at de har samme tiltak. Det vil si målet på Rop er γ = α = 60º. 

Referanser

1. Baldor, J. TIL. 1973.Flat og romgeometri. Sentralamerikansk kulturell. 
2. Matematiske lover og formler. Vinkelmålingssystemer. Hentet fra: Ingemecanica.com.
3. Wikipedia. Motsatte vinkler av toppunktet. Gjenopprettet fra: er.Wikipedia.com
4. Wikipedia. Transportør. Gjenopprettet fra: er.Wikipedia.com
5. Zapata f. Goniometer: historie, deler, drift. Hentet fra: Lifer.com