Matte

Vinkler og trekanter

Vinkler og trekanter
Vinklene og trekantene er en del av flat geometri. Shuttersock

Hva er vinkler og trekanter?

EN vinkel Det er regionen av flyet avgrenset av to semi -straks med et opprinnelsessted i felles. Dette punktet er kjent som toppunkt, Mens semi -strak kalles sider. På den annen side, en triangel Det er en figur av tre vinkler og tre sider, med tre hjørner.

Vi vil snakke om vinklene først.

Vinkler

Det er flere måter å betegne vinklene: gjennom greske bokstaver som α, β, γ, som en circumflex -aksent kan tilsettes; med store bokstaver polstret eller små bokstaver, a, b, c, a, b, c; Tall, for eksempel 1, 2, 3 ... eller bruk av vinkelsymbolet ∠.

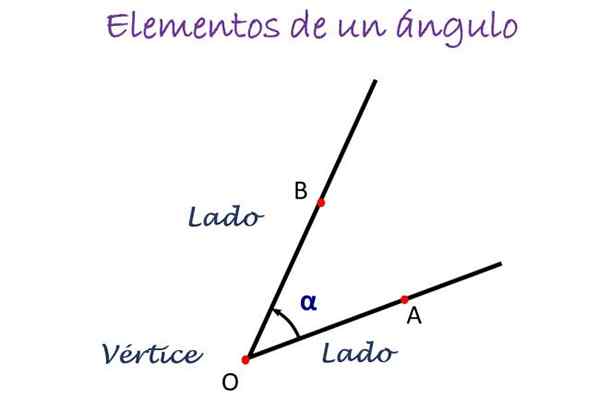Hovedelementene i en vinkel. Kilde: f. Zapata

I figuren over måles vinkelen fra side A til B, indikert med pilens retning, og i sentrum er bokstaven som betegner toppunktet plassert, som normalt er eller. Vinkelen blir deretter betegnet som ∠ AOB.

Når vinkelen måles i en antihorarium forstand, tildeles A +-tegn vilkårlig, og hvis det måles i en plan, et tegn -for å skille dem.

Målet på vinklene utføres ved hjelp av en transportør, som består av et halvsirkulært plastark som den som er vist nedenfor. Halvsirkelen er delt inn i 180 like deler, hver samtale grad.

For å måle, er toppunktet av vinkelen sammenfalt med transportørens sentrale punkt, indikert med pilen, og den første siden med en av kantene, indre eller eksterne. Den endelige siden krysser noen av transportørens merker, dette tiltaket er vinkelen.

Kan tjene deg: Empirisk regel: Hvordan bruke det, hva er det for, løste øvelser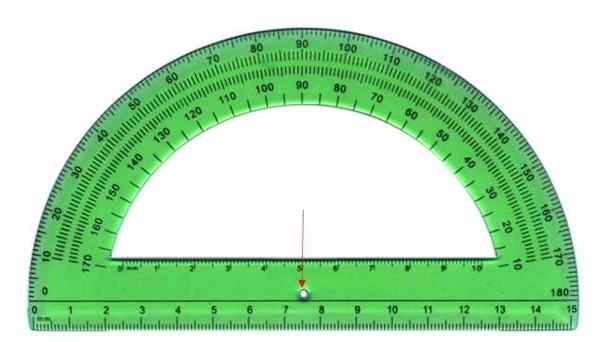Transportøren er instrumentet for å måle vinkler. Kilde: Wikimedia Commons

Typer vinkler

Et av de mest brukte kriteriene for å klassifisere vinkler, er i henhold til dets mål. Derfor kan en vinkel være:

  • Null, Tiltak 0º.
  • Skarp, hvis tiltak er mellom 0 og 90º.
  • Rett, Den måler nøyaktig 90º.
  • Stump, Den er større enn 90 º og mindre enn 180º.
  • Flat, Tiltaket er lik 180º.
  • Fullstendig, representerer en fullstendig sving og måler 360º.
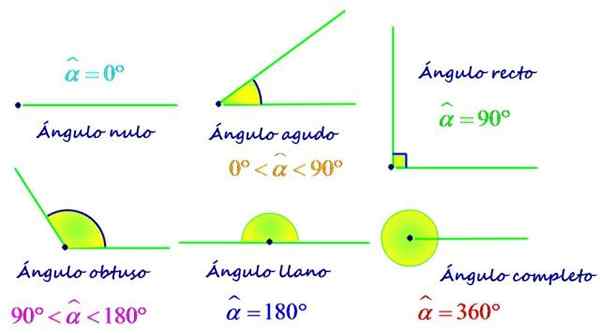Typer vinkler i henhold til ditt mål. Kilde: f. Zapata.

I henhold til forholdet mellom dens mål og det i den flate vinkelen, som er 180º, kan vinklene også klassifiseres som:

  • Konkav, Hvis den måler mindre enn 180º. Derfor er de akutte, rette og stumpe vinklene konkave, siden dets mål alltid er mindre enn 180 º (se figuren over).
  • Konveks, Hvis tiltaket ditt er større enn 180º, som vinklene på 270 º og 360º.

Vinkler i henhold til summen av deres tiltak og i henhold til sidens plassering

To vinkler ∠ A og ∠ B kan være:

  • Komplementær, Hvis summen av tiltakene er lik 90º.
  • Tillegg, Når du legger til de respektive tiltakene, oppnås 180º.
  • Konjugert, Hvis denne summen er lik 360º.
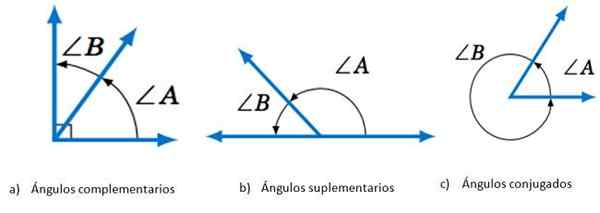Vinkler i henhold til summen av dens tiltak. Kilde: Matematikk librettexts.

Når det gjelder sidens plassering, kan to vinkler være:

  • På rad, Når toppunktet og en av sidene har felles.
  • Ved siden av, Hvis de er påfølgende, men ikke -vanlige sider er motsatte, så er de også supplerende.
  • Motsatt av toppunktet, Når de har den vanlige toppunktet, og sidene av vinklene blir forlenget i motsatt retning.
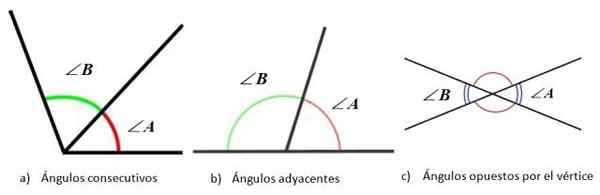Vinkler i henhold til den relative posisjonen mellom sidene. Kilde: f. Zapata

Trekanter

Trekanten er en flat og lukket geometrisk figur, som tilhører polygoners familie, med tre sider som består av linjer som er kuttet to til to, og genererer tre vinkler.

Det kan tjene deg: Bijjektive funksjon: Hva er det, hvordan gjøres det, eksempler, øvelser

Dets grunnleggende elementer er:

  • Hjørner, som er skjæringspunktene for de nevnte linjene.
  • Sider, Totalt 3 og som består av segmentene av linjer som kobles til toppunktene.
  • Interne vinkler, Også i antall 3, hvis sum alltid er lik 180º.

Generelt er sidene betegnet med små bokstaver, toppunktene med store bokstaver og vinklene med små bokstaver, men andre notasjoner er også mulig.

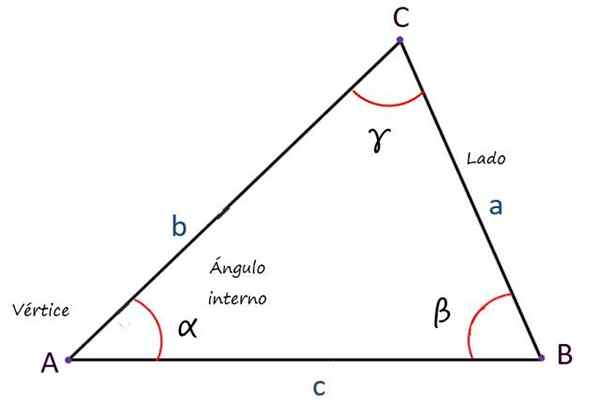Hovedelementer i en trekant. Kilde: f. Zapata

Typer trekanter

Trekanter i henhold til formens form

I henhold til dette kriteriet kan trekanter være:

  • Likeverdige, Hvis de tre sider har samme mål.
  • Likebent, Når bare to av sidene har like mål, mens den tredje er annerledes.
  • Scalene, Hvis de tre sidene har forskjellig størrelse.
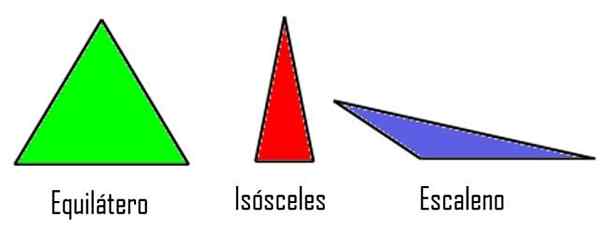Trekanter i henhold til sidene. Modifiserte Wikimedia Commons

Trekanter i henhold til dens indre vinkler

Dette kriteriet er basert på de interne vinkeltypene av trekanten. I følge dette kan en trekant være:

  • Akutangel, Når de tre indre vinklene til trekanten er akutte.
  • Rektangel, Hvis trekanten har en indre målevinkel lik 90º.
  • Stump, En av de indre vinklene til trekanten er stump.
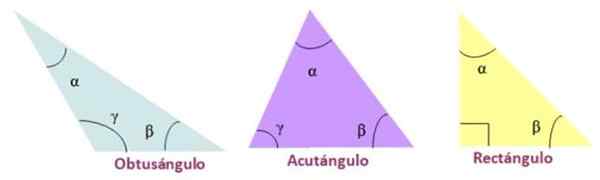Typer trekant i henhold til dens indre vinkler. Kilde: f. Zapata

Bemerkelsesverdige trekantsegmenter

Blant de bemerkelsesverdige segmentene i en hvilken som helst trekant, har de:

  • Median, segment rettet fra et toppunkt, rett til motsatt side.
  • Mediatrix, Det er et segment som tilhører linjen vinkelrett på siden, som krysser midtpunktet på den siden.
  • Bisektor, segment som deler en indre vinkel i to like deler, og som strekker seg til motsatt side av vinkelen.
  • Høyde, segment vinkelrett på siden, som strekker seg til motsatt toppunkt.
Kan tjene deg: LaGrange interpolasjon

Tre medium, tre mediatriser kan spores og så videre.

Triangle Centers

I en hvilken som helst trekant skiller følgende punkter seg (se følgende figur):

  • Baricentro g, også noen ganger kalt centroid Av trekanten er det skjæringspunktet mellom medianene og er alltid interiør for trekanten.
  • Ortocenter h, punkt der de tre høydene krysser hverandre.
  • Circumcentro eller, Det er skjæringspunktet mellom mediatriser. Det kan finnes utenfor trekanten, hvis dette er stump, mens, i rektangelets trekant, eller sammenfaller med midtpunktet til hypotenusen.
  • Incenter, Krysspunkt for trekantbisektorer.
  • Euler rett, Rett som forener barisenteret, ortosenteret og circumcentro, i en hvilken som helst trekant som ikke er liksidig. Det er alltid oppfylt at lengden på HG -segmentet er det dobbelte av GO -segmentet.
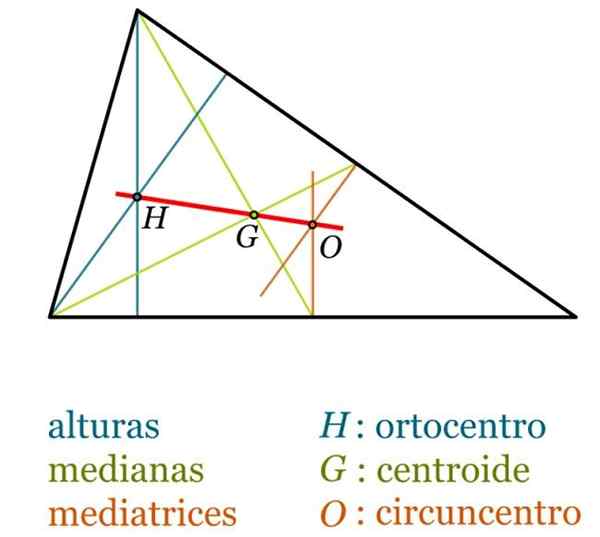Bemerkelsesverdige punkter og segmenter av trekanten. Kilde: Wikimedia Commons

Område av en trekant

For å beregne område A i trekanten brukes følgende formel, av generell art:

A = base × høyde / 2

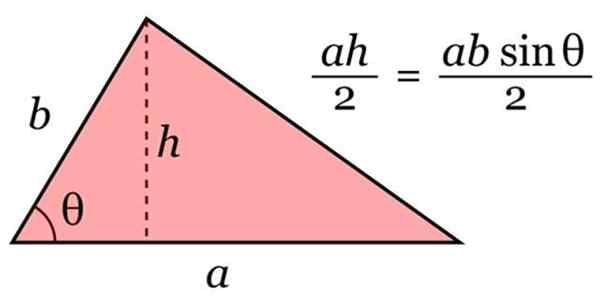Området til trekanten. Kilde: Wikimedia Commons

Herón Formula

Å kjenne lengden på alle sider av trekanten, følgende formel, kjent som Herón Formula, Lar deg finne område A:

Her er sidene av trekanten A, B og C, mens Sp er han semi -perimeter, det vil si halvparten av omkretsen p = a + b + c.

Referanser

  1. Alexander, d. 2013. Geometri. 5. plass. Utgave. Cengage Learning.
  2. Vinkler. Matematikk librettexts. Gjenopprettet fra: Matematikk.Librettexts.org.
  3. Jiménez, René. 2010. Matematikk II (geometri og trigonometri). 2. Utgave. Pearson.
  4. Universformler. Triangel. Gjenopprettet fra: Universoformulas.com.
  5. Zapata, f. Trekanter: Historie, elementer, klassifisering, egenskaper. Hentet fra: Lifer.com.