Euler nummer eller nummer e hvor mye er verdt, egenskaper, applikasjoner

Han Euler nummer eller nummer e Det er en kjent matematisk konstant som ofte vises i en rekke vitenskapelige og økonomiske anvendelser, sammen med antallet π og andre viktige tall i matematikk.

En vitenskapelig kalkulator kaster følgende verdi for nummer E:

Figur 1. Eulers nummer vises ofte i vitenskap. Kilde: f. Zapata.

E = 2.718281828 ..

Men mange flere desimaler er for eksempel kjent:

E = 2.71828182845904523536 ..

Og moderne datamaskiner har tillatt desimal billion til tallet e.

Det er et tall irrasjonell, Noe som betyr at den har en uendelig mengde desimaler uten noe repeterende mønster (sekvens 1828 vises to ganger i begynnelsen og ikke lenger gjentar).

Og det betyr også at tallet e ikke kan oppnås som kvotient for to hele tall.

[TOC]

Historie

Antallet og Han ble identifisert av forskeren Jacques Bernoulli i 1683 da han studerte problemet med sammensatt interesse, men tidligere hadde han indirekte dukket opp i verkene til den skotske matematikeren John Napier, som oppfant logaritmene for 1618.

Imidlertid var det Leonhard Euler i 1727 som ga ham nummer E -navnet og intensivt studerte egenskapene sine. Det er derfor det også er kjent som Euler -nummer og også som et naturlig grunnlag for de neperiske logaritmene (en eksponent) brukt.

Hvor mye er tallet E er verdt?

Tallet E Vale:

E = 2.71828182845904523536 ..

Suspensive poeng betyr at det er en uendelig mengde desimaler, og faktisk er millioner av dem kjent med nåværende datamaskiner.

Representasjoner av nummer e

Det er flere måter å definere e som vi beskriver nedenfor:

Antallet som en grense

En av de forskjellige måtene antallet er uttrykt er den som forskeren Bernoulli fant i sitt arbeid med sammensatt interesse:

Der du må gjøre verdien n Et veldig stort antall.

Det er lett å sjekke, ved hjelp av en kalkulator, at når n Det er veldig stort, det forrige uttrykket har en tendens til verdien av og gitt ovenfor.

Det kan tjene deg: Bijjektive funksjon: Hva er det, hvordan gjøres det, eksempler, øvelser

Vi kan selvfølgelig spørre oss selv hvor stort det kan gjøres n, Så vi prøver med runde tall, for eksempel disse for eksempel:

n = 1000; 10.000 eller 100.000

I det første tilfellet får du E = 2.7169239 .. . I det andre E = 2.7181459 ... og i det tredje er det mye mer nær verdien av og: 2.7182682. Vi kan allerede vises med n = 1.000.000 eller større, tilnærmingen vil bli enda bedre.

På matematisk språk, prosedyren for å lage n Det kommer nærmere og mer til en veldig stor verdi, det kalles det grense til uendelig Og det er betegnet slik:

For å betegne uendelig, brukes "∞" -symbolet.

Antallet som en sum

Det er også mulig å definere nummer E gjennom denne operasjonen:

Tallene som vises i nevneren: 1, 2, 6, 24, 120 ... tilsvarer operasjonen n!, hvor:

n! = n. (N-1).(N-2). (N-3) ..

Og per definisjon 0! = 1.

Det er lett å bekrefte at jo flere tillegg blir lagt til, jo større er antallet nådd og.

La oss gjøre noen tester med kalkulatoren, legge til stadig flere tillegg:

1 +1+ (1/2) + (1/6) = 2.71667

1 +1+ (1/2) + (1/6) + (1/24) = 2.75833

1 +1+ (1/2) + (1/6) + (1/24) + (1/120) = 2.76667

1 +1+ (1/2) + (1/6) + (1/24) + (1/120) + (1/720) = 2.71806

Jo flere vilkår de blir lagt til summen, jo mer er resultatet likt og.

Matematikere utviklet en kompakt notasjon for disse summerene som involverer mange begreper, ved å bruke sumsymbolet σ:

Dette uttrykket leses som "sum av n = 0 til uendelig 1 mellom n factorial".

Tallet E fra det geometriske synspunktet

Antallet E har en grafisk representasjon relatert til området under grafen til kurven:

y = 1/x

Når verdiene til X er mellom 1 og E, er dette området verdt 1, som illustrert i følgende figur:

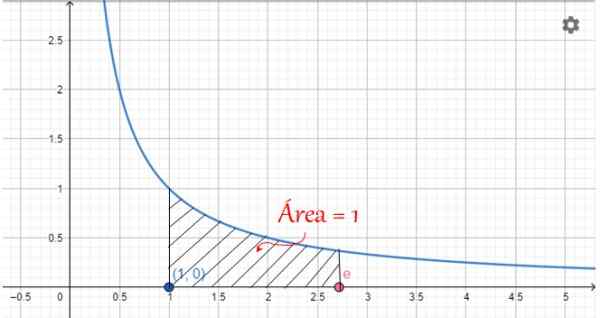Figur 2. Grafisk representasjon av nummer E: Området under kurve 1/x, mellom x = 1 og x = e O'Clock. Kilde: f. Zapata.

Nummer E -egenskaper

Noen av egenskapene til nummer E er:

Kan tjene deg: Voksende funksjon: Hvordan identifisere den, eksempler, øvelser

-Det er irrasjonelt, med andre ord, det kan ikke oppnås bare ved å dele to hele tall.

-Antallet og Det er også en Transcendent nummer, som betyr at og Det er ikke en løsning av noen polynomligning.

-Det er relatert til fire andre kjente tall innen matematikk, nemlig: π, i, 1 og 0, gjennom identiteten til Euler:

og^πi + 1 = 0

-Samtalene komplekse tall kan uttrykkes gjennom e.

-Det utgjør grunnlaget for naturlige eller neperiske logaritmer i dag (John Napiers opprinnelige definisjon skiller seg litt ut).

-Det er det eneste tallet slik at den neperiske logaritmen er verdt 1, det vil si:

 ln e = 1

applikasjoner

Statistikk

Antallet E vises veldig ofte innen sannsynlighet og statistikk, og vises i forskjellige distribusjoner, for eksempel den normale eller Gaussiske, Poisson og andre.

Ingeniørfag

I ingeniørfag er det hyppig, siden eksponentiell funksjon y = e^x Det er for eksempel til stede i mekanikk og elektromagnetisme. Blant de mange applikasjonene vi kan sitere:

-En kabel eller kjede som henger underlagt endene, vedtar formen på kurven gitt av:

y = (e^x + og^-x) /2

-En kondensator C som opprinnelig ble utskrevet, som kobles i serie til en motstand R og en spenningskilde V for å laste, skaffer seg en viss belastning Q avhengig av tiden T gitt av:

Q (t) = cv (1-e^-T/RC)

biologi

Eksponentiell funksjon y = a.og^Bx, Med A og B konstant brukes den til å modellere cellevekst og bakterievekst.

Fysisk

I kjernefysikk er det radioaktive forfallet og bestemmelsen av aldre modellert av radiokarbon datert.

Økonomi

I beregningen av sammensatt interesse oppstår tallet E naturlig.

Anta at du har en viss penger P_enten, å investere det til en årlig rente.

Hvis pengene er igjen i 1 år, etter den tid vil du ha:

P (1 år) = P_enten + P_enten.i = s_enten (1+ i)

Etter enda et år uten å berøre det, vil du ha:

Kan tjene deg: Teoretisk sannsynlighet: Hvordan få det ut, eksempler, øvelser

P (2 år) = P_enten + P_enten.I + (P_enten + P_enten .i) i = p_enten +2 s_enten.i + s_enten.Yo²  = PO (1+I)²

Og på denne måten forbi n år:

P = p_enten (1+i)ⁿ

Husk nå en av definisjonene av E:

Det ser litt ut som uttrykket for P, så det må være et forhold.

Vi vil distribuere den nominelle renten Yo i n Tidsperioder, på denne måten vil den sammensatte renten være I/N:

P = p_enten [1+ (I/N)]ⁿ

Dette uttrykket ser litt mer ut om vår grense, men det er ennå ikke akkurat det samme.

Etter noen algebraiske manipulasjoner kan det imidlertid vises at å gjøre denne endringen av variabel:

h = n/i → i = n/h

Pengene våre P blir:

P = p_enten [1+ (1/h)]^Hei = P_enten [1+ (1/h)]^hYo

Og hva som er blant nøklene, selv om det er skrevet med brevet h, Det er lik argumentet om grensen som definerer tallet E, mangler bare å ta grensen.

La oss gjøre  h → ∞, og hva som er mellom tastene blir forvandlet til tallet og. Dette betyr ikke at vi må vente en uendelig stor tid på å trekke pengene våre.

Hvis vi ser bra ut, når vi gjør det H = n/i Og det vi har gjort det vi virkelig har gjort er å fordele renten i veldig, veldig små perioder: veldig liten:

I = n/h

Dette kalles Kontinuerlig kapitalisering. I dette tilfellet beregnes mengden penger enkelt som følger:

P = p_enten .og^Yo

Hvor jeg er den årlige renten. For eksempel ved å sette inn € 12 til 9 % per år, gjennom kontinuerlig kapitalisering, etter ett år har du:

P = 12 x e^{0.09 × 1} € = 13.€ 13

Med en gevinst på 1.1. 3 €.

Referanser

1. Kos deg med matematikk. Sammensatt interesse: periodisk sammensetning. Gjenopprettet fra: Nytmatimaticas.com.
2. Figuera, J. 2000. Matematikk 1. Diversifisert. Co-bo-utgaver.
3. GARCIA, m. Tallet E i grunnberegningen. Gjenopprettet fra: Matematikk.Ciens.UCV.gå.
4. Jiménez, r. 2008. Algebra. Prentice Hall.
5. Larson, r. 2010. Beregning av en variabel. 9na. Utgave. McGraw Hill.