Oddetall

Hva er rare tall?

De oddetall De er de hele tallene som ikke er delbare med 2. Dette betyr at du med rare mengder ikke kan lage grupper av en 2, for eksempel, hvis noen har 9 karameller å dele med en venn og ikke vil dele noen, vil de berøre 4 karameller og de andre 5.

Noen av de odde tallene er følgende: ... -5, -3, -1, 1, 3, 5, 7, 9, 11, 13 ..  I dette uttrykket indikerer de suspensive punktene at det er flere tall, både venstre og høyre.

Figur 1: Hvordan vite om et tall er merkelig?

Ser du nøye, kan du se at hvert oddetall kan oppnås ved å legge til 2 til foregående nummer. For eksempel, hvis vi legger til 2 til -1, får du 1, hvis vi tjener 1 + 2, er det 3 og så videre.

Det blir også observert at hvis parene er ispedd, inkludert 0, som regnes som et jevnt tall, oppnås settet med hele tall Z.

Det er grunnen til at noe merkelig naturlig tall kan skrives i formen 2n + 1, der n = 0, ± 1, ± 2, ± 3, ± 4, ± 5…, der symbolet ± betyr at det kan tas som positivt eller som negativt.

Når det gjelder større antall, kan det gjenkjennes når det er merkelig, fordi det alltid ender i 1, 3, 5, 7 eller 9. For eksempel er 1571 merkelig og det samme er det negative heltallet -152.489.

Eksempler på oddetall

De odde tallene blir ofte presentert i naturen, og blant dem er nummer 3 av spesiell betydning. La oss se på noen eksempler:

-Det er mange blomster med et rart antall kronblader.

-Vi har 5 fingre på hver hånd.

Kan tjene deg: tilfeldig variabel: konsept, typer, eksempler

-Mennesker har 23 kromosompar.

-Det er de tre lovene i Newton og de tre lovene om termodynamikk.

-Kjernene til atomene som har et rart antall protoner og nøytroner er mindre stabile enn de med et par nummer.

-Magiene er 3.

-I historier og historier vises nummer 3 ofte, for eksempel romaner som De tre musketerer av Alejandro Dumas og i populære historier som De tre brødrene og De tre små griser.

-For den kunstneriske komposisjonen er det samtalen Merkelig regel, som slår fast at en komposisjon med et merkelig antall elementer er mer attraktiv enn en med et par. Det odde tallet legger til dynamikk, mens ett par gir stabilitet.

Figur 2. Et merkelig antall elementer gir dynamikk til et bilde

-En vanlig strategi for å få objektpriser til å se billigere ut er å ende opp 9, for eksempel 2.$ 99, $ 39 og så videre.

-Tallet 13 regnes som uflaks av noen, mens andre tilskriver mystiske egenskaper til 11, begge oddetall.

Primo -tall

Primo -tall, de som bare innrømmer som divisorer selv og 1, er rare, med unntak av 2, som er det eneste fetternummermomentet.

Det er mulig å demonstrere at et hvilket som helst tall kan brytes ned som et produkt av primfaktorer (inkludert disse kreftene), og at denne måten å uttrykke antallet er unikt, bortsett fra i rekkefølgen på faktorene.

For eksempel kan nummer 45 brytes ned som 45 = 3³ x 5.

Odd talloperasjoner

Med de odde tallene utføres alle aritmetiske operasjoner, og noen har enestående egenskaper.

Kan tjene deg: Symbolisering av uttrykk

- Summer og produkter

-Summen av to oddetall resulterer i et jevnt tall: 3+5 = 8; 11+15 = 26; (-10)+ (+6) = - 4.

-Ved å legge til et oddetall med ett dreiemoment, er resultatet rart: 7+2 = 9; 26+ 9 = 35; (-5) + 12 = 7.

-Hvis n første naturlige, rare og påfølgende tall resultatet er n². La oss se dette med litt mer detaljer:

For n = 2: 1 + 3 = 4 = 2²

For n = 3: 1 + 3 + 5 = 9 = 3²

For n = 4: 1 + 3 + 5 + 7 = 16 = 4²

-Når en odd multipliseres med et par, stammer et jevnt tall: 7 x 4 = 28; (-3) x 12 = -36.

-Å multiplisere to oddetall er det også oppnådd en odd: 3 x 5 = 15; (-5) x (+11) = -55.

- Krefter

-Når et positivt tall blir hevet til en merkelig kraft, er det for eksempel et positivt tall: 3³ = 27.

-Ved å heve et negativt tall til en merkelig kraft, er resultatet negativt: (-2)³= (-2) x (-2) x (-2) = -8.

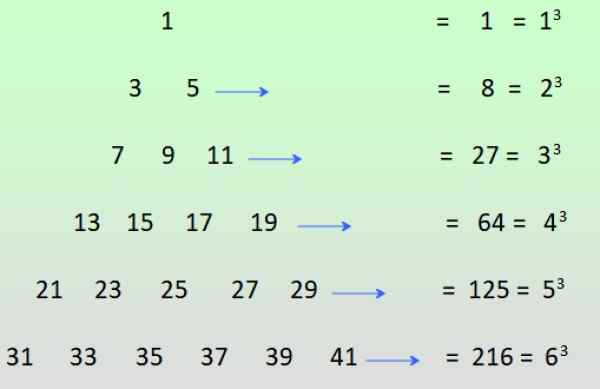
-Odd krefter av positive heltall kan oppnås hvis oddetall er tilgjengelige som vist på figuren og radene legges til:

Figur 3. Få de rare kreftene fra summen av oddetall. Kilde: f. Zapata.

Løste øvelser

- Oppgave 1

Bestem om resultatet av følgende operasjon er jevn eller rart:

(53476890083 + 1987628967) x 13567903

Løsning

For å få svaret trenger du ikke å løpe for å se etter en kalkulator, men for å bruke egenskapene som er sett. La oss se på de siste sifrene i tilleggene, som er henholdsvis 3 og 7:

53476890083  + 1987628967

Dette betyr at de rusavhengige er rare, og vi vet allerede at summen av to oddetall er jevn.

Derfor er figuren som er resultatet av parentesen jevn, og vi vil multiplisere med et tall som ender i 3:

Kan tjene deg: vektor algebra

13567903

Noe som betyr at dette tallet er merkelig.

I egenskapene beskrevet ovenfor ble det fastslått at multipliserende dreiemoment x er et jevnt tall. Derfor er den resulterende operasjonen jevn.

- Oppgave 2

Hvor mye er summen av de første 5 påfølgende oddetall? Og det av de første 50?

Løsning

Summen av de første 5 påfølgende oddetallene er:

1 + 3 + 5 + 7 + 9 = 25

Men hvis vi vil legge til de første 50 på denne måten er det tungvint, så vi skal til eiendommene. De bekrefter at summen av påfølgende oddetall er n². I dette tilfellet n = 50 og summen som blir bedt om er:

femti² = 50 x 50 = 2500.

- Øvelse 3

Når tre påfølgende oddetall legges til, oppnås 237. Hva er tallene?

Løsning

La oss kalle vårt første odde nummer, og det andre og z til det tredje, i henhold til uttalelsen det er oppfylt at:

x + y + z = 237

På algebraisk språk kan ethvert oddetall skrives i skjemaet 2N +1. La oss lage vårt første oddetall:

x = 2n +1

La oss legge til 2 for å få følgende rare:

y = x + 2 = (2n + 1) + 2 = 2n + 3

Og til slutt blir det lagt igjen 2 for å oppnå den tredje rare:

Z = (2n +3) + 2 = 2n + 5

Alt dette legger til:

2n + 1 + 2n + 3 + 2n + 5 = 237

6n + 9 = 237

Det resulterer i en enkel lineær ligning, hvis løsning er:

n = 38

Og nå med verdien av n = 38 er det de tre ordrene:

x = (2 × 38) + 1 = 77

Følgende er rare påfølgende, derfor:

y = 79

Z = 81

Og leseren kan lett bekrefte at summen av de tre er 237.

Referanser

1. Baldor, a. 1986. Aritmetikk. Codex -utgaver og distribusjoner.
2. Nabolag, l. De rare tallene og kreftene til naturlige tall. Hentet fra: Sinewton.org.
3. Strålende. Til og med og rare tall. Gjenopprettet fra: strålende.org.
4. Matematikk 18. Odd talloperasjoner. Hentet fra: Matematikk18.com.
5. Wikipedia. Til og med og rare tall. Gjenopprettet fra: er.Wikipedia.org.