Senoidale bølgefunksjoner, deler, beregning, eksempler

De sinusbølger De er bølgemønstre som matematisk kan beskrives av sinus- og kosinusfunksjonene. De beskriver med rette naturhendelser og variable tegn i tid, for eksempel spenninger generert av elektriske planter og deretter brukt i hjem, bransjer og gater.

Elektriske elementer som motstand, kondensatorer og induktanser, som kobles til sinusformet spenningsinnganger, gir også svar også sinusformet. Matematikk som brukes i beskrivelsen deres er relativt enkel og har blitt grundig studert.

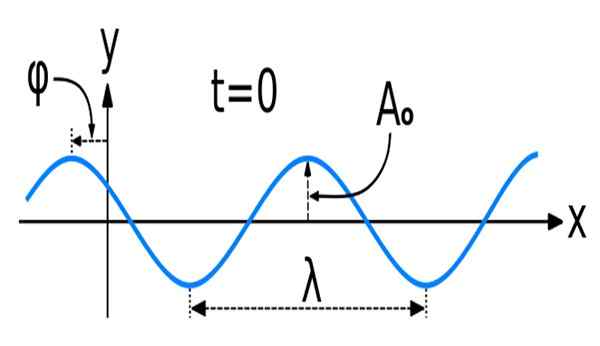
Figur 1. En sinusbølge med noen av de viktigste romlige egenskapene: amplitude, bølgelengde og fase. Kilde: Wikimedia Commons. WAVE_NEW_SINE.SVG: Kraaiennestoriginalt opprettet som en kosinusbølge, av bruker: pelegs, som fil: wave_new.Svgderivativt arbeid: Dave3457 [CC BY-SA 3.0 (https: // creativecommons.Org/lisenser/by-SA/3.0)]

Matematikken til sinusformet eller sinusformet bølger, som de også er kjent, er den av sinus- og kosinusfunksjonene.

Dette er repeterende funksjoner, som betyr periodisitet. Begge har på samme måte, med den forbehold om at kosinuset er fortrengt til venstre med hensyn til brystet i et sykkelrom. Det er observert i figur 2:

Figur 2. Sen X og Cos X -funksjoner blir fortrengt den ene med hensyn til den andre. Kilde: f. Zapata.

Deretter cos x = sin (x + π/2). Ved hjelp av disse funksjonene er en sinusbølge representert. For å gjøre dette plasseres den aktuelle størrelsen på den vertikale aksen, mens tiden i den horisontale aksen er plassert.

Den repeterende kvaliteten på disse funksjonene blir også verdsatt på grafen ovenfor: Mønsteret gjentas kontinuerlig og regelmessig. Takket være disse funksjonene kan du uttrykke spenninger og strømmer av den siniske typen varierende over tid, plassere på den vertikale aksen i stedet for og, en v eller en Yo å representere spenning eller strøm, og på den horisontale aksen i stedet for x, De t vær.

Den mest generelle måten å uttrykke en sinusbølge er:

v (t) = v_m Synd (ωT+φ)

Da vil vi utdype betydningen av dette uttrykket, og definere noen grunnleggende begreper for å karakterisere sinusbølgen.

[TOC]

Fester

Periode, amplitude, frekvens, syklus og fase er konsepter gjelder periodiske eller repeterende bølger og er viktige for å karakterisere dem på riktig måte.

Periode

En periodisk funksjon som de som er nevnt, som gjentas med jevne mellomrom, oppfyller alltid følgende egenskap:

f (t) = f (t + t) = f (t + 2t) = f (t + 3t) = .. .

Hvor T Det er et beløp som heter bølge, Og det er tiden det tar å gjenta en fase av det samme. I internasjonale systemenheter måles perioden i sekunder.

Amplitude

I henhold til det generelle uttrykket av den senoidale bølgen v (t) = v_m sin (ωt+φ), v_m Det er maksimal verdi av funksjonen, som oppstår når sin (ωt+φ) = 1 (Husker at den største verdien som bihule- og kosinusfunksjonen innrømmer at begge er 1). Denne maksimale verdien er nettopp Bølgeamplitude, også kjent som toppamplitude.

I tilfelle en spenning vil bli målt i volt, og hvis det er strøm vil den være i AMPS. I sinusbølgen er bredden konstant, men i andre typer bølge kan amplituden variere.

Kan tjene deg: motstandstermometer: egenskaper, drift, bruk

Syklus

Det er en del av bølgen som er inneholdt i en periode. I forrige figur ble perioden tatt ved å måle den fra to topper eller rygger, men den kan begynne å måles fra andre deler av bølgen, mens de er begrenset av en periode.

Merk i følgende figur som en syklus dekker fra et punkt til et annet med samme verdi (høyde) og samme skråning (helling).

Figur 3. I en sinusbølge foregår en syklus alltid i en periode. Det viktige er at utgangspunktet og slutten er i samme høyde. Kilde: Boylestad. Introduksjon til kretsanalyse. Pearson.

Frekvens

Det er mengden sykluser som oppstår på 1 sekund og er knyttet til argumentet for bihulefunksjonen: ωt. Frekvensen er betegnet som F Og det måles i sykluser per sekund eller Hertz (Hz) i internasjonalt system.

Frekvensen er den omvendte mengden av perioden, derfor:

F = 1/t

Mens frekvens F er relatert til Vinkelfrekvens ω (pulsering) som:

Ω = 2πF

Vinkelfrekvensen er uttrykt i radianer /sekund i det internasjonale systemet, men radianene er dimensjonsløse, og dermed frekvensen F og vinkelfrekvens Ω De har de samme dimensjonene. Merk at produktet ωt gir radianer som et resultat, og må tas i betraktning når du bruker kalkulatoren for å oppnå verdien av Sen ωt.

Fase

Det tilsvarer den horisontale forskyvningen som bølgen opplever, med hensyn til en tid tatt som referanse.

I den følgende figuren er den grønne bølgen avansert med hensyn til den røde i en tid t_d. To sinusformede bølger er i fase Når frekvensen og fasen din er den samme. Hvis fasen er forskjellig, er de i mellomrom. Figur 2 bølger er også utdatert.

Figur 4. Pelied bihulebølger. Kilde: Wikimedia Commons. Ingen maskinlesbar forfatter gitt. Kanjo ~ Commonswiki antatt (basert på krav om opphavsrett)). [Offentlig domene].

Hvis bølgens frekvens er forskjellig, vil de være i fase når fasen ωt+φ være den samme i begge bølger på bestemte øyeblikk.

Senoidal bølgegenerator

Det er mange måter å oppnå et sinusformet signal. Hjemmelagde løp gir dem.

Anvendelse av Faradays lov

En ganske enkel måte å få et sinus signal på er å bruke Faradays lov. Dette indikerer at i en lukket strømkrets, for eksempel en sløyfe, plassert i midten av et magnetfelt, genereres en indusert strøm når magnetfeltet strømmer gjennom den endres over tid. Følgelig a Indusert spenning enten indusert fem.

Strømmen av magnetfeltet varierer hvis sløyfen roteres med konstant vinkelhastighet midt på feltet som er opprettet mellom polene N og S av magneten vist på figuren.

Kan tjene deg: Neptune (planet)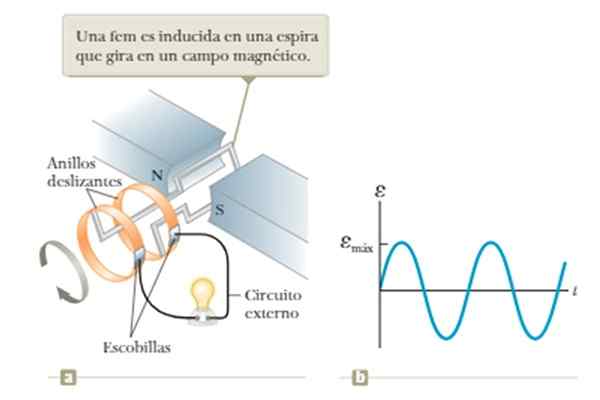Figur 5. Bølgegenerator basert på Faradays induksjonslov. Kilde: Kilde: Raymond A. Serway, Jonh w. Jewett [CC By-SA 4.0 (https: // creativecommons.Org/lisenser/by-SA/4.0)].

Begrensningen av denne operatøren er avhengigheten av spenningen oppnådd med rotasjonsfrekvensen av sløyfen, slik det vil bli mer detaljert i eksempel 1 i eksemplet Senere senere.

Wien Oscillator

En annen måte å få en sinusbølge på, denne gangen med elektron. På denne måten oppnås sinusbølger hvis frekvens og amplitude brukeren kan endre i henhold til deres bekvemmelighet, ved hjelp av bryterjustering.

Figuren viser en sin -signalgenerator, som andre bølgeformer også kan oppnås: Triangular og firkanter blant andre.

Figur 6. En signalgenerator. Kilde: Kilde: Wikimedia Commons. Opgreg på engelsk Wikipedia [CC BY-SA 3.0 (https: // creativecommons.Org/lisenser/by-SA/3.0)].

Hvordan beregne sinusbølger?

For å utføre beregninger som involverer sinusbølger, brukes en vitenskapelig kalkulator som har bihule og kosinus trigonometriske funksjoner, så vel som dens inverse. Disse kalkulatorene har modus for å jobbe vinklene enten i grader eller radianer, og det er enkelt å konvertere den ene veien til den andre. Konverteringsfaktoren er:

180 º = π Radianer.

I henhold til kalkulatormodellen, må du navigere via modusnøkkelen for å finne graden, som lar deg jobbe med trigonometriske funksjoner i grader, eller RAD -alternativet, for å direkte arbeide vinklene i radianer.

For eksempel sin 25 º = 0.4226 med kalkulatoren satt i DEG -modus. Ved å konvertere 25 º til radianer får du 0.4363 radianer og sen 0.4363 rad = 0.425889 ≈ 0.4226.

Oscilloskopet

Oscilloskop. Den har knotter for å justere størrelsen på signalet på et rutenett som vist i følgende figur:

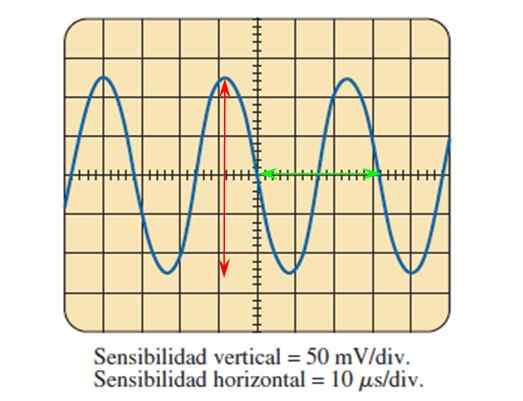Figur 7. Et sinusformet signal målt med et oscilloskop. Kilde: Boylestad.

Gjennom bildet levert av oscilloskopet og kjenne til justering av følsomhet i begge aksene, er det mulig å beregne bølgeparametrene beskrevet ovenfor.

Kan tjene deg: elliptiske galakser: dannelse, egenskaper, typer, eksempler

Figuren viser sinusspenningssignalet som en funksjon av tid, der hver deling av den vertikale aksen er verdt 50 millivolt, mens i den horisontale aksen er hver divisjon verdt 10 mikrosekunder.

Toppen til toppamplitude er å telle divisjonene som bølgen omfatter vertikalt, og hjelper til med den røde pilen:

5 divisjoner telles ved hjelp av den røde pilen, så topp-picospenningen er:

V_pp = 5 divisjoner x 50 mV/divisjon = 250 mV.

Pico Spenning V_p Den måles fra den horisontale aksen, og er 125 mV.

For å finne perioden måles en syklus, for eksempel den som er avgrenset av den grønne pilen, som dekker 3.2 divisjoner, da er perioden:

T = 3.2 divisjoner x 10 mikrosekunder/divisjon = 32 mikrosekunder = 32 μs

Eksempler

Eksempel 1

For generatoren i figur 3, demonstrer fra Faradays lov at den induserte spenningen har sinus. Anta at sløyfen består av n svinger i stedet for en, alt med samme område A og snur med konstant vinkelhastighet ω midt i et magnetfelt B uniform.

Løsning

Faradays lov sier at den induserte FEM ε er:

ε = -n (dφ_B /dt)

Hvor Φ_B Det er strømmen av magnetfeltet, som vil være variabel, siden det avhenger av hvordan sløyfen blir utsatt for feltet hvert øyeblikk. Det negative tegnet beskriver ganske enkelt det faktum at disse kvinnene motsetter seg årsaken som produserer det (Lenz's lov). Flyten på grunn av en enkelt sløyfe er:

Φ_B = B.TIL.cos θ

θ er vinkelen som den normale vektoren til loopens plan dannes med feltet B Når rotasjonen finner sted (se figur), varierer denne vinkelen naturlig som:

θ = ωt

Så det: Φ_B = B.TIL.cos θ = b.TIL.Cos ωt. Nå må du bare utlede dette uttrykket med hensyn til tid og med det er den induserte FEM oppnådd:

ε = -n.d (b.TIL.Cos ωt) /dt

Som feltet B Det er ensartet og spaseområdet varierer ikke, de forlater derivatet:

ε = -nba. D (Cos ωt) /dt = ωnba. Sen ωt

Eksempel 2

En sløyfe har et område på 0.100 m² og vend deg til 60.0 Rev/s, med sin rotasjonsakse vinkelrett på et jevnt magnetfelt på 0.200 t. Å vite at spolen har 1000 svinger for å finne: a) den maksimale FEM som genereres, b) orienteringen av spolen i forhold til magnetfeltet når det maksimale induserte FEM oppstår.

Figur 8. En spiral av n runder brutt i midten av et jevnt magnetfelt og genererer et sinus signal. Kilde: r. Serway, Physics for Science and Engineering. Volum 2. Cengage Learning.

Løsning

a) Maksimal FEM er ε_Maks = Ωnba

Før du fortsetter med å erstatte verdiene, må frekvensen på 60 rev/s til enheter i det internasjonale systemet passerer. Det er kjent at 1 revolusjon tilsvarer en sving eller 2p -radianer:

60.0 Rev/s = 120p radianer/s

ε_Maks = 120p radianer x 1000 runder x 0.200 T x 0.100 m² = 7539.82 V = 7.5 kV

b) Når denne verdien oppstår Sen ωt = 1 derfor:

ωt = θ = 90º,

I dette tilfellet er spiralplanet parallelt med B, slik at den normale vektoren til nevnte plan danner 90º med feltet. Dette skjer når den svarte vektoren i figur 8 er vinkelrett på den grønne vektoren som representerer magnetfeltet.

Referanser

1. Boylestad, r. 2011. Introduksjon til kretsanalyse. 12. Utgave. Pearson. 327-376.
2. Figueroa, d. 2005. Elektromagnetisme. Fysisk serie for vitenskap og ingeniørfag. Volum 6. Redigert av d. Figueroa. Simon Bolivar University. 115 og 244-245.
3. Figueroa, d. 2006. Fysikklaboratorium 2. Redaksjonell Equinox. 03-1 og 14-1.
4. Sinusbølger. Gjenopprettet fra: IessierradeGara.com
5. Serway, r. 2008.Fysikk for vitenskap og ingeniørfag. Volum 2. Cengage Learning. 881-884