Stasjonære bølgerformler, egenskaper, typer, eksempler

De stående bølger De er bølger som sprer seg i en begrenset halvdel, går og kommer i en del av plassen, i motsetning til reisebølger, som når de forplanter beveger seg bort fra kilden som oppsto dem og ikke kommer tilbake til den.

De er grunnlaget for lydene som produseres i musikkinstrumentene, siden de lett oppstår på de faste strengene, enten i en av dens ender eller begge deler. De er også skapt i anspente membraner som trommer eller inne i rør og strukturer som broer og bygninger.

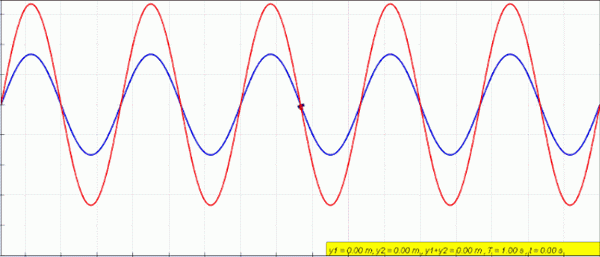Animasjon av en stasjonær (rød) bølge skapt av superposisjonen av en venstre (blå) og høyre bølge (grønn). Kilde: Lookangmany Takk til forfatter av Original Simulation = Wolfgang Christian og Francisco Schembre Forfatter av Easy Java Simulation = Francisco Schembre/CC By-SA (https: // CreativeCommons.Org/lisenser/by-SA/4.0)

Når du har et fast tau i begge ender, for eksempel en gitar, er bølger laget med identisk amplitude og frekvens, som reiser i motsatte sanser og kombinerer å produsere et fenomen som kalles innblanding.

Hvis bølgene er i fase, er ryggene og dalene justert og resulterer i en bølge med dobbel amplitude. I så fall er det snakk om konstruktiv interferens.

Men hvis bølgene som forstyrrer seg er utenfor fase, møter ryggene til en andres daler og amplituden som resulterer er null. Det er da en destruktiv forstyrrelse.

[TOC]

Formler og ligninger

Hovedelementene i bølgen for å representere den i rom og tid er dens amplitude A, dens bølgelengde λ og dens vinkelfrekvens ω.

Elementer av en bølge. Kilde: Wikimedia Commons.

I matematisk representasjon er det foretrukket å bruke k, enn Bølgenummer o Antall ganger bølgen per enhet skjer. Derfor er det definert gjennom lengden på λ -bølgen som er avstanden mellom to daler eller to rygger:

K = 2π/ λ

Mens vinkelfrekvens Det er relatert til perioden eller varigheten av en fullstendig svingning, for eksempel:

Ω = 2π/ t

Og også frekvensen f er gitt av:

F = ω / 2π

Derfor:

F = 1/t

I tillegg beveger bølgene seg med hastighet v i følge:

v = λ.F

Matematisk uttrykk for den stasjonære bølgen

Matematisk kan vi uttrykke en bølge gjennom bihulefunksjonen eller kosinusfunksjonen. Anta at det er bølger av lik amplitude A, bølgelengde λ og frekvens ω, sprer seg langs et tau og i motsatte sanser:

og₁ = En synd (kx - ωt)

og₂ = En synd (kx + ωt)

Når vi legger dem til, finner vi den resulterende bølgen og_R:

og_R = y₁ + og₂ = En sen (kx - ωt) + en sin (kx + ωt)

Det er en trigonometrisk identitet for å finne summen:

Kan tjene deg: det som er relativt og absolutt ruhet?

sin α + sin β = 2 sin (α + β)/2 . cos (α - β)/2

Gjennom denne identiteten, den resulterende bølgen og_R er til overs:

og_R = [2a Sen KX] . cos ωt

Plassering av noder og mage

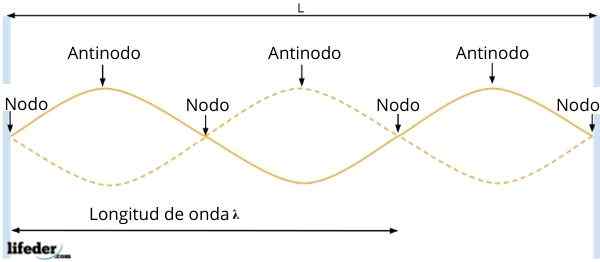Antinodos eller mage og noder

Den resulterende bølgen har amplitude til_R = 2ase KX, som avhenger av partikkelens plassering. Deretter, på punktene som Sen Kx = 0, blir amplituden til bølgen kansellert for, det vil si at det ikke er noen vibrasjon.

Disse punktene er:

Kx = π, 2π, 3π ..

Som k = 2 π/ λ:

(2 π/ λ) x = π, 2π, 3π ..

x = λ/2, λ, 3λ/2 ..

I slike punkter oppstår ødeleggende interferens og de kalles noder. De er atskilt med en avstand lik λ/2, som trukket fra forrige resultat.

Og mellom to påfølgende noder er antinodos eller mage, der bølgenes amplitude er maksimal, siden den konstruktive interferensen oppstår. De oppstår når:

sin kx = ± 1

Kx = ± π/2, 3π/2, 5π/2 ..

Igjen k = 2 π/ λ og deretter:

x = λ /4, 3λ /4, 5λ /4, ..

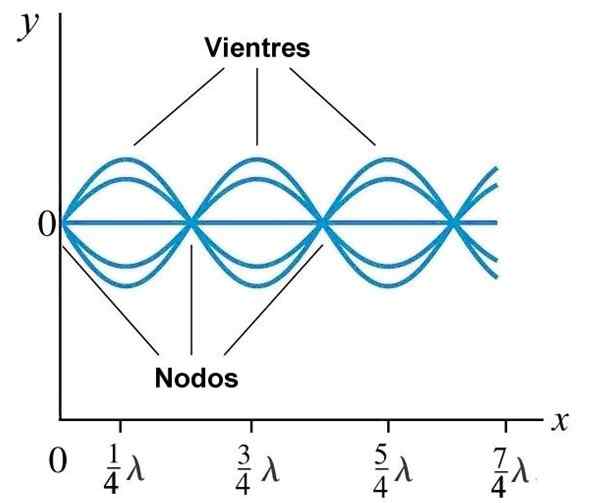Mage eller antinoder og noder i en stasjonær bølge generert på et tau med fast ende ved x = 0. Kilde: Wikimedia Commons.

Normale modus på et tau

Grenseforholdene på tauet bestemmer hvordan bølgelengder og frekvenser er. Hvis et tau i lengde L er fikset av de to ender, kan det ikke vibrere med noen frekvens, fordi punktene der tauet er faste allerede er noder.

I tillegg er skillet mellom tilstøtende noder λ/2, og mellom node og mage er det λ/4, på denne måten bare for visse bølgelengder produseres stasjonære bølger: de der et heltall n av λ/2 inni er justert av de:

(λ/2) = l, med n = 1, 2, 3, 4 .. .

Derfor:

λ = 2l/n

Harmonikken

De forskjellige verdiene som er tatt λ kalles harmonikk. Dermed har vi:

-Første harmonisk: λ = 2l

-Andre harmoniske: λ = l

-Tredje harmonisk: λ = 2 l/3

-Harmonisk rom: λ = l/2

Og så videre.

Hastighet og frekvens

Selv om den stasjonære bølgen ikke ser ut til å bevege seg, er ligningen fremdeles gyldig:

v = λ. F

Derfor:

v = (2l/n) . F

F = nv/2l

Nå kan det påvises at hastigheten som en bølge beveger seg i et tau, avhenger av T -spenningen i samme og dens lineære tetthet av masse μ (masse per lengdeenhet) som:

Derfor:

Kan tjene deg: døde belastninger: egenskaper, beregning, eksempler

Funksjoner ved stasjonære bølger

-Når bølgene er stasjonære, sprer den resulterende bølgen seg ikke som komponentene, som går fra et sted til et annet. Det er punkter der y = 0 fordi det ikke er noen vibrasjon: nodene, med andre ord, amplituden til_R Det er null.

-Det matematiske uttrykket av en stasjonær bølge består av produktet av en romlig del (som avhenger av X -koordinaten eller romkoordinatene) og en tidsmessig del.

-Blant nodene svinger den resulterende svarte bølgen på ett sted, mens bølgene som går fra et sted til et annet er utdatert der.

-Bare i nodene transporteres ikke energi, siden dette er proporsjonalt med kvadratet av amplituden, men er fanget mellom nodene.

-Avstanden mellom tilstøtende noder er halvparten av bølgelengden.

-Punktene der tauet er fikset, anses også som noder.

Folkens

Stasjonære bølger i en dimensjon

Bølgene i et fast tau er eksempler på stasjonære bølger i en dimensjon, hvis matematiske beskrivelse vi tilbød i de forrige seksjonene.

Stasjonære bølger i to og tre dimensjoner

Stasjonære bølger kan også presenteres i to og tre dimensjoner, og være en litt mer kompleks matematisk beskrivelse.

Racing Ondas eksempler

Faste strenger

-En streng festet av ekstrem som svinges for hånd eller med det ene stempelet av det andre genererer stasjonære bølger langs dens lengde.

Musikkinstrumenter

Stasjonære bølger er laget i musikkinstrumenter som Violoncello. Kilde: Pixabay.

-Når du spiller strenginstrumenter som gitar, harpe, fiolin og piano.

Stlover -bølger er også laget i luftrør, for eksempel orgelrør.

Bygninger og broer

Stasjonære bølger oppstår i strukturer som broer og bygninger. En bemerkelsesverdig sak var den av Tacoma Narrows Suspension Bridge nær byen Seattle, USA. Kort tid etter å ha blitt innviet i 1940, kollapset denne broen på grunn av de stasjonære bølgene som ble opprettet inne i vinden.

Vindfrekvensen matchet med den naturlige frekvensen av broen, og skapte i stasjonære bølger i dette, som økte amplituden til broen kollapset. Fenomenet er kjent som resonans.

Det kan tjene deg: lett refleksjon

Seiches

I havnene er det et veldig nysgjerrig fenomen som heter Seiche, der havets bølger produserer store svingninger. Dette er fordi vannet i havnen er ganske lukket, selv om det oseaniske vannet trenger gjennom så ofte gjennom inngangen til havnen.

Portvann beveger seg med sin egen frekvens, så vel som havets hav. Hvis begge farvannene samsvarer med frekvensene sine, er det en stor stasjonær bølge på grunn av resonans, som skjedde med Tacoma Bridge.

De Seiches De kan også forekomme i innsjøer, reservoarer, svømmebassenger og andre vannmasser begrenset av overflater.

Fisketanker

Stasjonære bølger kan opprettes i en fiskebolle som transporteres av en person, hvis frekvensen personen er lik frekvensen av svingen av vannet.

Trening løst

Gitartauet har L = 0.9 m og lineær deigtetthet μ = 0.005 kg/m. Den blir utsatt for 72 N spenning og dens vibrasjonsmodus er den som viser figuren, med amplitude 2a = 0.5 cm.

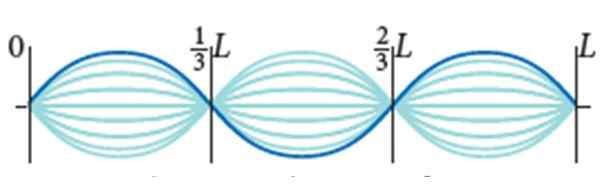Stasjonære bølger på et gitartau. Kilde: Bauer, W. Fysisk.

Finne:

a) Forplantningshastighet

b) bølgefrekvens

c) Den tilsvarende stasjonære bølge -ligningen.

Løsning på

Gjennom:

Er oppnådd;

V = [72 n/(0.005 kg/m)]^1/2  = 120 m/s.

Løsning b

Avstanden mellom to tilstøtende noder er λ/2, derfor:

(2/3) l - (1/3) l = λ/2

(1/3) L = λ/2

λ = 2L/3 = 2 x 0.90 m / 3 = 0.60 m.

Som v = λ.F

F = (120 m/ s)/ 0.60 m = 200 s^-1= 200 Hz.

Løsning c

Ligningen er:

og_R = [2a Sen KX] . cos ωt

Vi må erstatte verdier:

K = 2π/ λ = k = 2π/ 0.60 m = 10 π/3

F = ω / 2π

Ω = 2π x 200 Hz = 400 π Hz.

2A -amplituden er allerede gitt av uttalelsen:

2a = 0.5 cm = 5 x 10 ^-3 m.

Derfor:

og_R = 5 x 10 ^-3 m . sin [(10π/3) x] . cos (400πt) =

= 0.5 cm . sin [(10π/3) x] . cos (400πt)

Referanser

1. Bauer, w. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill.
2. Figueroa, d. (2005). Serier: Fysikk for vitenskap og ingeniørfag. Volum 7. Bølger og kvantefysikk. Redigert av Douglas Figueroa (USB).
3. Giancoli, d.  2006. Fysikk: Prinsipper med applikasjoner. 6. Ed Prentice Hall.
4. Serway, r., Jewett, J. (2008). Fysikk for vitenskap og ingeniørfag. Volum 1. 7. Ed. Cengage Learning.
5. Tipler, s. (2006) Fysikk for vitenskap og teknologi. 5. utg. Volum 1. Redaksjon tilbake.
6. Wikipedia. Seiche. Gjenopprettet fra: er.Wikipedia.org.