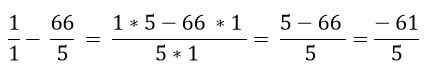Papomudas

Hva er papomudas?

Han Papomudas Det er en prosedyre for å løse algebraiske uttrykk. Forkortelsen indikerer prioriteringsrekkefølgen: parentes, krefter, multiplikasjon, divisjon, tillegg og subtraksjon. Ved hjelp av dette ordet kan du enkelt huske rekkefølgen et uttrykk som sammensatte av flere operasjoner må løses.

Generelt kan du i numeriske uttrykk finne flere aritmetiske operasjoner sammen, for eksempel summer, subtraksjon, multiplikasjoner og divisjoner, som også kan være brøk, krefter og røtter. For å løse dem er det nødvendig å følge en prosedyre som garanterer at resultatene vil være riktige.

Et aritmetisk uttrykk som består av en kombinasjon av disse operasjonene, må løses i henhold til prioritering av orden, også kjent som hierarkiets hierarki, etablert for lenge siden i universelle konvensjoner. Dermed kan alle mennesker følge samme prosedyre og oppnå samme resultat.

Kjennetegn

Papomudas er en standardprosedyre som etablerer rekkefølgen som må følges når et uttrykk må gis, som er sammensatt av en kombinasjon av operasjoner som subtraksjonssum, multiplikasjon og inndeling.

Denne prosedyren fastsetter prioriteringsrekkefølgen i en operasjon i forhold til de andre på det tidspunktet de vil være; det vil si at hver operasjon har et hierarkisk skifte eller nivå som skal løses.

Rekkefølgen som de forskjellige operasjonene av et uttrykk må løses, gis av hvert forkortelse av ordet papomudas. På denne måten må du:

1. PA: Parenteser, firkantede parenteser eller nøkler.
2. PO: Powers and Roots.
3. MU: Multiplikasjoner.
4. D: Divisjoner.
5. A: Tillegg eller summer.
6. S: subtraksjoner eller subtraksjon.

Denne prosedyren kalles også på engelsk som Pemdas; Å enkelt huske dette ordet er assosiert med uttrykket: "Unnskyld min kjære tante Sally”, Der hver innledende bokstav tilsvarer en aritmetisk operasjon, på samme måte som papomudas.

Hvordan løse dem?

Basert på hierarkiet etablert av papomudas for å løse driften av et uttrykk, er det nødvendig å oppfylle følgende ordre:

• For det første må alle operasjoner som er innenfor grupperingssymboler, for eksempel parentes, nøkler, parentes og brøkdeler, løses. Når det er grupperingssymboler i andre, bør du begynne å beregne fra innsiden.

Kan tjene deg: kvadratiske suksesser: eksempler, regel og øvelser løst

Disse symbolene brukes til å endre rekkefølgen som operasjoner løses, fordi det som alltid er innenfor disse, må alltid løses.

• Da løses kreftene og røttene.
• På tredjeplass løses multiplikasjoner og divisjoner. Disse har samme prioriteringsrekkefølge; Derfor, når disse to operasjonene finnes i et uttrykk, må den som vises først løses, og lese uttrykket fra venstre mot høyre.
• Til syvende og sist løses summen og subtraksjonen, som også har samme prioriteringsrekke.
• Operasjoner skal aldri blandes når du leses fra venstre mot høyre, du må alltid følge prioriteringsrekkefølgen eller hierarkiet etablert av papomudas.

Det er viktig å huske at resultatet av hver operasjon må plasseres i samme rekkefølge i forhold til andre, og alle mellomtrinn må skilles med et tegn til det når det endelige resultatet.

applikasjon

Papomudas -prosedyre brukes når du har en kombinasjon av forskjellige operasjoner. Når du tar hensyn til hvordan de løses, kan dette brukes i:

Uttrykk som inneholder summer og subtraksjoner

Det er en av de enkleste operasjonene, fordi begge har samme prioriteringsrekkefølge, slik at den må løses fra venstre til høyre i uttrykket; For eksempel:

22 -15 + 8 +6 = 21.

Uttrykk som inneholder summer, subtraksjon og multiplikasjoner

I dette tilfellet er den høyeste prioriterte operasjonen multiplikasjon, deretter løses summen og subtraksjonen (den som er først i uttrykket). For eksempel:

6 _* 4 - 10 + 8 _* 6 - 16 + 10 _* 6

= 24 -10 + 48 - 16 + 60

= 106.

Uttrykk som inneholder sum, subtraksjonsmultiplikasjon og inndeling

I dette tilfellet er det en kombinasjon av alle operasjoner. Det begynner med å løse multiplikasjonen og inndelingen som har overlegen prioritet, deretter summer og subtraksjon. Lese uttrykket fra venstre mot høyre løses det i henhold til hierarkiet og posisjonen i uttrykket; For eksempel:

Kan tjene deg: Mamma

7 + 10 _* 13 - 8 + 40 ÷ 2

= 7 + 130 - 8 + 20

= 149.

Uttrykk som inneholder sum, subtraksjon, multiplikasjon, inndeling og krefter

I dette tilfellet er et av tallene forhøyet til en kraft, som innenfor prioriteringsnivået må løses først, og deretter løse multiplikasjoner og inndelinger, og til slutt summer og subtraksjon:

4 + 4² _* 12 - 5 + 90 ÷ 3

= 4 + 16 _* 12 - 5 + 90 ÷ 3

= 4 + 192 - 5 + 30

= 221.

I likhet med kreftene har røttene også den andre prioriteringsrekkefølgen; Derfor, i uttrykk som inneholder dem, må de først løses enn multiplikasjoner, divisjoner, summer og subtraksjon:

5 _* 8 + 20 ÷ √16

= 5 _* 8 + 20 ÷ 4

= 40 + 5

= 45.

Uttrykk som bruker grupperingssymboler

Når skilt brukes, for eksempel parentes, nøkler, parentes og brøkstenger, som er innenfor disse, blir det løst først, uavhengig av prioriteringens rekkefølge som den inneholder i forhold til de utenfor dette, som om den vil håndtere en egen uttrykk:

14 ÷ 2 - (8 - 5)

= 14 ÷ 2 - 3

= 7 - 3

= 4.

Hvis det er flere operasjoner, må disse løses ved hierarkisk orden. Deretter løses de andre operasjonene som utgjør uttrykket; For eksempel:

2 + 9 * (5 + 2³ - 24 ÷ 6) - 1

= 2 + 9 * (5 + 8 - 4) - 1

= 2 + 9 * 9 - 1

= 2 + 81 - 1

= 82.

I noen uttrykk brukes grupperingssymboler i andre, for eksempel når det er nødvendig å endre tegnet på en operasjon. I disse tilfellene må det begynne med å løse fra innsiden og ut; det vil si å forenkle grupperingssymbolene som er i sentrum av et uttrykk.

Generelt er rekkefølgen å løse operasjoner som finnes i disse symbolene: først løse det som er innenfor parenteser (), deretter parentes [] og til slutt nøklene .

90 - 3_*[12 + (5_*4) - (4_*2)]

= 90 - 3_* [12 + 20 - 8]

Kan tjene deg: Teoretisk sannsynlighet: Hvordan få det ut, eksempler, øvelser

= 90 - 3 _* 24

= 90 - 72

= 18.

Øvelser

Første trening

Finn verdien av følgende uttrykk:

tjue² + √225 - 155 + 130.

Løsning

Påføring av papomudas, må kreftene og røttene løses først, og deretter legger til og subtraksjon. I dette tilfellet tilhører de to første operasjonene samme orden, så den som først er løst, fra venstre til høyre:

tjue² + √225 - 155 + 130

= 400 + 15 -155 + 130.

Legg deretter til og subtraksjon, og starter til venstre også:

400 + 15 -155 + 130

= 390.

Andre trening

Finn verdien av følgende uttrykk:

[- (6³ - 3⁶) ÷ (8 _* 6 ÷ 16)].

Løsning

Det begynner med å løse operasjonene som er innenfor parentesene, etter den hierarkiske ordenen de har i henhold til papomudas.

Først løses kreftene til den første parentesen. Når de tilhører samme rekkefølge, løses den første operasjonen av uttrykket:

[- (6³ - 3⁶) ÷ (8 _* 6 ÷ 16)]

= [- (216- 729) ÷ (8 _* 6 ÷ 16)]

= [ - (216 - 729) ÷ (48 ÷ 16)]

= [- (-513) ÷ (3)].

Ettersom operasjoner innen parenteser allerede er løst, videreføres nå divisjonen som har det største hierarkiet:

[- (-513) ÷ (3)] = [- (-171)]]].

Til slutt indikerer parentesen som skiller minus (-) tegnet fra resultatet, som i dette tilfellet er negativt, at en multiplikasjon av disse tegnene må gjøres. Dermed er resultatet av uttrykket:

[- (-171)] = 171.

Tredje øvelse

Finn verdien av følgende uttrykk:

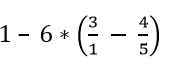
Løsning

Fraksjonene som er innenfor parentesen blir løst:

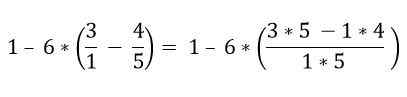
Innenfor parentesen er det flere operasjoner. Multiplikasjonene løses først og deretter subtraksjonene; I dette tilfellet blir brøkdelen betraktet som et grupperingssymbol og ikke som en inndeling, så operasjonene til den øvre og nedre delen må løses:

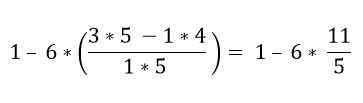
Ved hierarkisk orden må multiplikasjon løses:

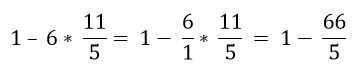
Endelig løses subtraksjonen: