Pentadecágono -elementer, klassifisering, egenskaper, trening

EN PentadecTilbake Det er en flat figur bygget med femten rette segmenter og lukket. Denne typen figurer kalles Polygon og de er navngitt i henhold til mengden sider som har.

Trekanten, med tre sider og den firkantede, av fire, er eksempler på veldig kjente polygoner, men polygonene kan ha flere sider.

Figur 1.  Vanlig femkant med røde hjørner. Kilde: Wikimedia Commons.

De grunnleggende elementene i Pentadecágono er de samme som en hvilken som helst polygon, uavhengig av mengden sider den har. Disse elementene er:

-Sider, som er segmentene som utgjør pentadecágono for totalt 15.

-Hjørner, også 15, som er endene på de tilstøtende sidene.

-Interne vinkler, De som er dannet i pentadecágono mellom to tilstøtende sider.

-Eksterne vinkler, dannet mellom den ene siden og forlengelsen av en av sidene på rad.

-Diagonaler, Linjesegmentene som går sammen med to ikke -adjacent hjørner.

[TOC]

Klassifisering

En pentadecágono kan være regelmessig enten uregelmessig, Avhengig av størrelsen på sidene og målet på dens indre vinkler. Hvis du har alle sidene og de like indre vinklene - Quilátero og Equiangle - er det regelmessig, som vist i figur 1, ellers er det uregelmessig.

Det kan også klassifiseres som konveks enten konkav. En konkav Pentagon har en eller flere indre vinkler større enn 180 º, mens en alltid har konveks innvendige vinkler mindre enn 180º. Den vanlige femkanten er konveks.

Nok et klassifiseringskriterier vurderes hvis det ikke er sammenhengende sider - eller deres utvidelser - er kuttet eller ikke. Når de ikke er kuttet, som for figur 1, sies det at det er en enkel pentadecágon. Og hvis de er kuttet, er det sammensatt.

Det kan tjene deg: analytisk geometri

Den vanlige Pentagon

Den vanlige Pentagon, hvis sider og indre vinkler har samme mål, er en figur av stor symmetri, fordi følgende tilleggselementer er definert til de som tidligere er beskrevet:

-Senter: Poenget med at ekvidista av toppunktene og sidene.

-Radio: Avstanden fra sentrum til en av de vanlige Pentagon -toppunktene.

-Sentral vinkel: Den som har toppunktet i midten av figuren og sidene passerer gjennom to tilstøtende toppunkter.

-Apothem, Det er det vinkelrett segmentet som blir med i midten av den ene siden med midten av figuren.

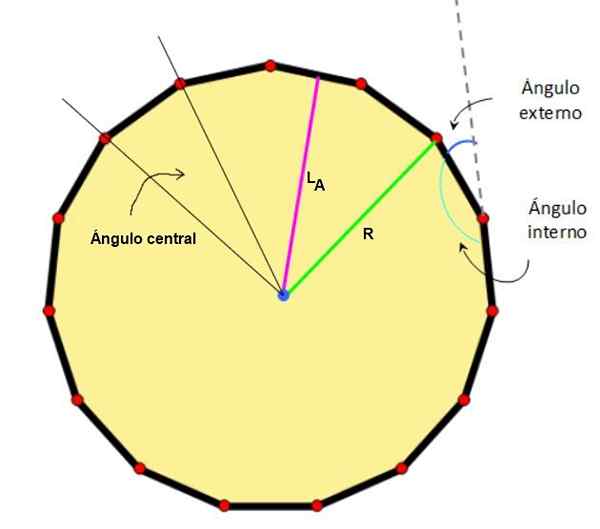Figur 2. Center, Apothem, radio og bemerkelsesverdige vinkler på en pentadecágono. Kilde: Wikimedia Commons/F. Zapata.

- Kjennetegn ved vanlig femkant

Interne vinkler

Følgende formel brukes til å beregne mål I av de indre vinklene til en hvilken som helst vanlig polygon, hvor n Det er antall sider:

I denne formelen, tiltaket jeg kommer i grader, for å uttrykke det i radianer, multipliseres det med π/180 -faktoren. La oss se hva som er målet på de interne vinklene til den vanlige Pentagon, og erstatter n = 15:

I = [(15-2) × 180º]/15 = 156º º

Tilsvarer 13π/15 radianer. Siden de indre vinklene til den vanlige Pentagon er mindre enn 180º, er det en konveks polygon.

Sum av interne vinkler

Det er mulig å beregne summen av de interne vinklene ved å bruke følgende formel:

S = (n-2) x 180º

Som alltid representerer N antall sider. Denne formelen er gyldig for n = 3, 4, 5 .. .

Gjør n = 15 vi får:

S = (15 - 2) x 180º = 2340º

Eksterne vinkler

En intern vinkel og en ekstern vinkel er supplerende, det vil si summen er 180º, som nevnt i figur 2. Derfor måler en ytre vinkel på Pentadecágono:

Kan tjene deg: konjugert binomial: hvordan det løses, eksempler, øvelser

180 º - 156º = 24º.

Omkrets og område

Omkretsen er målet på polygonkonturen og tilsetter lett alle sider. Ja til Det er lengden på siden, det er nok å multiplisere med n, Antall sider.

For en vanlig femkant av side A er omkretsen P:

P = 15A

Hvis det er en uregelmessig figur, der målet på sidene er forskjellig, legger omkretsen til lengden på alle sidene.

Når det gjelder området, kan vi beregne det på flere måter. For eksempel har vi formelen som lar deg få tak i den å vite lengden A på sidene:

Utfører de angitte operasjonene, det forblir omtrent:

A = 17.6426⋅a²

Det er et annet alternativ, gjeldende for vanlige polygoner. Det handler om å dele dem inn i basetrekanter som er lik polygonen til. Høyden på trekanten er lengden på apothem l_TIL, definert ovenfor.

Området med nevnte trekant beregnes med den velkjente formelen: base x høyde /2. På denne måten er det ene trekantområdet:

Område = a. L_TIL /2

For å ha det totale arealet av polygon, er det nok å multiplisere med antall sider n, som i dette tilfellet er 15:

A = 15⋅a⋅ l_TIL /2

Og siden omkretsen av figuren er p = 15⋅a, så:

A = p⋅ l_TIL /2

Diagonaler

Diagonalene er segmentene som forener to ikke -samtykke vertikaler, som nevnt ovenfor. Å vite hvor mange diagonaler en vanlig polygon har av n Sider, inkludert Pentadecágono, er det følgende formel:

Hvor D er antall diagonaler.

Nå erstatter vi n = 15, for å få de totale diagonalene:

Kan tjene deg: vanlige polygoner: egenskaper, elementer, vinkler, eksempler

D = [15 × (15-3)]/2 = 90 diagonaler.

Konstruksjon med regel og kompass

Pentadecágono er bygget med regel og kompass fra en omkrets. 360º må deles inn i 15 like deler av 24º hver. Først utføres hjelpekonstruksjonene som er angitt i animasjonen for å oppnå en vinkel på 60º, som er delt i sving til 36º og 24º.

Figur 3. Konstruksjon med regel og kompass av en vanlig femkant. Kilde: Wikimedia Commons.

Trening løst

Hvis omkretsen til en pentadecágono registrert i en sirkel av radius r er 12,56 cm. Regne ut:

a) radioen.

b) Ditt område.

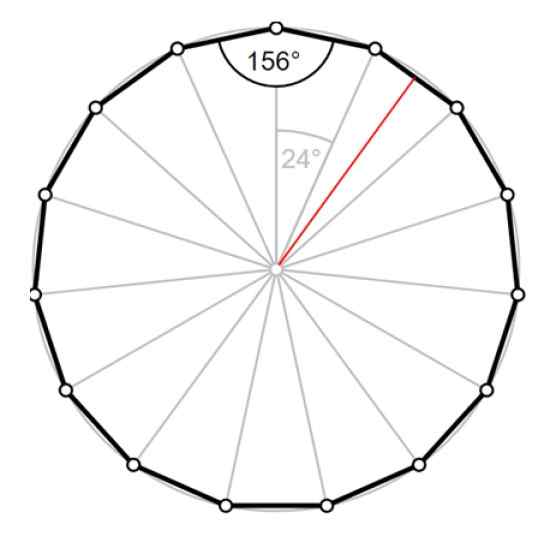Figur 4. Pentadecágono: Sentral vinkel, indre vinkel og rød apotema. Kilde: Wikimedia Commons/F. Zapata.

Løsning på

Omkretsen er p = 15⋅a = 12.56 cm, derfor siden av pentadecágono er 0.8373 cm. Radioen Vi kan beregne det ved hjelp av en av trekantene i figur 4.

Apothem l_TIL tilsvarer høyden på trekanten, tegnet i rødt, som deler vinkelen på 24º i to vinkler på 12º hver.

Det er to høyre trekanter med en indre vinkel på 12º hver, og for noen av dem kan vi bruke trigonometri for å finne hypotenusen, som er radiusens lengde R.

Denne måten:

Sen 12º = (a /2) /r

R = (a /2) /sen 12º = (0.8373 cm / 2) / sen12º = 2.01 cm.

Løsning b

Vi kan beregne Pentadecágono -området ved å bruke formelen:

A = p⋅ l_TIL /2

Vi kjenner allerede omkretsen P = 12.56 cm, og lengden på apothem beregnes av tangenten eller 12º cosinen:

Cos 12º = l_TIL / R

L_TIL = R. cos 12 º = 2.01 cm. cos 12 º = 1.97 cm

Erstatte:

A = 12.56 cm⋅ 1.97 cm /2 = 12.35 cm²

Referanser

1. Alexander, d. 2013. Geometri. 5. plass. Utgave. Cengage Learning.
2. Lær matematikk. Geometriske figurer. Gjenopprettet fra: Rodrigoanchorena.Wixsite.com.
3. Sangaku Maths. Elementer av en polygon og dens klassifisering. Gjenopprettet fra: sangakoo.com.
4. Wikipedia. Pentadecágono. Gjenopprettet fra: er.Wikipedia.org.
5. Wolfram Math World. Pentadecagon. Gjenopprettet fra: Mathworld.Wolfram.com.