Mekanisk kraft hva er, applikasjoner, eksempler

De Mekanisk kraft Det er rytmen som arbeidet gjøres, som kommer til uttrykk på en matematisk måte for mengden arbeid utført per tidsenhet. Og siden arbeidet utføres på bekostning av absorbert energi, kan det også heves som energi per tidsenhet.

Ringer P til makt, W å jobbe, OG til energi og t Samtidig kan alt det ovennevnte oppsummeres i enkelt håndtering av matematiske uttrykk:

Figur 1. Gossamer Albatross, "Flying Bicycle", krysset kanalen til La Mancha på slutten av 1970 -tallet, og brukte bare menneskelig makt. Kilde: Wikimedia Commons. Gossamer Albatross. Guroadrunner på engelsk Wikipedia [Public Domain]

O vel:

Kraftenhetene i det internasjonale systemet (SI), som er systemet med universelt adopterte enheter, er Joule/Second eller Watt, som er forkortet w. Det ble således navngitt til ære for den skotske ingeniøren James Watt (1736-1819), kjent for å ha laget dampmotoren med en kondensator, oppfinnelse som begynte den industrielle revolusjonen.

Andre kraftenheter som brukes i bransjer er HP (Hestekraft eller krafthest) og CV (Steam Horse). Opprinnelsen til disse enhetene stammer også tilbake til James Watt og den industrielle revolusjonen, da målemønsteret var rytmen som en hest mot arbeid.

Både HP og CVen tilsvarer omtrent ¾ kilo-w som fremdeles brukes mye, spesielt i maskinteknikk, for eksempel i betegnelsen på motorer.

Watt-multipler, som de nevnte kilo-w = 1000 W brukes også ofte i strøm. Det er fordi Joule er en relativt liten energienhet. Det britiske systemet bruker libra-pie/sekund.

[TOC]

Hva er industri- og energiapplikasjoner

Kraftkonseptet er aktuelt for alle typer energi, enten det er mekanisk, elektrisk, kjemisk, vind, sononisk eller noe slag. Tid er veldig viktig i bransjen, fordi prosessene må utføres så raskt som mulig.

Enhver motor vil gjøre det nødvendige arbeidet for å ha nok tid, men det viktige er å gjøre det på kortest mulig tid, for å øke effektiviteten.

En veldig enkel applikasjon beskrives umiddelbart for å avklare skillet mellom arbeid og kraft godt.

Anta at et tungt objekt blir stoppet av et tau. For å gjøre det kreves det en ekstern agent som gjør det nødvendige arbeidet. La oss si at dette agenten overfører 90 J energi til objekt-kroppssystemet, slik at det settes i gang i 10 sekunder.

Kan tjene deg: tverrbølge

I dette tilfellet er energioverføringshastigheten 90 J/10 s eller 9 J/s. Da kan vi bekrefte at dette middelet, en person eller en motor har en 9 W utgangseffekt.

Hvis et annet eksternt middel er i stand til å oppnå samme forskyvning, enten på kortere tid eller overføre mindre energi, er det i stand til å utvikle større kraft.

Et annet eksempel: Anta at en energioverføring på 90 J, som klarer å flytte systemet i 4 sekunder. Utgangseffekten vil være 22.5 w.

Maskinytelse

Kraften er nært beslektet med ytelse. Energien som leveres til en maskin blir aldri fullstendig forvandlet til nyttig arbeid. En viktig del blir vanligvis spredt i varmen, noe som avhenger av mange faktorer, for eksempel maskindesign.

Det er derfor det er viktig å kjenne ytelsen til maskinene, som er definert som forholdet mellom det leverte arbeidet og energien som leveres:

η = arbeid levert av maskinen/energien som leveres

Hvor de greske tekstene η Angir ytelsen, et ekstra beløp som alltid er mindre enn 1. Hvis du også multipliserer med 100, har du ytelsen i prosentvis vilkår.

Eksempler

- Mennesker og dyr utvikler kraft under bevegelse. For eksempel, når du klatrer opp trapper, er det nødvendig å gjøre arbeid mot tyngdekraften. Sammenligning av to personer som går opp en stige, som går opp alle trinn først, vil ha utviklet mer kraft enn den andre, men begge gjorde den samme jobben.

- Apparater og maskiner er spesifisert deres utgangseffekt. En passende glødende pære for å belyse et rombrønn har en kraft på 100 W. Dette betyr at pæren forvandler strøm til lys og varme (de fleste) med en hastighet på 100 J/s.

- Motoren til en beskjæring av gress kan konsumere omtrent 250 W, og en bil er i størrelsesorden 70 kW.

- En hjemmelaget vannpumpeforsyning vanligvis 0.5 hk.

- Solen genererer 3.6 x 10 ²⁶ W strøm.

Kraft og hastighet

Øyeblikkelig kraft oppnås ved å ta en uendelig tid: P = Dw/dt. Kraften produsert av det forårsakende arbeidet med den lille uendelige forskyvningen dx er F (begge er vektorer), derfor DW = F ● dx. Erstatte alt i uttrykket for makt, gjenstår:

Kan tjene deg: sentrifugal kraft: Formler, hvordan den beregnes, eksempler, øvelser

Derfor kan strøm også uttrykkes som skalarproduktet mellom kraft og hastighet.

Menneskelig kraft

Folk er i stand til å generere krefter på rundt 1500 W eller 2 hestekrefter, i det minste for en kort periode, for eksempel å veie vekter.

I gjennomsnitt er den daglige effektutgangen (8 timer) 0.1 hk per person. Hvorav mye oversettes til varme, mer eller mindre samme mengde generert av en glødpære av 75 w.

En idrettsutøver i trening kan generere i gjennomsnitt 0.5 hk tilsvarer omtrent 350 J/s, ved å transformere kjemisk energi (glukose og fett) til mekanisk energi.

Figur 2. En idrettsutøver utvikler en gjennomsnittlig kraft på 2 hk. Kilde: Pixabay.

Når det gjelder menneskelig kraft, er det vanligvis å foretrekke. Den nødvendige ekvivalensen er:

1 kilokaloria = 1 Ernæringskalorie = 4186 J

En kraft på 0.5 hk høres ut som en veldig liten mengde, og det er for mange applikasjoner.

I 1979 ble det imidlertid opprettet en sykkel som ble drevet av mennesker som kunne fly. Paul MacCready designet Gossamer Albatross, Det krysset La Mancha -kanalen som genererte 190 W gjennomsnittlig utgang (figur 1).

Distribusjon av elektrisk energi

En viktig applikasjon er fordelingen av strøm blant brukere. Bedrifter som leverer elektrisitetsregninger energien som konsumeres, ikke den hastigheten den konsumeres. Det er grunnen til at de som leser regningen nøye, vil finne en veldig spesifikk enhet: Kilowatt-Hora eller KW-H.

Når navnet på Watt er inkludert i denne enheten, refererer imidlertid til energi og ikke strømmen.

Kilowatt-Hora brukes til å indikere forbruket av strøm, siden joule, som nevnt før, er en ganske liten enhet: 1 watt-hora eller w-h Det er arbeidet som er utført på 1 time gjennom en kraft på 1 watt.

Derfor 1 kw-h Det er arbeidet som gjøres på en time og arbeider med en kraft på 1 kW eller 1000 w. La oss sette tallene for å gi disse beløpene til Joules:

1 w-h = 1 w x 3600 s = 3600 j

1 kW-H = 1000 W x 3600 S = 3.6 x 10 ⁶ J

Det anslås at i et hjem kan rundt 200 kW-hora konsumeres per måned.

Det kan tjene deg: absolutt trykk: formel, hvordan det beregnes, eksempler, øvelser

Øvelser

Oppgave 1

En bonde bruker en traktor for å trekke en høypaca på M = 150 kg på et 15 ° skrå fly og ta den til låven, med konstant hastighet på 5.0 km / t. Korisk friksjonskoeffisient mellom høyfardo og rampen er 0.Fire fem. Finn traktorutgangskraften.

Løsning

For dette problemet er det nødvendig å tegne et fritt kroppsdiagram for Hay Fardo som går opp på det skrå planet. Være F Kraften som bruker traktoren til å klatre opp Bundo, α = 15º er hellingsvinkelen.

I tillegg er den kinetiske friksjonskraften involvert F_{ta på} som motsetter seg bevegelsen, pluss det normale N og vekten W (Ikke forveksle W av vekt med arbeid).

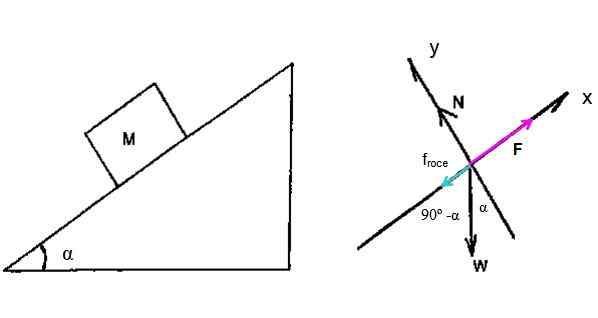Figur 3. Heo Fardo isolert kroppsdiagram. Kilde: f. Zapata.

Newtons andre lov tilbyr følgende ligninger:

∑ fx = f -w_x -F_{ta på} = 0 (Siden Bundo stiger i konstant hastighet)

∑fy = n - w_og = 0 (Det er ingen bevegelse langs X -aksen)

Den kinetiske friksjonen beregnes av:

F_{ta på} = Kinetisk friksjonskoeffisient x størrelse på normalen

F_{ta på} = 0.Fire fem . Wy = 0.45 x 150 kg x9.8 m/s2 x cos 15º = 639 n

F = w_x + F_{ta på} = M.g. sin α = 150 kg. 9.8 m/s² . sin 15 º + 639 n =  1019.42 n

Hastighet og styrke har samme retning og mening, derfor:

P = F ● v = F. v

Det er påkrevd å transformere hastighetsenhetene:

v = 5.0 km/ h = 1.39 m/ s

Erstatte verdier, får du endelig:

P = 1019.42 n x 1.39 m/ s = 1417 W = 1.4 kW

Oppgave 2

Motoren vist på figuren vil laste opp 2 kg -blokken, med start fra hvile, med en akselerasjon på 2 m/s² Og på 2 sekunder.

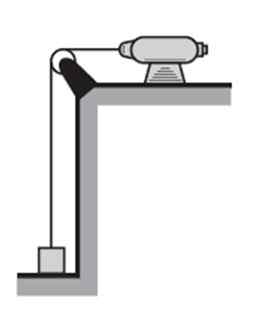Figur 4. En motor løfter et objekt til en viss høyde, som det er nødvendig å gjøre arbeid og utvikle strøm. Kilde: f. Zapata.

Regne ut:

a) Høyden nådd med blokken på den tiden.

b) Kraften som motoren må utvikle for å oppnå den.

Løsning

a) Det er en jevn variert rettlinjet bevegelse, derfor vil de tilsvarende ligningene bli brukt, med initial hastighet 0. Høyden nådd er gitt av:

y = ½ på² = ½ . 2 m/s² . (2 s)² = 4 m.

b) For å finne kraften som er utviklet av motoren, kan ligningen brukes:

P = ΔM/Δt

Og siden kraften som utøves på blokken er gjennom spenningen i tauet, som er konstant i størrelsesorden:

P = (MA).og/ΔT = 2 kg x 2 m/s² x 4 m / 2 s = 8 w

Referanser

1. Figueroa, d. (2005). Serier: Fysikk for vitenskap og ingeniørfag. Volum 2. Dynamisk. Redigert av Douglas Figueroa (USB).
2. Knight, r.  2017. Fysikk for forskere og ingeniørfag: En strategitilnærming.  Pearson.
3. FYSIKK LIBRETTEXTS. Makt. Gjenopprettet fra: Phys.Librettexts.org
4. Fysikkens hypertekstbok. Makt. Gjenopprettet fra: Fysikk.Info.
5. Arbeid, energi og kraft. Gjenopprettet fra: ncert.Nic.i