Relativ trykkformel, hvordan den beregnes, eksempler, trening

De Presirelativ Ón Det er det som måles med hensyn til en viss verdi eller Datum, som vanligvis er atmosfærisk trykk ved havnivå (standard atmosfæretrykk). Dette er aktuelt fordi en stor del av trykkmålingene blir utført under de gassformige lagene som utgjør atmosfæren, som utøver sitt eget press.

På den annen side måles det absolutte trykket med hensyn til et totalt vakuum, der det ikke er noen molekyler som samhandler. I en beholder der vakuumet er laget, er det ingen partikler som virker fra innsiden på veggene eller på gjenstander i det.

Figur 1. For å måle det relative trykket brukes en trykkmåler slik. Kilde: Wikimedia Commons.

Trykket som måles kan være over eller under atmosfæretrykk. I det første tilfellet er det snakk om måle trykk Og i den andre av vakuumtrykk.

Normalt er trykket som måles daglig i dekk og blodtrykk, relativt trykk, mens når atmosfæretrykket måles med et barometer, er det et absolutt trykk.

[TOC]

Relativ trykkformel

Det relative trykket er forskjellen mellom det absolutte trykket P_Abs og atmosfærisk trykk s_ATM, Det er et differensielt trykk eller forskjell i trykk. Ved det relative trykket P_Rel Det er kjent på engelsk som Måle trykk P_g Og det er gitt av forholdet:

P_Abs = S_ATM + P_g

P_Rel = S_Abs - P_ATM

For trykk brukes Pascal som en måleenhet for det internasjonale systemet med enheter, uavhengig av om det er et absolutt trykk eller et relativt trykk.

Pascal tilsvarer styrken som utøves av 1 Newton over et område på 1 m², Men andre enheter brukes ofte, for eksempel kvikksølv, vann, anglo -Saxon -enheter som som psi og andre.

Kan tjene deg: de 31 typene kraft i fysikk og deres egenskaper

Hvordan beregnes det relative trykket?

Hvis absolutt trykk er kjent på et punkt og standard atmosfæretrykk, er det relative trykket subtraksjonen mellom begge.

Anta for eksempel at det absolutte trykket i et visst system er 305 kPa. Å vite at standard atmosfæretrykk er 101.3 kPa, det relative trykket er:

P_g = S_Abs - P_ATM = 305 - 101.3 kPa = 203.7 kPa

KPA eller Kilopascal er tusen ganger større enn en Pascal. Det brukes oftere, siden trykkverdiene er i størrelsesorden tusenvis av Pascal. Vekten av et eple er omtrent 1 Newton og en Pascional tilsvarer denne kraften fordelt på en 1 meter sidevirksomhet. Andre multipler som Megapascal (1 MPa = 1 x 10⁶ Pa) eller Gigapascal (1 GPA = 1x 10⁹ Pa).

Trykket til eksemplet er manometrisk, fordi det er over atmosfæretrykket, men det er absolutt trykk under dette. For eksempel, hvis en gass i en beholder har et absolutt trykk på 50 kPa, er dens relative trykk et vakuumtrykk som gir sug:

P_g = S_Abs - P_ATM = 50 - 101.3 kPa = -51.3 kPa

I disse eksemplene ble standard atmosfæretrykket brukt, som er trykket ved havnivå. Men hvis det kreves mer nøyaktighet i beregningen, kan lokalt atmosfæretrykk brukes, noe som kan avvike fra 101.3 kPa, siden det avhenger av høyde og andre geografiske forhold.

I tekstene er vanligvis presset som er gitt relativt, og hvis det er pålagt å jobbe med absolutt press, skilles disse ut med bruk av abonnement for å unngå forvirring.

Kan tjene deg: sol

Variasjon av trykk med dybde

På hvert punkt inne i en væske som vann er det trykk. Forutsatt at vannet er inkomprimerbart, så dets tetthet forblir konstant og trykket varierer vertikalt.

Det kan sjekkes ved å ta en liten del av væsken i form av en tykk disk Dy det er i ro midt i flytende masse.

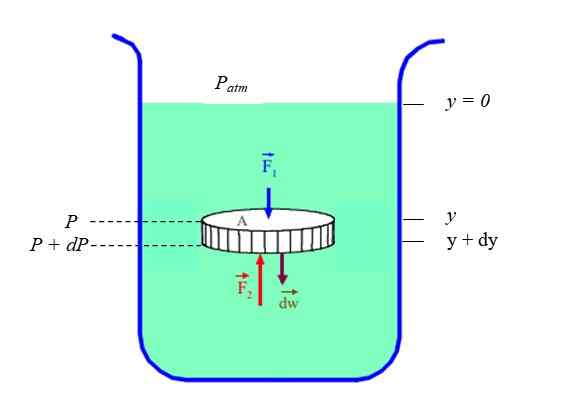Figur 2. En liten del av disk -formet væske, i statisk likevekt. Kilde: f. Zapata.

Kreftene på de sirkulære kantene på disken blir kansellert av jevnaldrende, men ikke kreftene som utøves av massen av væske over og under skiven: F₁ og F₂. I tillegg er det nødvendig å vurdere vekten av væskeskivenW I Newtons andre lov:

∑f_og = F₂ - F₁ - W = 0

Disse kreftene kan uttrykkes i forhold til trykket, som er den vinkelrett kraften per enhet av areal. På denne måten har vi presset P, produsert med kraft f₁:

F₁ = S. TIL

Hvor a er det sirkulære området på platen. På samme måte:

F₂ = (P + DP). TIL

Med P + DP trykket på dybden og + dy. Vekten er DW = DM . G:

(P + DP). A - s. A - DM . G = 0

Væsketettheten er ρ = dm/ dv, med DV volumet på væskeskiven, gitt av en.Dy. Denne måten:

(P + DP). A - s. A - ρa.Dy .G = 0

Ligningen som er oppnådd er forenklet til:

Dp - ρgdy = 0 → dp = ρgdy

Integrere begge sider fra og₁ opp til y₂:

= S₂ - P₁ = ρg (og₂ - og₁)

Begrepet s₂ - P₁ Det er en forskjell i trykk eller differensialtrykk. Hvis vi vil vite presset på det vertikale koordinatpunktet, og vi gjør det og₁ = 0, og₂ = y og P_enten = S_ATM. Med dette vil vi ha trykket i forhold til denne dybden, som utelukkende avhenger av dybde og:

Kan tjene deg: Uregelmessig galakse: Dannelse, egenskaper, typer, eksempler

P₂ - P_ATM = ρgy ⇒ s_Rel = ρgy

Eksempler på relativt trykk

Trykk i bunnen av et basseng

Vi har alle opplevd presset som kjennes ved å fordype oss i et basseng eller i havet. Hva er det relative trykket som merkes ved å bli nedsenket i et basseng med ferskvann på 5 meter dyp? Ved å bruke det forrige uttrykket, og vite at tettheten av ferskvann er 1000 kg/m³, Med G = 9.81 m/s² Det relative trykket er:

P_Rel = ρgy = 1000 x 9.81 x 5 PA = 49050 PA.

Press på et dekk

Kjøretøydekk har vanligvis et trykk på 32 psi. Dette er et relativt eller manometrisk trykk i pund per kvadrat tomme, enheten som brukes i engelsktalende land. Mange manometre er kalibrert i disse enhetene. 32 PSI tilsvarer 220632 PA O 220 KPA.

Trening løst

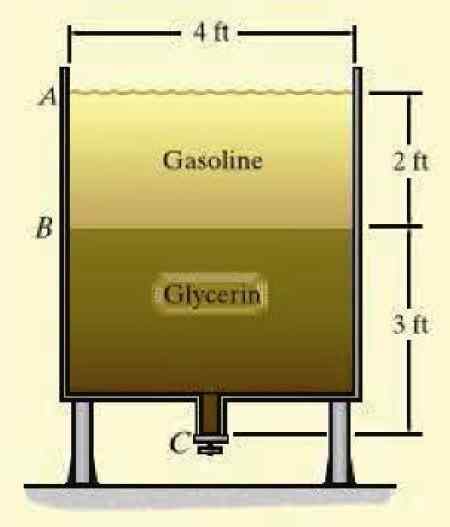
En tank inneholder bensin og glyserin, to ikke -muisible væsker (ikke bland) i de angitte høydene. Hva er det manometriske trykket i bunnen av tanken? De spesifikke vektene er festet, betegnet med den greske bokstaven γ, av hver væske:

γ_gass = 45.3 lb/ft³

γ_Gly = 78.7 lb/ft³

Figur 3. En tank full med to ikke -muskbare væsker. Kilde: Hibbeler, R. Væskemekanikk.

Løsning

Den spesifikke vekten γ av en væske er produktet av dens tetthet på grunn av akselerasjonen av tyngdekraften, derfor kan ligningen av det relative trykket uttrykkes som følger:

P_Rel = γ.og

Det relative trykket i bunnen av tanken skyldes både vekten av glyserin -kolonnen og den for bensin og er uavhengig av formen til tanken:

P_Rel = γ_gass . og_AB + γ_Gly . og_BC = (45.3 x 2 + 78.7 x 3) lb/ft² = 326.7 lb/ft²

Referanser

1. Cimbala, ca. 2006. Mekanikk av væsker, grunnleggende og applikasjoner. MC. Graw Hill.
2. Hibbeler, R. 2015. Væskemekanikk. 1. Ed. Pearson.
3. Mott, r.  2006. Væskemekanikk. 4. plass. Utgave. Pearson Education.
4. Sitter, a. 2006. Fluid Mechanics, en fysisk introduksjon. Alpha Omega.
5. Streeter, v. 1999. Væskemekanikk. McGraw Hill.
6. Zapata, f. Trykk og dybde. Gjenopprettet fra: Francesphysics.Blogspot.com.