Archimedes prinsippformel, demonstrasjon, applikasjoner

Han Archimedes 'prinsipp Han sier at et totalt eller delvis nedsenket kropp får en vertikal kraft som kalles trykk, som tilsvarer vekten av volumet av væske som er forskjøvet av kroppen. 

Noen gjenstander flyter i vannet, andre synker og noen delvis fordyper seg. For å synke en strandball er det nødvendig å gjøre en innsats, fordi den styrken umiddelbart blir oppfattet som prøver å returnere den til overflaten. I stedet synker en metallkule raskt. 

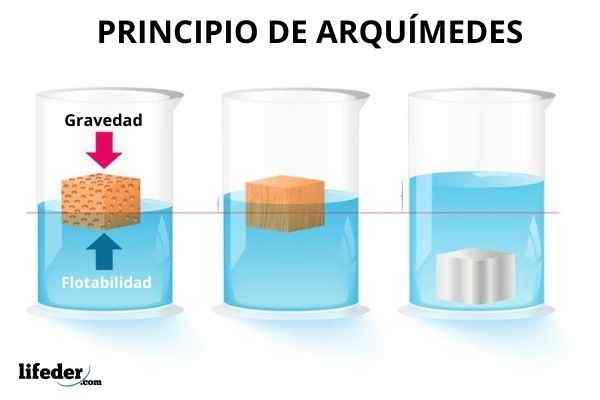
På den annen side virker nedsenkede gjenstander lettere, derfor er det en kraft som utøves av væsken som er imot vekt. Men du kan ikke alltid kompensere i det hele tatt til tyngdekraften. Og selv om det er tydeligere med vann, er gasser også i stand til å produsere denne kraften på de nedsenkede gjenstandene i dem.

[TOC]

Historie

Archimedes of Syracuse (287-212 A. C.) Det var den som må ha oppdaget dette prinsippet, og var en av de største forskerne i historien. De sier at King Hierón II av Syracuse sendte en gullsmed for å produsere en ny krone, som han ga ham en viss mengde gull.

Archimedes

Da kongen mottok den nye kronen, hadde han riktig vekt, men han mistenkte at gullsmeden hadde jukset ham ved å tilsette sølv i stedet for gull. Hvordan kunne jeg sjekke det uten å ødelegge kronen?

Hierón kalte Archimedes, hvis berømmelse av lærde var godt kjent, for å hjelpe ham med å løse problemet. Legenden bekrefter at Archimedes var fordypet i badekaret da han fant svaret, og slik var hans følelser, at han løp naken gjennom gatene i Syracuse for å lete etter kongen som skrek "Eureka", som betyr "jeg fant det".

https: // giphy.com/gifs/stito3echtlnbvliz3

Hva fant Archimedes? Vel, når du tar et bad, vannstanden i badekaret, da han kom inn, noe som betyr at en nedsenket kropp fortrenger et visst volum av væske.

Og hvis jeg senket kronen i vann, måtte den også bevege et visst volum av vann hvis kronen var laget av gull og en annen hvis den ble laget av legering med sølv.

Archimedes prinsippformel

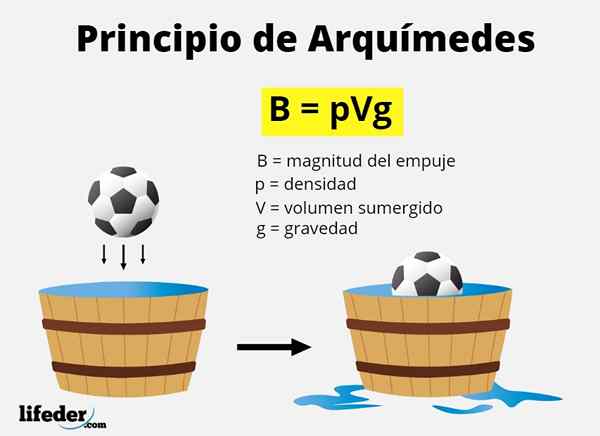
Salgsfremmende styrke det er referert til i Archimedes -prinsippet er kjent som trykk hydrostatisk enten Flotasjonsstyrke Og som vi har sagt, tilsvarer det volumet av væsken som er forskjøvet av kroppen når den er nedsenket.

Det fortrengte volumet tilsvarer volumet til objektet som er nedsenket, enten totalt eller delvis. Siden vekten av noe er mg, Og væskens masse er Tetthet x volum, Å benekte hvordan B til størrelsen på skyvekraften, matematisk må det:

B = m_flytende x g = væsketetthet x nedsenket volum x tyngdekraft

B = ρ_flytende x v_nedsenket x g

Der det greske bokstaven ρ ("Rho") betegner tettheten.

Den tilsynelatende vekten

Vekten av objektene beregnes av det velkjente uttrykket mg, Imidlertid føles ting lettere når de er nedsenket i vannet. 

Han tilsynelatende vekt Av et objekt er det som har når det er nedsenket i vann eller annen væske og å vite det, kan du få volumet til et uregelmessig objekt som kronen til King Hierón, som det vil bli sett nedenfor nedenfor.

Kan tjene deg: 13 eksempler på Newtons første lov i det virkelige liv

For å gjøre dette er det fullstendig nedsenket i vann og utsatt for et tau festet til en Dynamometer -et instrument utstyrt med en fjær som tjener til å måle krefter-. Jo større vekt på objekt.

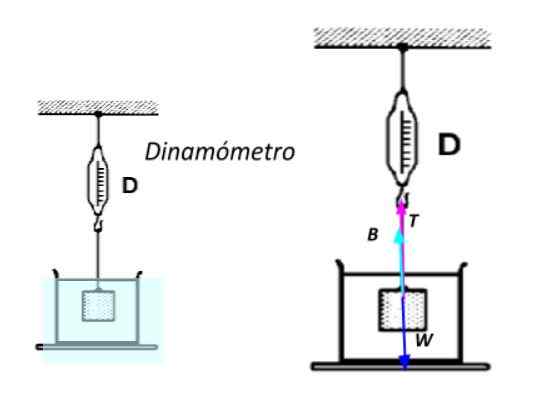Tilsynelatende vekt av et nedsenket objekt. Kilde: Utarbeidet av F. Zapata.

Bruke Newtons andre lov, vel vitende om at objektet er i ro:

Σf_og = B + t - w = 0

Den tilsynelatende vekten w_til Det tilsvarer spenning på T -tauet:

T = w_til

W_til = mg - ρ_flytende . V. g

Hvis det nedsenkede volum V er nødvendig, blir det fjernet som:

V = (w - w_til ) / ρ_flytende  . g

Demonstrasjon

https: // giphy.com/gifs/mcphppgtnpbhl4cgaq

Når en kropp senker seg, er skyvekraften styrken som følge av alle kreftene som utøves på kroppen gjennom trykket forårsaket av den omkringliggende væsken:

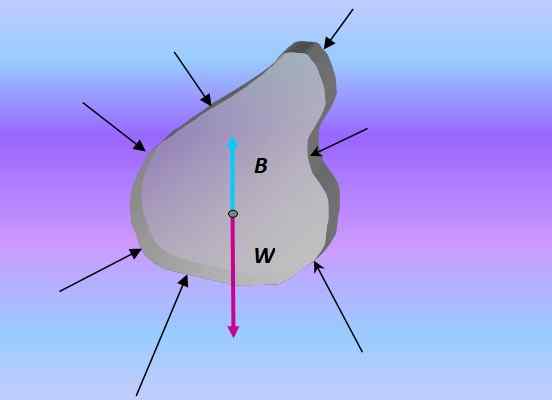Gratis kroppsdiagram over et nedsenket objekt. Kilde: Utarbeidet av F. Zapata.

Trykk og dybde

Siden trykket øker med dybden, er resultatet av disse kreftene alltid rettet vertikalt oppover. Derfor er Archimedes -prinsippet en konsekvens av det grunnleggende teoremet til det hydrostatiske, som relaterer trykket P utøvd av en væske med dybden z som:

P = ρ.g.z

Krefter på en statisk likevektsvæske

For å demonstrere Archimedes -prinsippet, tas en liten sylindrisk hvileporsjon i ro for å analysere kreftene som utøves på den, som vist i følgende figur. Kreftene på den buede overflaten av sylinderen blir kansellert med hverandre. 

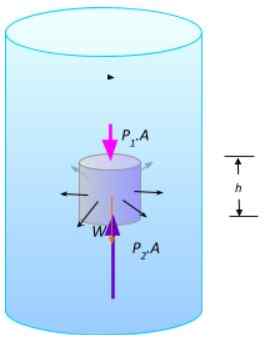En del av væske i likevekt. Kilde: Utarbeidet av F. Zapata.

Størrelsene til de vertikale kreftene er F₁ = P₁.A og F₂ = P2.A, det er vekten W. Ettersom væsken er i balanse, må summen av kreftene avlyses:

∑f_og = S₂.A- s₁.A- W = 0

P₂.A- s₁.A = w

Siden skyvekraften kompenserer til vekt, siden væskedelen er i ro, så:

B = s₂.A- s₁.A = w

Fra dette uttrykket følger det at skyvekraften skyldes forskjellen i trykk mellom sylinderens øvre ansikt og den nedre. Som W = mg = ρflytende. V. g, Du må:

B = ρ_flytende. V_nedsenket. g

Som nettopp er uttrykket for skyvekraften som er nevnt i forrige seksjon.

Archimedes Principle Applications

Ballonger som flyter: Archimedes -prinsippet i aksjon

Archimedes -prinsippet vises i mange praktiske anvendelser, blant dem vi kan navngi:

- Den aerostatiske ballongen. Som ved å ha en gjennomsnittlig tetthet mindre enn den omkringliggende luften, flyter i den på grunn av skyvekraften.

- Skipene. Skipets hjelm er tyngre enn vann. Men hvis skroget blir vurdert pluss luften inni, er kvotienten mellom den totale massen og volumet mindre enn vannet, og det er grunnen til at skipene flyter.

- Livet vester. Når de er bygget av lette og porøse materialer, er de i stand til å flyte fordi massevolumforholdet er mindre enn vannet.

- Den flytende for å lukke fyllekranen på en vanntank. Det er en sfære full av stort volumluft som flyter over vannet, som forårsaker skyvekraften - multiplisert med spakens effekt - lukker hetten på fylling av en vanntank når den har nådd nivået totalt.

Det kan tjene deg: Unidimensjonale bølger: Matematisk uttrykk og eksempler

Eksempler

Eksempel 1

Legenden forteller at King Hierón ga gullsmeden en viss mengde gull for å lage en krone, men den mistrolige monarken trodde at gullsmeden kunne ha lurt når han plasserte et mindre verdifullt metall inne i kronen enn kronen. Men hvordan kunne jeg vite uten å ødelegge kronen? 

Kongen bestilte Archimedes og dette, på jakt etter løsningen, oppdaget hans berømte prinsipp.

Anta at kronen veier 2,10 kg-f i luften og 1,95 kg-f når den er helt nedsenket i vann. I dette tilfellet er det ingen bedrag?

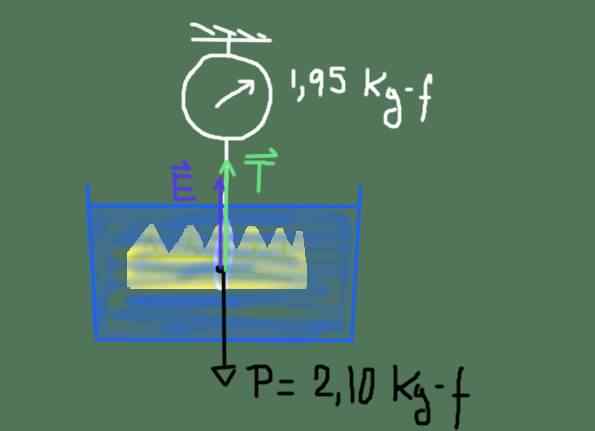King Herons Crown Free Body Diagram. Kilde: Utarbeidet av F. Zapata

Krefter -diagrammet er vist i forrige figur. Disse kreftene er: vekten P av kronen, skyvekraften OG og spenningen T av tauet som henger fra skalaen.

P = 2,10 kg-f og t = 1,95 kg-f er kjent, det er nødvendig å bestemme størrelsen på skyvekraften OG:

T + e = p ⇒ e = p - t = (2,10 - 1,95) kg -f = 0,15 kg -f

På den annen side, i henhold til Archimedes -prinsippet, tilsvarer skyvekraften vekten av det utvidede vannet i plassen som er okkupert av kronen, det vil si tettheten av vannet med volumet av kronen på grunn av tyngdekraften :

E = ρ_vann⋅V⋅g = 1000 kg/m^3 ⋅ V ⋅ 9,8 m/s^2 = 0,15 kg ⋅ 9,8 m/s^2

Hvor kronvolumet kan beregnes:

V = 0,15 kg / 1000 kg / m^3 = 0,00015 m^3

Kronens tetthet er kvotienten mellom kronen på kronen ut av vannet og volumet av den:

Kronetetthet = 2,10 kg / 0,00015 m^3 = 14000 kg / m^3

Tettheten av rent gull kan bestemmes ved en lignende prosedyre, og resultatet er 19300 kg/m^3.

Sammenligning av de to tetthetene er det tydelig at kronen ikke er rent gull! 

Eksempel 2 

Basert på dataene og resultatet av eksempel 1, er det mulig å bestemme hvor mye gull som ble stjålet av gullsmeden i tilfelle at en del av gullet er erstattet av sølv, som har en tetthet på 10500 kg/m^3 3 3 3.

Vi vil kalle ρc til kronen til kronen, ρo til tettheten av gull og ρ_p til sølvtettheten.

Den totale massen av kronen er:

M = ρc⋅V = ρo⋅Vo + ρ_p⋅Vp

Det totale volumet av kronen er volumet av sølv pluss gullvolumet:

V = vo + vp ⇒ vp = v - vo

Erstatte i masselikningen:

ρc⋅V = ρo⋅vo + ρ_p⋅ (v - vo) ⇒ (ρo - ρ_p) Vo = (ρc - ρ_p) V

Det vil si at gullvolumet som inneholder kronen til totalt volum V er:

Vo = v⋅ (ρc - ρ_p)/(ρo - ρ_p) = ..

... = 0,00015 m^3 (14000 - 10500)/(19300 - 10500) = 0,0000596 m^3

For å vite vekten i gull som inneholder kronen, multipliserer vi VO for tettheten av gull:

Kan tjene deg: Høyre håndregel

MO = 19300 *0.00005966 = 1.1514 kg

Siden kronen på kronen er 2,10 kg, vet vi at 0,94858 kg gull ble stjålet av gullsmeden og erstattet av sølv.

Løste øvelser

Oppgave 1

En enorm heliumballong er i stand til å opprettholde i balanse (uten å gå opp eller gå ned) til en person.

Anta at vekten til personen, pluss kurven, strengene og ballongen er 70 kg. Hva er volumet av helium som er nødvendig for at dette skal skje? Hvilken størrelse vil ballongen ha?

Løsning

Vi vil anta at skyvekraften hovedsakelig produseres av volumet av helium og at skyvekraften til resten av komponentene er veldig liten sammenlignet med helium som opptar mye mer volum.

I dette tilfellet vil et heliumvolum være påkrevd i stand til å gi et 70 kg + vektstøt.

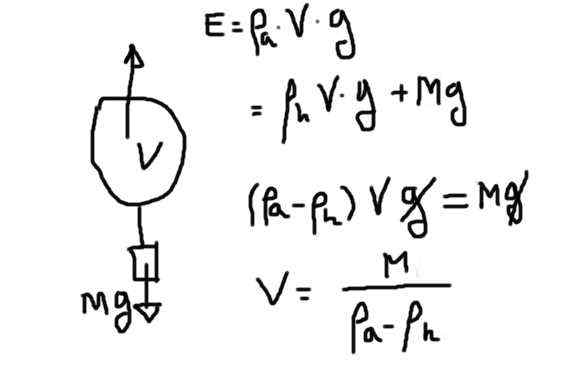Gratis kropp fdiaogram full av helium. Kilde: Utarbeidet av F. Zapata.

Skypen er produktet av heliumvolum på grunn av tettheten av helium på grunn av tyngdekraften. Den skyvekraften må kompensere for vekten på helium pluss resten av resten.

Da⋅v⋅g = da⋅v⋅g + m⋅g

der det konkluderer med at v = m / (da - dh)

V = 70 kg / (1.25 - 0,18) kg/m^3 = 65.4 m^3

Det vil si at 65 er påkrevd.4 m^3 av helium ved atmosfæretrykk for støtte.

Hvis vi antar en sfærisk ballong, kan vi finne radien til den samme fra forholdet mellom volumet og radiusen til en sfære:

V = (4/3) ⋅π⋅r^3

Hvor r = 2,49 m. Med andre ord vil det være nødvendig med en 5 m diameter full av helium.

Oppgave 2

Materialer med lavere tetthet som vann flyter i samme. Anta at du har polystyrenbiter (hvit kork), tre og is. Hans tettheter i kg per kubikkmåler er henholdsvis: 20, 450 og 915.

Finn hvilken brøkdel av det totale volumet som er ut av vannet, og hvilken høyde som skiller seg ut med hensyn til overflaten av vannet som tar som tetthet av sistnevnte 1000 kilo per kubikkmeter.

Løsning 

Flytbarhet oppstår når kroppsvekten er lik skyvekraften på grunn av vann:

E = m⋅g

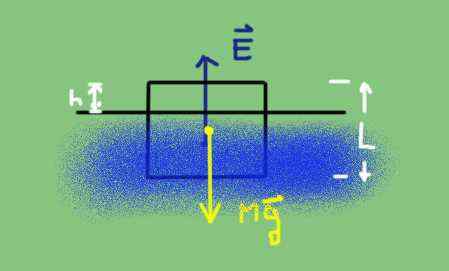Gratis kroppsdiagram over et delvis nedsenket objekt. Kilde: Utarbeidet av F. Zapata.

Vekt er kroppens tetthet DC multiplisert med volum V og ved akselerasjonen av tyngdekraften g.

Skypen er vekten av den fordrevne væsken i henhold til Archimedes -prinsippet og beregnes ved å multiplisere tettheten D av vannet med det nedsenkede volumet V 'og ved akselerasjonen av tyngdekraften.

Det er:

D⋅V'⋅g = dc⋅V⋅g

Noe som betyr at den nedsenkede volumfraksjonen er lik kvotienten mellom kroppstetthet og vanntetthet.

(V '/V) = (DC/D) 

Det vil si at den enestående volumfraksjonen (V "/V) er

(V "/V) = 1 - (DC/D)

Ja h Det er den enestående høyden og L Kubesiden Volumfraksjonen kan skrives som

(H⋅l^2)/(l^3) = h/l, Med andre ord, den enestående høydefraksjonen er også

(H/L) = 1 - (DC/D)

Da er resultatene for det forespurte materialet:

Polystyren (hvit kork):

(H/L) = (V "/V) = 1 - (DC/D) = 1- (20/1000) = 98% ut av vannet

Tre:

(H/L) = (V "/V) = 1 - (DC/D) = 1- (450/1000) = 55% ut av vannet

Is:

(H/L) = (V "/V) = 1 - (DC/D) = 1- (915/1000) = 8.5% ut av vannet

Referanser

1. Bauer, w. 2011. Fysikk for ingeniørfag og vitenskap. Volum 1. Mc Graw Hill. 417-455.
2. Cengel Y, Cimbala J. 2011.Væskemekanikk. Grunnleggende og applikasjoner. Første utgave. McGraw Hill.
3. Figueroa, d. (2005). Serier: Fysikk for vitenskap og ingeniørfag. Volum 4. Væsker og termodynamikk. Redigert av Douglas Figueroa (USB). 1 - 42.
4. Giles, r. 2010. Væske og hydraulisk mekanikk. McGraw Hill. 
5. Rex, a. 2011. Fundamentals of Physics. Pearson. 239-263.
6. Tippens, p. 2011. Fysikk: konsepter og applikasjoner. 7. utgave. McGraw Hill.