Pentagonal prismeegenskaper, deler, hjørner, kanter, volum

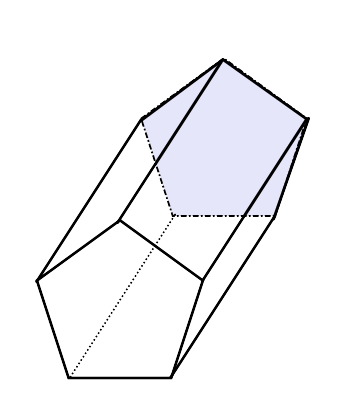
EN Femkantet prisme Det er en tre -dimensjonal geometrisk figur hvis baser, identisk, har en femkantform, og har også totalt 5 -sider i form av parallellogram.

Hvis ansiktene er rektangulære, sies det at det er en Rett femkantet prisme, Mens kantene er tilbøyelige til basene, er det en skrå femkantet prisme. I det følgende bildet er det et eksempel på hver.

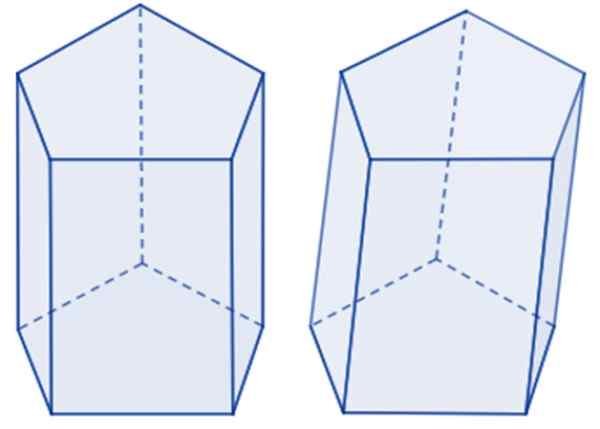Femkantet prisme til venstre og skrå til høyre. Kilde: Wikimedia Commons.

Basen Pentagon kan være regelmessig hvis fem sider har samme mål, så vel som indre vinkler, ellers er det en uregelmessig Pentagon. Hvis prismebasen er vanlig, handler det om Regelmessig femkantet prisme. Ellers er et prisme uregelmessig femkantet.

Uregelmessige base femkantede prismer som brukes i moderne konstruksjon. Kilde: Bakgrunnsbluss.

Pentagonal prisme er en harmonisk struktur som brukes i arkitektur og design av gjenstander, for eksempel den moderne bygningen vist i den øvre figuren. Uregelmessig Pentagons -formede vinduer danner basenes base.

[TOC]

Femkantet prismeegenskaper

-Det er en tre -dimensjonal geometrisk figur, overflatene som komponerer den inneholder et visst volum.

-Basene deres er pentagoner, og deres sideflater kan være rektangler eller parallellogrammer.

-Den har toppunktene -hjørnene på Prisma -og kanter -Bordene eller bredden-.

-Hvis kantene som forener basene er vinkelrett på dem, er prisme rett, og hvis de er tilbøyelige, er prisme skrå.

-Når basen er en femkant hvis indre vinkler er mindre enn 180 º, er prisme konveks, Men hvis en eller flere indre vinkler er større enn 180º, er det et prisme konkav.

Femkantet prismeelementer

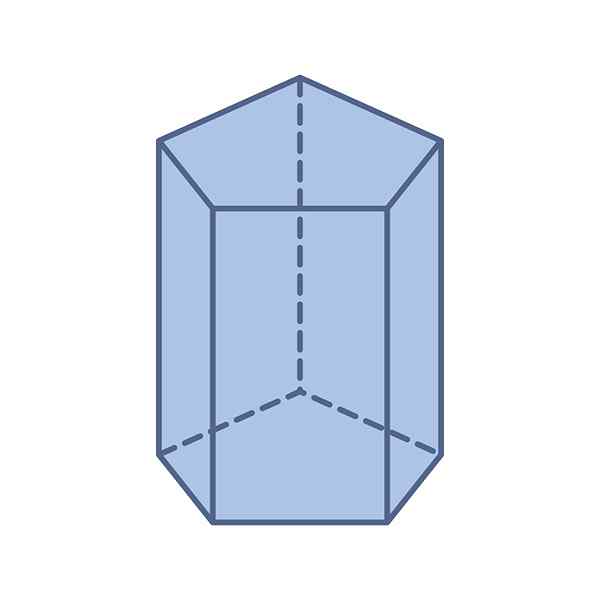
-Baser: Den har to femkantede og kongruente baser -målingene er de samme -enten regelmessige eller uregelmessige.

Kan tjene deg: Generell formel: kvadratiske ligninger, eksempler, øvelser

-Ansikter: Et femkantet prisme har totalt 7 ansikter: de to femkantede basene og de fem parallellogramene som utgjør sidene.

-Kant: segment som blir med to baser, vist i rødt i figur 3 eller den som blir med to sider.

-Høyde: Avstand mellom ansiktene. Hvis prisme er rett, sammenfaller denne avstanden med størrelsen på kanten.

-Toppunkt: vanlig punkt mellom en base og to sidesider.

Den nedre figuren viser en vanlig base femkantet prisme, der segmentene som danner basen har like mål, kalt til.

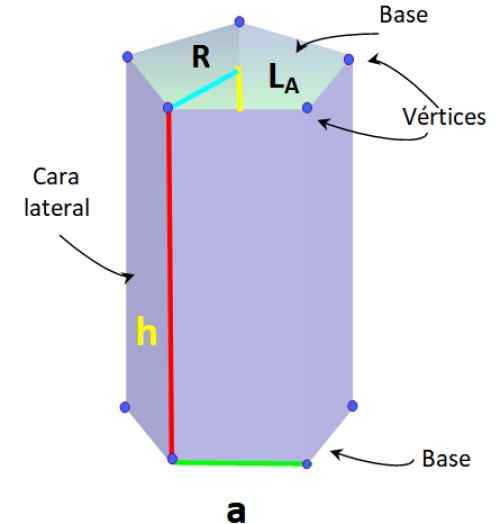 Vanlige femkantede prismeelementer. Kilde: f. Zapata.

Denne typen prisme har også følgende elementer, typisk for den vanlige Pentagon:

-Radio r: Avstand mellom midten av Pentagon og en av toppunktene.

-Apothem l_TIL: segment som blir med i sentrum med midtpunktet til en av sidene av Pentagon.

Hvor mange hjørner har et femkantet prisme har?

I en femkant er det 5 hjørner, og ettersom det femkantede prisme har to pentagoner som baser, har denne kroppen totalt 10 hjørner.

Hvor mange kanter har et femkantet prisme?

Du kan beregne antall kanter for geometriske kropper med flate ansikter, for eksempel prismer, ved hjelp av Euler Teorem For konvekse polyhedros. Leonhard Euler (1707-1783) er en av de største matematikerne og fysiske i historien.

Teoremet etablerer en sammenheng mellom antall ansikter, som vi vil kalle C, mengden av hjørner V og de totale kantene a som følger:

C+V = A+2

For det femkantede prisme har vi: C = 7 og V = 10. Rydding til antall kanter:

Det kan tjene deg: Bijjektive funksjon: Hva er det, hvordan gjøres det, eksempler, øvelser

A = C+V-2

Erstatte verdier:

A = 7 + 10 - 2 = 15

Et femkantet prisme har 15 kanter.

Hvordan få volumet av et femkantet prisme?

Volumet av det femkantede prisme måler plassen som er låst av sidene og basene. Det er et positivt beløp som beregnes av følgende egenskap:

Ethvert fly som skjærer til prisme vinkelrett på kantene, genererer et kryss på samme måte som basen, det vil si en femkant av de samme dimensjonene.

Derfor er volumet av det femkantede prisme et produkt av baseområdet og høyden på prisme.

Være TIL_B femkantet baseområde og h Prismens høyde, deretter volumet V er:

V = a_B x h

Denne formelen er generell, og er gyldig for ethvert prisme, enten regelmessig eller uregelmessig, rett eller skrå.

Volumet av et prisme kommer alltid i enheter av lengde høyt til kuben. Hvis lengden på sidene og høyden på prisme er gitt i meter, uttrykkes volumet i m³, at "kubikkmeters" blir lest. Andre enheter inkluderer CM³, km³, tommer³ og mer.

- Vanlig femkantet prismevolum

I Pentagonal Prism regelmessig er basene vanlige pentagoner, noe som betyr at siden og indre vinkler er de samme. Gitt kroppens symmetri, beregnes Pentagon -området og derfor volumet lett på flere måter:

Å kjenne høyden og måling av siden

Være til Målet på den femkantede basisiden. I så fall beregnes området av:

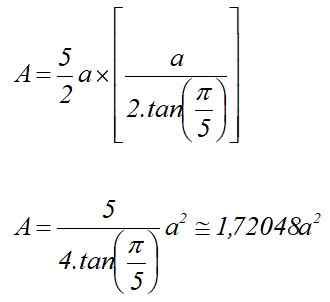
Derfor er volumet av det vanlige femkantede prisme av høyden H:

Kan tjene deg: imaginære tall: egenskaper, applikasjoner, eksempler

V = 1.72048 a²⋅ h

Å kjenne høyden og målet på radioen

Når Radio r Fra den femkantede basen kan denne andre ligningen brukes til baseområdet:

A = (5/2) r²⋅ Sen 72º

På denne måten er volumet av det femkantede prisme gitt av:

V = (5/2) r² ⋅ H ⋅ sen 72º

Hvor h Det er høyden på prisme

Å kjenne høyden, målet på apoteme og omkretsverdi

Pentagonal baseareal kan beregnes hvis det_TIL:

A = s. L_TIL / 2

Multiplisere dette uttrykket med høydenes verdi h, Vi har volumet av prisme:

V = P. L_TIL .H / 2

- Uregelmessig femkantet prismevolum

Formelen som er gitt i begynnelsen er til og med gyldig når basen av prisme er en uregelmessig femkant:

V = a_B x h

For å beregne basisområdet brukes forskjellige metoder, for eksempel:

-Trianguleringsmetode, som består av å dele Pentagon i trekanter og firkantede, hvis respektive områder lett blir beregnet. Pentagon -området vil være summen av områdene for disse enklere figurene.

-Gauss Determinants -metode, som du må kjenne til toppunktene på figuren.

Når verdien av området er bestemt, multipliseres det med høyden på prisme for å oppnå volumet.

Referanser

1. Alexander, d. 2013. Geometri. 5. plass. Utgave. Cengage Learning.
2. Matematikk åpen referanse. Polygonområde. Gjenopprettet fra: Mathpenref.com.
3. Universformler. Euler Teorem for Polyhedros. Gjenopprettet fra: Universoformulas.com.
4. Universformler. Område av en vanlig femkant. Gjenopprettet fra: Universoformulas.com.
5. Wikipedia. Prisme. Gjenopprettet fra: er.Wikipedia.com.
6. Wikipedia. Femkantet prisme. Gjenopprettet fra: er.Wikipedia.com.