Trapezoidal prisme

Hva er et trapesformet prisme?

EN Trapezoidal prisme Det er et prisme slik at de involverte polygonene er trapezoider. Definisjonen av prisme er et geometrisk legeme dannet av to like og parallelle polygoner med hverandre, og resten av ansiktene er parallellogrammer.

Et prisme kan ha forskjellige former, som ikke bare avhenger av antall sider av polygonen, men på selve polygonen.

Hvis polygonene i et prisme er firkantet, er dette for eksempel forskjellig fra et prisme som involverer rhombuses, til tross for at begge polygoner har samme antall sider. Derfor avhenger det av hva den firkantede involverte.

Kjennetegn på et trapesformet prisme

For å se egenskapene til et trapesformet prisme, bør du begynne med å vite hvordan det trekkes, så hvilke egenskaper basen oppfyller, hva er overflatenes område og til slutt hvordan volumet beregnes.

1. Tegne et trapesformet prisme

For å tegne det, er det først nødvendig å definere hva en trapes. En trapes er en uregelmessig polygon på fire sider (firkantet), men på en slik måte at den bare har to parallelle sider kalt baser og avstanden mellom basene kalles høyde.

For å tegne det rette trapezoidale prisme, begynner du å tegne en trapesoid. Deretter projiseres en vertikal linje med lengde "H" fra hver vertice, og til slutt trekkes en annen trapesformet at toppunktene sammenfaller med endene av de tidligere trukket linjene.

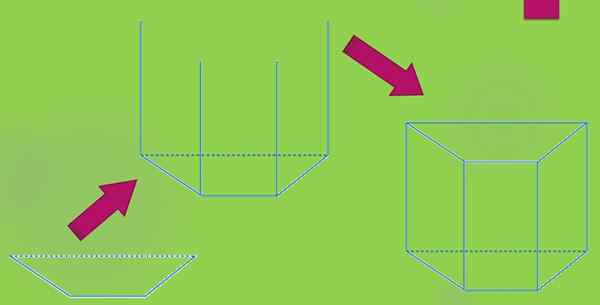
Du kan også ha skrå trapesformet prisme, hvis konstruksjon ligner den forrige, du må bare tegne de fire parallelle linjene med hverandre.

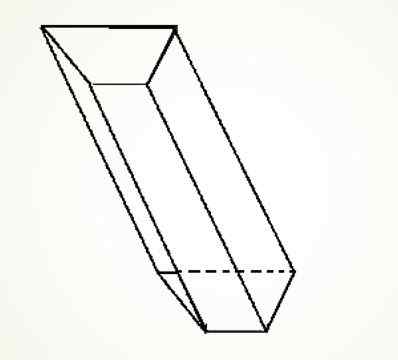
2. Egenskaper til en trapes

Som nevnt før, avhenger prismeformen av polygonen. I det spesielle tilfellet av trapesen kan vi finne tre forskjellige typer baser:

Rektangel trapes: Det er den trapes som en av sidene er vinkelrett på dens parallelle sider eller som ganske enkelt har en rett vinkel.

Trapezium isosceles: Det er en trapesoid som den ikke -parallelle sider har samme lengde på.

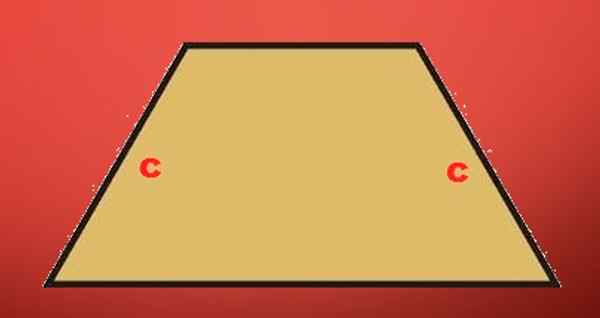
Escaleno Trapezio: Det er den trapesen som ikke er isosceles eller rektangel; Dens fire sider har forskjellige lengder.

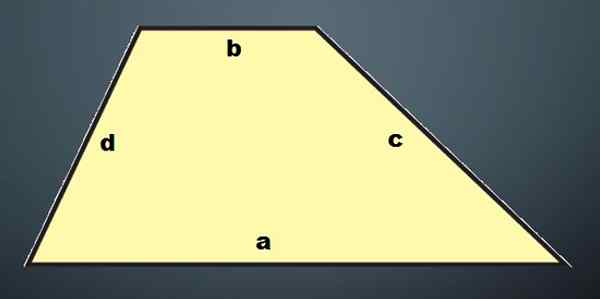
Som det fremgår av, i henhold til den type trapes som brukes, vil det oppnås et annet prisme.

3. Flateareal

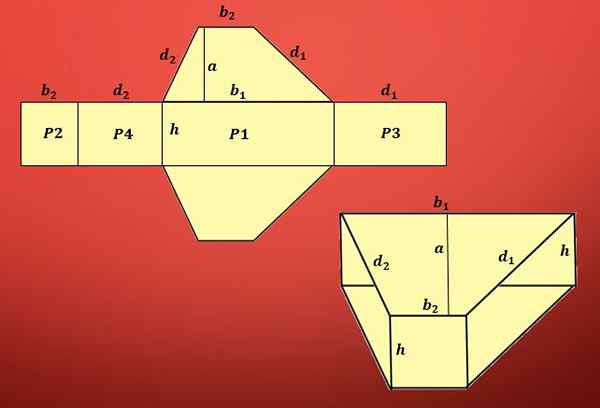
For å beregne området på overflaten til et trapesformet prisme, må vi kjenne området til trapesformet og området til hvert parallellogram involvert.

Som det kan sees på bildet, involverer området to trapeser og fire forskjellige parallelle.

Området til en trapes er definert som t = (b1+b2) xa/2 og områdene til parallellogrammer er p1 = hxb1, p2 = hxb2, p3 = hxd1 og p4 = hxd2, hvor “b1” og “b2 ”Er basene til trapesformet,” D1 "og" D2 ".

Derfor er området på overflaten til et trapesformet prisme A = 2T+P1+P2+P3+P4.

4. Volum

Siden volumet av et prisme er definert som V = (polygonområde) x (høyde), kan det konkluderes med at volumet til et trapesformet prisme er v = txh.

5. applikasjoner

Et av de vanligste gjenstandene som har form av et trapesformet prisme er en gullgull eller ramper som brukes i motorsykkelløp.