Frekvens sannsynlighetskonsept, hvordan beregnes og eksempler

De Frekvens sannsynlighet er En underdefinisjon innen studiet av sannsynlighet og dens fenomener. Studiemetoden med hensyn til hendelser og attributter, er basert på store mengder iterasjoner, og observerer dermed hver på lang sikt eller til og med uendelige repetisjoner.

For eksempel inneholder en gummitansk konvolutt 5 gummi i hver farge: blå, rød, grønn og gul. Du vil bestemme sannsynligheten for at hver farge må forlate etter et tilfeldig utvalg.

Kilde: Pexels

Det er kjedelig å forestille seg å få en gummi, ta opp den, returnere den, ta ut en gummi og gjenta det samme flere hundre eller flere tusen ganger. Du kan til og med ønske å observere oppførselen etter flere millioner iterasjoner.

Men tvert imot er det interessant å oppdage at etter få repetisjoner er den forventede sannsynligheten for 25% ikke fullt oppfylt, i det minste ikke for alle farger etter at 100 iterasjoner oppstår.

Under frekvenssannsynlighetsmetoden vil tildelingen av verdier bare være gjennom studiet av mange iterasjoner. På denne måten må prosessen gjennomføres og helst registreres på en datastyrt eller emulert måte.

Flere strømmer avviser frekvenssannsynlighet, og krangler mangel på empirisme og pålitelighet i tilfeldige kriterier.

[TOC]

Hvordan beregnes frekvens sannsynlighet?

Når du programmerer eksperimentet i et hvilket.

Det forrige eksemplet blir verdsatt fra frekvenstilnærmingen:

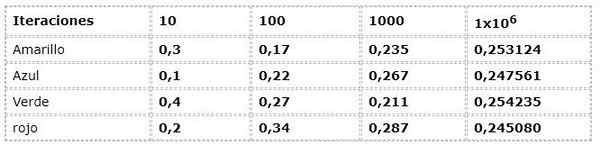
Numeriske data tilsvarer uttrykket:

N (a) = antall forekomster/ antall iterasjoner

Der n (a) representerer den relative hyppigheten av "a" -hendelsen

“A” tilhører settet med mulige resultater eller prøveområde ω

Det kan tjene deg: Multipler av 8: Hva er og forklaring

Ω: rød, grønn, blå, gul

Det er en betydelig spredning i de første iterasjonene, når frekvenser med opptil 30% av forskjeller blir observert med hverandre, noe som er et veldig høyt faktum for et eksperiment som teoretisk har hendelser med samme mulighet (utstyrbar).

Men når iterasjonene vokser, virker verdiene mer og mer for de som presenteres av den teoretiske og logiske strømmen.

Lov om de store tallene

Som en uventet avtale mellom teoretiske og frekvenstilnærminger, oppstår loven om stort antall. Der det er fastslått at etter en betydelig mengde iterasjoner, nærmer verdiene til frekvenseksperimentet teoretiske verdier.

I eksemplet kan du legge merke til hvordan verdier er tilnærmet til 0,250 når iterasjoner vokser. Dette fenomenet er elementært i konklusjonene fra mange sannsynlige verk.

Kilde: Pexels

Andre sannsynlighetsmetoder

Det er ytterligere 2 teorier eller tilnærminger til forestillingen om sannsynlighet i tillegg til Frekvens sannsynlighet.

Logisk teori

Din tilnærming er orientert mot fenomenets deduktive logikk. I forrige eksempel er sannsynligheten for å oppnå hver farge 25% lukket. Med andre ord.

Subjektiv teori

Det er basert på kunnskapen og tidligere oppfatninger som hver enkelt har om fenomenene og attributtene. Uttalelser som "Det regner alltid i Holy Week " De adlyder et mønster av lignende hendelser som har skjedd tidligere.

Historie

Begynnelsen av implementeringen er fra det nittende århundre, når jeg har sitert det i flere av arbeidet i Cambridge England. Men det var først på det tjuende århundre at 2 statistisk matematikk utviklet og formet Frekvens sannsynlighet.

Kan tjene deg: Polynomligninger

En av dem var Hans Reichenbach, som utvikler sitt arbeid i publikasjoner som "Theory of Probability" publisert i 1949.

Den andre var Richard von Mises, som utviklet arbeidet sitt grundigere gjennom flere publikasjoner og foreslo å anse sannsynlighet som en matematisk vitenskap. Dette konseptet var nytt i matematikk og ville markere begynnelsen på en tid med vekst i studiet av Frekvens sannsynlighet.

Egentlig utgjør denne hendelsen den eneste forskjellen med bidragene fra generasjonen av Venn, Counot og Helm. Hvor sannsynligheten blir et motstykke som geometri og mekanikk.

< La teoría de las probabilidades trata con massive fenomener og repeterende hendelser. Problemer der enten den samme hendelsen gjentas igjen og igjen, eller et stort antall ensartede elementer er involvert samtidig> Richard von Mises

Massive fenomener og repeterende hendelser

Tre typer kan klassifiseres:

• Fysikk: Obdosemønstre av naturen utover en tilfeldig tilstand. For eksempel oppførselen til molekylene til et element i en prøve.
• Sjanse: dens grunnleggende vurdering er tilfeldighet, som ved å gi ut en terning gjentatte ganger.
• Biologisk statistikk: Test emnevalg i henhold til deres egenskaper og attributter.

I teorien spiller individet som måler en rolle i de sannsynlige dataene, fordi det er hans kunnskap og opplevelser som formulerer denne verdien eller spådommen.

I Frekvens sannsynlighet Hendelser vil bli betraktet som samlinger som skal behandles, der individet ikke spiller noen rolle i anslaget.

Attributter

I hvert element oppstår det en attributt, som vil være variabel i henhold til arten av dette. For eksempel, i typen fysisk fenomen, vil vannmolekyler ha forskjellige hastigheter.

Det kan tjene deg: Triangulous likhetskriterier

I lanseringen av terningen kjenner vi prøveområdet ω som representerer attributtene til eksperimentet.

Ω: 1, 2, 3, 4, 5, 6

Det er andre attributter som ω_P  eller vær merkelig ω_Yo

Ω_p : 2, 4, 6

Ω_Yo : 1, 3, 5

Som kan defineres som ikke -elementære attributter.

Eksempel

• Du vil beregne hyppigheten av hver mulig sum i lanseringen av to terninger.

For dette er et eksperiment programmert der to tilfeldige verdier mellom [1, 6] legges til i hver iterasjon.

Dataene blir registrert i en tabell og trender i stort antall blir studert.

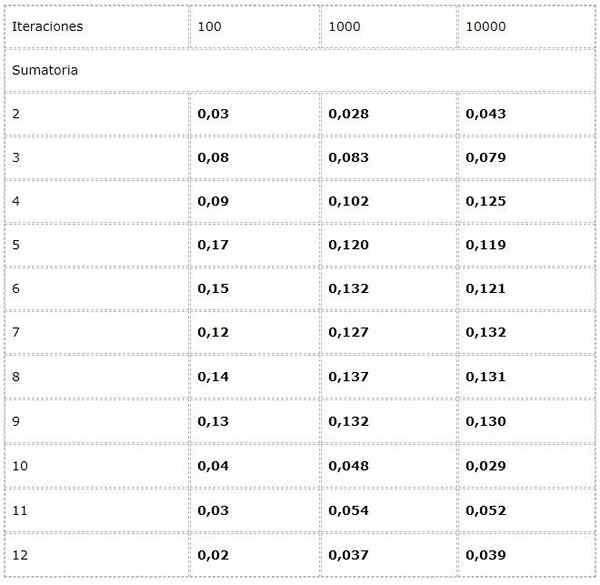
Det observeres at resultatene kan variere betydelig mellom iterasjoner. Imidlertid kan loven om store antall sees i den tilsynelatende konvergensen som er presentert i de to siste kolonnene.

Referanser

1. Statistikk og evaluering av bevis for rettsmedisinske forskere. Andre utgave. Colin G.G. Aitken. Matematikkskole. University of Edinburgh, Storbritannia
2. Matematikk for informatikk. Eric Lehman. Google Inc.
   F Thomson Leighton Department of Mathematics and the Computer Science and AI Laboratory, Massachussetts Institute of Technology; Akamai Technologies
3. Den aritmetiske læreren, bind 29. National Council of Teachers of Mathematics, 1981. Michigan University.
4. Lærings- og undervisningsnummerteori: Forskning i erkjennelse og instruksjon / redigert av Stephen R. Campbell og Rina Zazkis. Ablex Publishing 88 Post Road West, Westport CT 06881
5. Bernoulli, J. (1987). Ars conjectandi- 4ème partie. Rouen: Irem.