Kryssprodukt

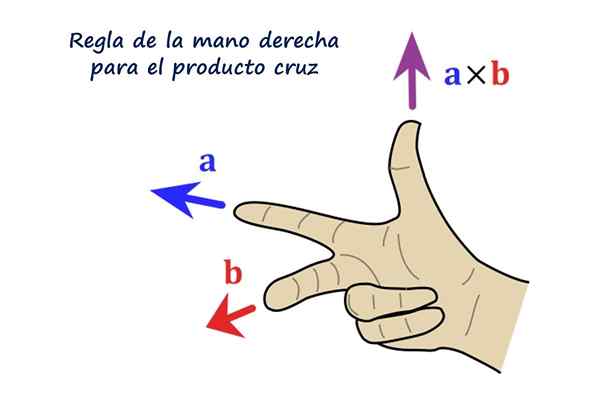
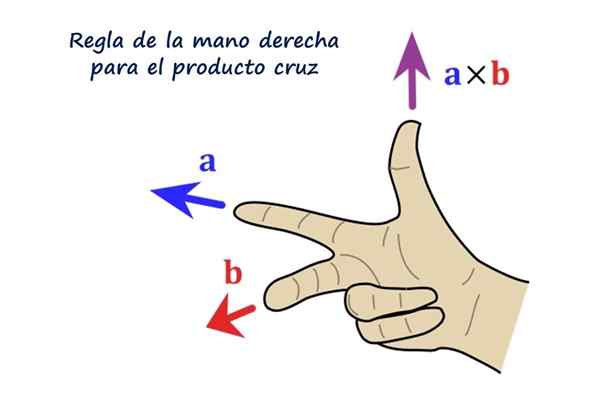Riktig regel for vektorproduktet. Kilde: f. Zapata.

Hva er kryssproduktet eller vektorproduktet?

Han Kryssprodukt, Også kalt vektorprodukt, det er en type produkt som utføres mellom to vektorer og resulterer i en annen vektor, vinkelrett på planet definert av de to første.

Kryssproduktet mellom to vektorer til og b, Det resulterer i en annen vektor R, Matematisk er skrevet som følger:

til × b = R

Det lyder slik: “En cruz b lik r ".

I trykt tekst er vektorer skrevet med dristige tekster, eller med en pil på bokstaven, for å skille dem fra størrelsesorden eller modulen. For dette brukes de, om hverandre, modulstenger og nåværende bokstaver, så den absolutte verdien av vektoren til Symbolet er skrevet slik:

│til│ = a

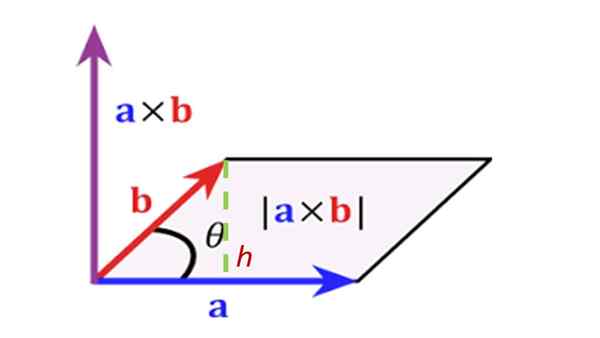
Den absolutte verdien eller modulen til vektorproduktet mellom to vektorer beregnes ved å multiplisere modulen til begge vektorene gjennom vinkelen θ mellom dem:

R = a ∙ b ∙ sen θ

Vektorenes retning R Det er vinkelrett på vektorene til og b. Følelsen av R Det er dextrogyr av til mot b Og i praksis bestemmes det ved å bruke regelen for høyre hånd, som består av å plassere indeksen, medium og tommelen på høyre hånd som følger:

• Pekefingeren plasseres etter vektoren til
• Med langfingeren følger vektoren b
• Tommelen, utvidet, indikerer retningen og retningen på vektoren R.

Denne ordren må følges nøyaktig, siden vektorproduktet ikke er kommutativt, det vil si til × b ≠ b × til Og hvis vektorene blir utvekslet, vil det ikke oppnås riktig resultat.

Kan tjene deg: eksistens og unikhet teorem: demonstrasjon, eksempler og øvelser

Leseren anbefales å plassere høyre hånd som figuren viser, indeksen som peker mot venstre representerer vektoren til, Langfingeren følger b Og den peker direkte på leseren, til slutt, tommelen indikerer opp, og peker på retningen og retningen på vektoren til × b = R.

Cruz produktegenskaper

-Kors- eller vektorproduktet mellom to vektorer resulterer alltid i en annen vektor.

-Et kryssprodukt er ikke kommutativt, derfor: til × b ≠ b × til.

-For kryssproduktet er det sant at: til × b = - (b × til). Denne egenskapen kalles anti-konminitet.

-Den resulterende vektoren til vektorproduktet mellom to vektorer er vinkelrett (normal) til nevnte vektorer.

-Fra ovenstående følger det at vektorproduktet mellom vektorer med samme retning er null. Spesielt til × A = 0.

-Kryssproduktet er i samsvar med distribusjonsloven med hensyn til summen: til × (b+c) = til × b + til × c

-Hvis m er en skalar, så m (til × b) = m til × b = til × m b

Kryss produkt mellom enhetsvektorer

De tre enhetsvektorene, kalt Yo, J og k, De er vinkelrett på hverandre og indikerer de tre bemerkelsesverdige romens retninger: høy, bred og dybde. Disse adressene er vinkelrett på hverandre.

Vektorproduktet mellom enhetsvektorene bestemmes enkelt gjennom høyre regel og husk egenskapene til kryssproduktet:

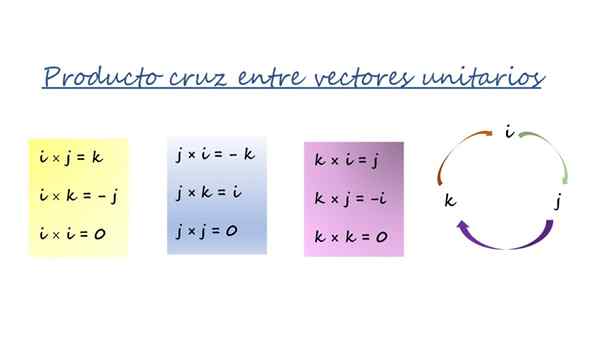Vektorprodukt av kartesiske enhetsvektorer. Kilde: f. Zapata.

De tre fargede boksene i figuren er oppsummert i runden med piler til høyre og brukes på denne måten:

-Når du multipliserer i pilens retning, er resultatet vektoren foran pilen og har et positivt tegn. For eksempel ved å multiplisere vektorly J og k, Den tredje vektoren er Yo, Og etter hvert som ordren følger betydningen av pilen, er tegnet +.

Kan tjene deg: vektorfunksjoner

-Og hvis det multipliserer i motsatt retning av pilen, er resultatet den tredje vektoren foran pilen, men med et negativt tegn.

Enhetsvektorene utgjør en base, slik at enhver annen vektor kan skrives i form av dem. Dette letter beregningen av kryssproduktet mellom to vilkårlige vektorer i verdensrommet i stor grad.

Hvordan man analyserer kryssproduktet til to vektorer analytisk

Når vektorer til og b De har en vilkårlig retning i verdensrommet, med komponenter langs hver av dem, det er lettere å beregne kryssproduktet på en analytisk måte, og uttrykker dem med tanke på enhetsvektorene Yo, J og k:

• til = a_x Yo + til_og J + til_z k
• b = b_x Yo + b_og J + b_z k

Nå brukes distribusjonsegenskapen til multiplikasjon, som også er gyldig for kryssproduktet:

til × b = (a_x Yo + til_og J + til_z k) × (B_x Yo + b_og J + b_z k) =

= (a_x Yo × b_x Yo) + (a_x Yo × b_og J) + (a_x Yo × b_z k) + (a_OG J × b_x Yo) + (a_OG J × b_og J) + (a_OG J × b_z k) + (a_Z k × b_x Yo) + (a_Z k × b_og J) + (a_Z k × b_z k)

Kryssprodukter mellom like enhetsvektorer blir kansellert, ettersom de er parallelle vektorer, noe som reduserer dette uttrykket til 6 termer:

til × b = (a_x Yo × b_og J) + (a_x Yo × b_z k) + (a_OG J × b_x Yo) + (a_OG J × b_z k) + (a_Z k × b_x Yo) + (a_Z k × b_og J)

Til slutt, ved å bruke figuren over, resulterer hvert produkt i:

til × b = a_x b_og k + til_x b_z ( -J) + a_OG b_x ( -k) + a_OG b_z Yo + til_Z b_xJ + til_Z b_og ( -Yo) =

= (a_OG b_z - a_Z b_og) Yo + (til_Z b_x - a_x b_z) J + (til_x b_og - a_OG b_x) k

Cruz -produkt gjennom en determinant

Det er ikke nødvendig å huske formelen ovenfor, men bruker enkelt runde for den foregående figuren eller ganske enkelt utfør det determinanten som er vist nedenfor, noe som er helt likeverdig:

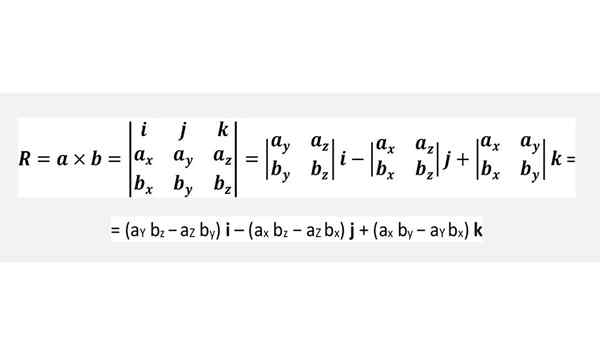
Eksempel

Forutsatt vektorer til og b er:

• til = 5 Yo - J + 4 k
• b = -Yo + 0J +7 k

Kryssproduktet mellom dem beregnes ved å identifisere og erstatte de respektive koordinatene:

Kan tjene deg: Hyperbolsk paraboloid: Definisjon, egenskaper og eksempler

til_x = 5; til_og = −1; til_z = 4; b_x = −1; b_og = 0: b_z = 7

til × b = [(−1) ∙ 7 - 4 ∙ 0] Yo + [(4 ∙ (−1) - 5 ∙ 7) J + [5 ∙ 0 - (−1) ∙ (−1)] k = [−7 - 0] Yo + [(−4 - 35) J + [0 - 1] k =

= (−7) Yo - 39 J - k

Den determinantmetoden gir samme resultat.

Trening

Beregn med determinanter, kryssproduktet mellom vektorene:

• eller = 2 Yo +J + 5 k
• v = Yo + 4J +7 k

Og bestemme området til parallellogrammet underlagt av de tidligere vektorene, som vist på figuren:

Løsning

Verdier av vektorkoordinater erstattes i determinanten:

Det bestemte parallellogramområdet er modulen til vektorproduktet mellom dem, noe som resulterer: r = 17,3 arealenheter.