Bemerkelsesverdige produkter

Hva er bemerkelsesverdige produkter?

Bemerkelsesverdige produkter er algebraiske operasjoner, der multiplikasjoner av polynomer er uttrykt, som ikke trenger å bli løst tradisjonelt, men ved hjelp av visse regler kan resultatene av det samme bli funnet.

Polynomer multipliseres med om det derfor er mulig at de har mange termer og variabler. For å gjøre prosessen kort, brukes reglene for de bemerkelsesverdige produktene, som tillater multiplikasjoner uten å måtte gå termin for termin.

Bemerkelsesverdige produkter og eksempler

Hvert bemerkelsesverdig produkt er en formel som følger av en faktorisering, sammensatt av polynomer av flere begreper som binomials eller trinomials, kalt faktorer.

Faktorene er grunnlaget for en makt og har en eksponent. Når faktorene formidler, må eksponentene legges til.

Det er flere bemerkelsesverdige produktformler, noen er mer brukt enn andre, avhengig av polynomer, og er følgende:

Firkantet binomial

Det er multiplikasjonen av en binomial av seg selv, uttrykt i form av makt, der begrepene legges til eller trukket fra:

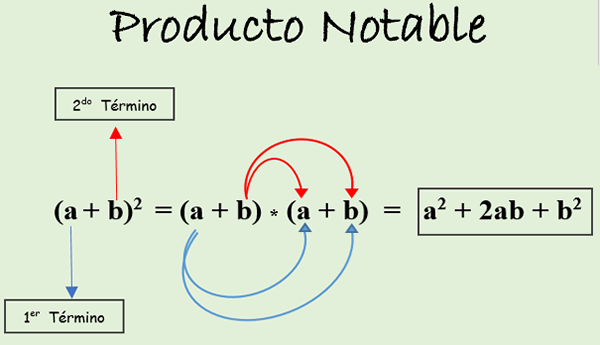
til. Firkantet sum binomial: Det er lik kvadratet på første periode, pluss dobbelt produktet av vilkårene, pluss kvadratet på den andre termen. Det uttrykkes som følger:

(A + B)² = (a + b) _* (A + B).

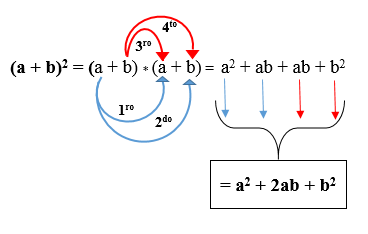
I den følgende figuren kan du se hvordan produktet er utviklet i henhold til den nevnte regelen. Resultatet kalles trinomial av et perfekt firkant.

Eksempel 1

(x + 5) ² = x² + 2 (x * 5) + 5²

(x + 5) ² = x² + 2 (5x) + 25

(x + 5) ² = x² + 10x + 25.

Eksempel 2

(4a + 2b) = (4a)² + 2 (fjerde _* 2b) + (2b)²

(4a + 2b) = 8a² + 2 (8ab) + 4b²

(4a + 2b) = 8a² + 16 AB + 4B².

b. Binomial av en firkantet subtraksjon: Den samme regelen om binomialen til en sum blir brukt, bare at i dette tilfellet er den andre perioden negativ. Formelen er som følger:

(A - B)² = [(a) + (- b)]²

Kan tjene deg: Numeriske analogier: Typer, applikasjoner og øvelser

(A - B)² = a² +2 _* (-b) + (-b)²

(A - B)²   = a² - 2ab + b².

Eksempel 1

(2x - 6)² = (2x)² - 2 (2x _* 6) + 6²

(2x - 6)²  = 4x² - 2 (12x) + 36

(2x - 6)² = 4x² - 24x + 36.

Konjugate Binomials Produkt

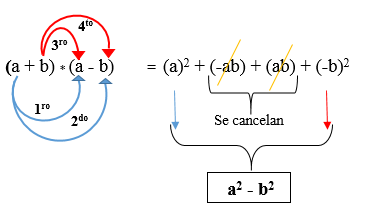
To binomials er konjugert når de andre begrepene for hvert er av forskjellige tegn, det vil si at det for det første er positivt og at av det andre negative eller omvendt. Det løses ved å heve hver monomial kvadrat og trukket fra. Formelen er som følger:

(A + B) _* (A - B)

I den følgende figuren er produktet av to konjugerte binomialer utviklet, der det observeres at resultatet er en forskjell på firkanter.

Eksempel 1

(2a + 3b) (2a - 3b) = 4a² + (-6ab) + (6 ab) + (-9b²)

(2a + 3b) (2a - 3b) = 4a² - 9b².

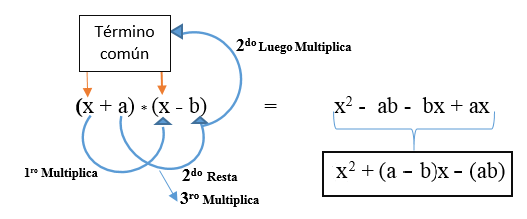
Produkt av to binomialer med et felles begrep

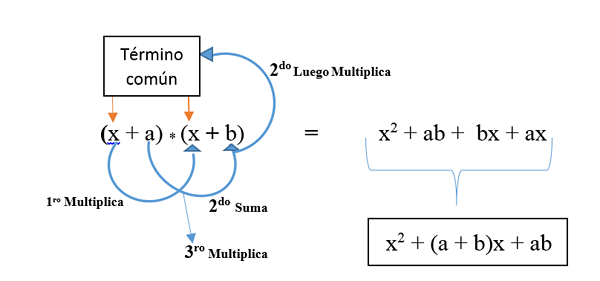
Det er et av de mest komplekse og lite brukte bemerkelsesverdige produktene fordi det er en multiplikasjon av to binomialer som har et felles begrep. Regelen indikerer følgende:

• Kvadratet med det vanlige begrepet.
• Pluss summen av vilkårene som ikke er vanlige, og multipliser dem deretter med det vanlige begrepet.
• Pluss summen av multiplikasjonen av vilkårene som ikke er vanlige.

Det er representert i formelen: (x + a) _* (x + b) og er utviklet som vist på bildet. Resultatet er en ikke -perfekt firkantet trinomial.

Eksempel 1

(x + 6) _* (x + 9) = x² + (6 + 9) _* X + (6 _* 9)

(x + 6) _* (x + 9) = x² + 15x + 54.

Det er muligheten for at den andre begrepet (det forskjellige begrepet) er negativ og formelen er som følger: (x + a) _* (x - b).

Eksempel 2

(7x + 4) _* (7x - 2) = (7x _* 7x) + (4 - 2)_* 7x + (4 _* -2)

(7x + 4) _* (7x - 2) = 49x² + (2)_* 7x - 8

(7x + 4) _* (7x - 2) = 49x² + 14x - 8.

Det kan også være tilfelle at begge forskjellige begrepene er negative. Formelen din vil være: (x - a) _* (x - b).

Kan tjene deg: Lamy teorem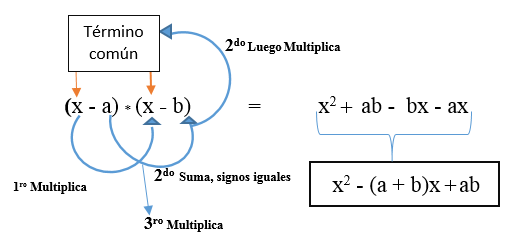

Eksempel 3

(3B - 6) _* (3B - 5) = (3B _* 3b) + (-6 - 5)_* (3b) + (-6 _* -5)

(3B - 6) _* (3b - 5) = 9b² + (-elleve) _* (3b) + (30)

(3B - 6) _* (3b - 5) = 9b² - 33b + 30.

Firkantet polynom

I dette tilfellet er det mer enn to begreper, og for å utvikle det, blir hver enkelt kuttet og tilsetter sammen med dobbelt multiplikasjon av ett begrep med et annet; Formelen er: (a + b + c)² Og resultatet av operasjonen er en trinomial kvadrat.

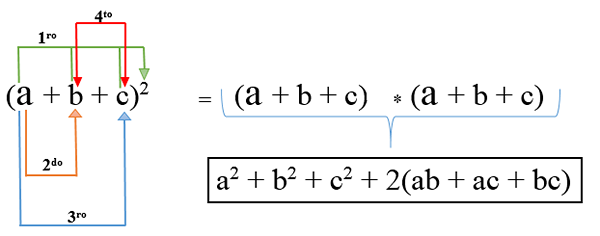
Eksempel 1

(3x + 2y + 4z)² = (3x)² + (2 og)² + (4Z)² + 2 (6xy + 12xz + 8yz)

(3x + 2y + 4z)² = 9x² + 4y² + 16Z² + 12xy + 24xz + 16yz.

Cube Binomial

Det er et komplekst bemerkelsesverdig produkt. For å utvikle det, multipliseres binomialen med firkanten, som følger:

til. For binomial til kuben til en sum:

• Den første termkuben, pluss tredoblet torget i første periode etter den andre.
• Pluss trippel den første perioden, av den andre kvadratet.
• Pluss kuben til den andre perioden.

(A + B)³ = (a + b) _* (A + B)²

(A + B)³ = (a + b) _* (til² + 2ab + b²)

(A + B)³ = a³ + 2²B + AB² + ba² + 2ab² + b³

(A + B)³ = a³ + 3²B + 3AB² + b³.

Eksempel 1

(A + 3)³ = a³ + 3 (a)²_*(3) + 3 (a)_*(3)² + (3)³

(A + 3)³ = a³ + 3 (a)²_*(3) + 3 (a)_*(9) + 27

(A + 3)³ = a³ + 9 a² + 27a + 27.

b. For binomialen til kuben til en subtraksjon:

• Kuben til første periode, bortsett fra trippel av torget i første periode av den andre.
• Pluss trippel den første perioden, av den andre kvadratet.
• Mindre kuben til den andre terminen.

(A - B)³ = (a - b) _* (A - B)²

(A - B)³ = (a - b) _* (til² - 2ab + b²)

(A - B)³ = a³ - 2²B + AB² - ba² + 2ab² - b³

(A - B)³ = til³ - 3²B + 3AB² - b³.

Eksempel 2

(B - 5)³ = b³ + 3 (b)²_*(-5) + 3 (b)_*(-5)² + (-5)³

(B - 5)³ = b³ + 3 (b)²_*(-5) + 3 (b)_*(25) -125

Kan tjene deg: Ikke -grupperte data: Eksempler og trening løst

(B - 5)³ = b³ - 15b² +75B - 125.

Trinomial kube

Den utvikler seg med å multiplisere den med torget. Det er et veldig omfattende bemerkelsesverdig produkt fordi det er 3 begreper hevet til kuben, pluss trippel for hvert firkantet begrep, multiplisert med hvert av vilkårene, pluss seks ganger produktet av de tre begrepene. Sett i en bedre form:

(A + B + C)³ = (A + b + c) _* (A + B + C)²

(A + B + C)³ = (A + b + c) _* (til² + b² + c² + 2AB + 2AC + 2BC)

(A + B + C)³ = A³ + b³ + c³ + 3²B + 3AB² + 3²C + 3AC² + 3b²C + 3BC² + 6ABC.

Eksempel 1

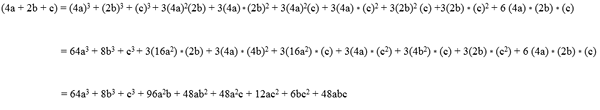
Løste øvelser med bemerkelsesverdige produkter

Oppgave 1

Utvikle følgende binomial til kuben: (4x - 6)³.

Løsning

Husker at en binomial til kuben er lik den første termen som er hevet til kuben, bortsett fra trippel av torget til den første termin av den andre; pluss tredoblet den første termin, av den andre kvadratet, bortsett fra kuben til den andre terminperioden.

(4x - 6)³ = (4x)³ - 3 (4x)²(6) + 3 (4x) _* (6)² - (6)²

(4x - 6)³ = 64x³ - 3 (16x²) (6) + 3 (4x)_* (36) - 36

(4x - 6)³ = 64x³ - 288x² + 432x - 36.

Oppgave 2

Utvikle følgende binomial: (x + 3) (x + 8).

Løsning

Du har en binomial der det er et felles begrep, som er x og den andre termen er positiv. For å utvikle det, må bare det vanlige uttrykket økes, pluss summen av vilkårene som ikke er vanlige (3 og 8) og deretter multiplisere dem med det vanlige begrepet, pluss summen av multiplikasjonen av begrepene som ikke er vanlige.

(x + 3) (x + 8) = x² + (3 + 8) x + (3_*8)

(x + 3) (x + 8) = x² + 11x + 24.

Referanser

1. Angel, a. R. (2007). Elementær algebra. Pearson Education,.
2. Arthur Goodman, L. H. ( nitten nittiseks). Algebra og trigonometri med analytisk geometri. Pearson Education.
3. Das, s. (s.F.). Matematikk pluss 8. Storbritannia: Sagar Ratna.
4. Jerome e. Kaufmann, k. L. (2011). Elementær og mellomliggende algebra: En kombinert tilnærming. Florida: Cengage Learning.
5. Pérez, ca. D. (2010). Pearson Education.