Sum assosiativ eiendom, multiplikasjon, eksempler, øvelser

De Assosiativ eiendom av summen representerer den assosiative naturen til operasjonen legger til i forskjellige matematiske sett. Det knytter tre (eller flere) elementer i disse settene, kalt A, B og C, slik at det alltid er oppfylt:

a + (b + c) = (a + b) + c

På denne måten er det garantert at uansett hvordan man grupperer for å utføre operasjonen, er resultatet det samme.

Figur 1. Vi bruker den tilknyttede egenskapen til summen mange ganger når vi utfører aritmetikk og algebraisk operasjoner. (Tegning: Freepik Sammensetning: F. Zapata)

Men det skal bemerkes at assosiativ egenskap ikke er synonymt med kommutativ eiendom. Det vil si at vi vet at rekkefølgen på tilleggene ikke endrer summen eller at rekkefølgen på faktorene ikke endrer produktet. Så for summen kan du skrive slik: a + b = b + a.

Imidlertid er det i den assosiative egenskapen annerledes, siden rekkefølgen på elementene som skal legges til, opprettholdes og hvilke endringer er operasjonen som utføres først. Noe som betyr at det ikke spiller noen rolle først (B+C) og til dette resultatet legg til, for å begynne å legge til B og til resultatet legg til C.

Mange viktige operasjoner som summen er assosiative, men ikke alle. For eksempel i subtraksjon av reelle tall skjer det at:

A - (B - C) ≠ (A - B) - C

Ja A = 2, B = 3, C = 1, da:

2- (3 - 1) ≠ (2 - 3) - 1

0 ≠ -2

[TOC]

Assosiativ egenskap av multiplikasjon

Som det ble gjort for summen, indikerer multiplikasjonens assosiative eiendom at:

a ˟ (b ˟ c) = (a ˟ b) ˟ c

Kan tjene deg: sum av polynomer, som gjøres, eksempler, øvelser

Når det gjelder settet med reelle tall er det enkelt å bekrefte at det alltid er. For eksempel ved å bruke verdier a = 2, b = 3, c = 1, må du for eksempel:

2 _˟ (3 _˟ 1) = (2 _˟  3) _˟ 1 → 2 _˟ 3 = 6 _˟ 1

6 = 6

De reelle tallene oppfyller den tilknyttede egenskapen til både sum og multiplikasjon. På den annen side, i et annet sett, som vektorene, er summen assosiativ, men kryssproduktet eller vektorproduktet er ikke.

Bruksområder for den assosiative egenskapen til multiplikasjon

En fordel som operasjonene der den assosiative eiendommen er oppfylt, skal gruppere på den mest praktiske måten blir oppfylt. Dette letter oppløsningen sterkt.

Anta for eksempel at det i et lite bibliotek er 3 hyller med 5 underholdning hver. I hver underholdning er det 8 bøker. Hvor mange bøker er totalt?

Vi kan utføre operasjonen som følger: Total bøker = (3 x 5) x 8 = 15 x 8 = 120 bøker.

Eller så: 3 x (5 x 8) = 3 x 40 = 120 bøker.

Figur 2. En anvendelse av den assosiative egenskapen til multiplikasjon er å beregne antall bøker på hver hylle. Bilde laget av f. Zapata.

Eksempler

-I settene med naturlige, hele, rasjonelle, reelle og komplekse tall er den assosiative egenskapen til summen og multiplikasjonen oppfylt.

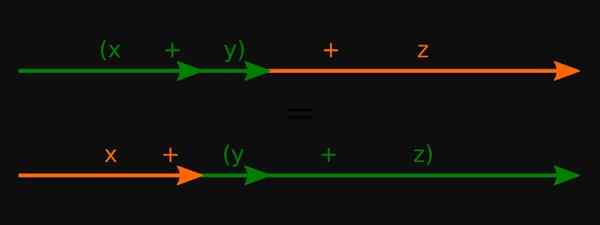Figur 3. For reelle tall er summen til den tilknyttede egenskapen oppfylt. Kilde: Wikimedia Commons.

-For polynomer bruker de også i disse operasjonene.

-I tilfeller av subtraksjonsoperasjoner, inndeling og eksponentiering, blir ikke assosiativ eiendom oppfylt i reelle antall eller polynomer.

Kan tjene deg: orthoedro: Formler, område, volum, diagonal, eksempler

-Når det. Dette betyr at gitt matriser A, B og C, er det sant at:

(A x b) x c = a x (b x c)

Men ... a x b ≠ b x a

Assosiativ egenskap i vektorer

Vektorer danner et annet sett enn reelle tall eller komplekse tall. Operasjonene som er definert for settet med vektorer er noe forskjellige: det er sum, subtraksjon og tre typer produkter.

Summen av vektorer oppfyller den assosiative egenskapen, så vel som antall, polynomer og matriser. Når det gjelder skalarproduktene, klatring av vektor og kryss som er laget mellom vektorer, oppfyller sistnevnte ikke, men skalarproduktet, som er en annen type operasjon mellom vektorer, oppfyller det, med hensyn til følgende:

-Produktet av en skalar for en vektor resulterer i en vektor.

-Og ved å klatre på to vektorer er det en skalar.

Derfor gitt vektorene v, eller og W, Og i tillegg en skalar λ, er det mulig å skrive:

-Sum av vektorer: v +(eller + W ) = (v + eller) + W

-Skalarprodukt: λ (v • eller ) = (λv) • eller

Sistnevnte er mulig takket være hva v • eller Det er en skalar, og λv Det er en vektor.

Derimot:

v × (eller × W ) ≠ (v × eller)×W

Polynomfaktorisering ved å gruppere termer

Denne applikasjonen er veldig interessant, for som nevnt ovenfor, hjelper Associative eiendommer å løse visse problemer. Summen av monomialer er assosiativ, og dette kan brukes til å faktorere når en åpenbar felles faktor ikke vises ved første blikk.

Kan tjene deg: konveks polygon: definisjon, elementer, egenskaper, eksempler

Anta for eksempel at det blir bedt om å faktorere: x³ + 2x² + 3x +6. Dette polynomet mangler en felles faktor, men la oss se hva som skjer hvis det er gruppert på denne måten:

x³ + 2x² + 3x +6 = (x³ + 2x²) + (3x +6)

Den første parentesen har som en vanlig faktor x²:

x³ + 2x² = x² (x+2)

I den andre er den vanlige faktoren 3:

3x +6 = 3 (x + 2)

Så:

x³ + 2x² + 3x +6 = x²(x+ 2)+ 3 (x+ 2)

Nå er det en åpenbar felles faktor, som er x+2:

x²(x+ 2)+ 3 (x+ 2) = (x+ 2) (x²+3)

Øvelser

- Oppgave 1

Bygningen av en skole har 4 etasjer, og i hver er det 12 klasserom med 30 pulter inne. Hvor mange pulter har skolen totalt?

Løsning

Dette problemet løses ved å anvende den assosiative egenskapen til multiplikasjon, la oss se:

Totalt antall pulter = 4 etasjer x 12 Klasserom /gulv x 30 pulter /klasserom = (4 x 12) x 30 pulter = 48 x 30 = 1440 pulter.

O Hvis foretrukket: 4 x (12 x 30) = 4 x 360 = 1440 pulter

- Oppgave 2

Gitt polynomene:

A (x) = 5x³ + 2x² -7x + 1

B (x) = x⁴ +6x³ -5x

C (x) = -8x² +3x -7

Bruk den tilknyttede egenskapen til summen for å finne (x) + b (x) + c (x).

Løsning

De to første kan grupperes og resultatet legger til det tredje:

A (x) + b (x) = [5x³ + 2x² -7x + 1] + [x⁴ +6x³ -5x] = x⁴ + 11x³+ 2x² -12x +1

Polynom C (x) legges umiddelbart til:

[x⁴ + 11x³+ 2x² -12x +1] + [-8x² +3x -7] = x⁴ + 11x³ - 6x² -9x -6

Leseren kan bekrefte at resultatet er identisk hvis det løses etter alternativ a (x) + [b (x) + c (x)]].

Referanser

1. Jiménez, r. 2008. Algebra. Prentice Hall.
2. Matematikk er morsomt. Kommutative, assosiative og distriktslover. Gjenopprettet fra: Mathisfun.com.
3. Matematikk lager. Definisjon av assosiativ eiendom. Gjenopprettet fra: Mathwarehouse.com.
4. Scienting. Assosiativ og kommutativ egenskap av tillegg og multiplikasjon (med eksempel). Gjenopprettet fra: Scienting.com.
5. Wikipedia. Assosiativ eiendom. Hentet fra: i.Wikipedia.org.