Hjemmeside
Matte
Begrens egenskaper (med eksempler)

Matte

Begrens egenskaper (med eksempler)

De Begrense egenskapene De er settet med algebraiske regler og prosedyrer som brukes for å bestemme dem. Grensekonseptet er viktig for beregning, og å finne verdien trenger ikke å være en komplisert oppgave, forutsatt at egenskapene håndteres med letthet.

Nedenfor er en liste over det viktigste, ledsaget av applikasjonseksempler.

Grensene og dens egenskaper er grunnlaget for beregning. En veldig spesiell grense er vist på figuren: Derivatet av en F (x) funksjon

La B, C, N, A og B reelle tall, og F og g Slike funksjoner som verifiserer følgende:

$\lim_x\rightarrow cf(x)=A$
$\lim_x\rightarrow cg(x)=B$

Da har du følgende egenskaper:

1. Direkte erstatningsgrense

I første omgang kan grensen for en funksjon f når x → c kan beregnes direkte å erstatte x = c i funksjonen. Hvis funksjonen eksisterer ved x = c, er grensen:

$\lim_x \rightarrow c f(x)=f(c)$ Men ikke nødvendigvis må funksjonen defineres ved x = c slik at grensen eksisterer. Tanken er å nærme deg så mye du vil verdien av x = c og se hva som skjer med funksjonen i så fall.

Eksempel

Finn grensen på f (x) = x² Når x → 4

Løsning

Grensen løser seg ganske enkelt ved å erstatte x = 4 i f (x) = x², Siden det ikke er noen ulempe med å utføre operasjonen:

$\lim_x\rightarrow 4x^2=4^2=16$ 2. Unikhet med grensen

Hvis grensen for en funksjon f (x) når x → c eksisterer og er verdt l, er det unik, er unik.

Derfor sidegrensene, som er de når x → c^- (Les “X har en tendens til C fra venstre”) Og når x → C⁺(Den lyder “X har en tendens til C til høyre”), eksisterer begge og har samme verdi L, selv om funksjonen ikke er definert i x = C.

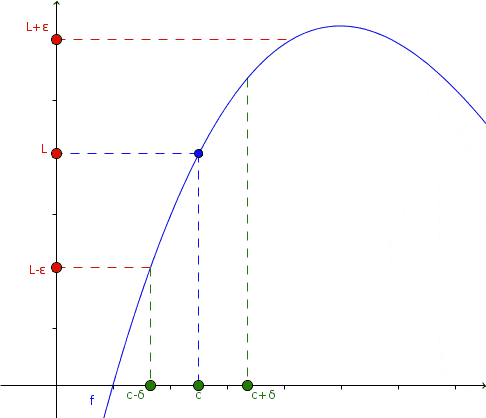I denne animasjonen presenteres begrensningsbegrepet: Når x har en tendens til en viss verdi C, og nærmer seg både til venstre og høyre, har verdien av funksjonen en tendens til l. Ikke nødvendigvis er funksjonen definert i x = c. Kilde: Wikimedia Commons.

I animasjonen blir denne tilnærmingen observert og hva som skjer med funksjonen i så fall: Enten den nærmer seg til venstre og til høyre til X = C, er verdien av funksjonen på sin side nær L.

Kan tjene deg: minimums torg

Matematisk uttrykker på denne måten:

$\lim_x\rightarrow c^-f(x)=\lim_x\rightarrow c^+f(x)=\lim_x\rightarrow cf(x)=L$ Sidegrensene gjør det mulig å vite når en grense eksisterer eller ikke, for hvis de ikke eksisterer, eller hvis de er forskjellige, er det sikkert at grensen for funksjonen når x → C ikke eksisterer.

Eksempel

Beregn grensen for f (x) når x → 1 hvis den eksisterer, hvor f (x) er gitt av:

Løsning

Dette er en funksjon av deler eller definert i stykker, som består av linje 4 -x for verdiene til x < 1 y en la parábola 4 - x² Når x er lik 1 eller større enn 1.

Vi kan nærme oss x = 1 fra venstre, i dette tilfellet er den delen av funksjonen som er gyldig for x tatt<1:

Ettersom sidegrensene er de samme, følger det at grensen for funksjonen når x → 1 eksisterer og er verdt 3.

3. Konstant

Grensen for en konstant er verdien av nevnte konstant, uavhengig av verdien som variabelen har en tendens til:

$\lim_x\rightarrow cb=b .$

Eksempel

Regne ut:

$\lim_x\rightarrow 1\pi$ Løsning

$\lim_x\rightarrow 1\pi= \pi$

4. Identitetsfunksjonsgrense

Hvis f (x) = x, blir det alltid oppfylt det:

$\lim_x\rightarrow cx=c$

Eksempel

Regne ut:

$\lim_x\rightarrow 2x$ Løsning

$\lim_x\rightarrow 2x=2$

5. Produktgrense for en konstant med en funksjon

I dette tilfellet går konstanten ut av grensen og beveger seg for å multiplisere den, slik:

$\lim_x\rightarrow c\left [b\cdot f(x) \right ]=b\cdot \lim_x\rightarrow c f(x)=b\cdot A$ Eksempel

Beregn, hvis det eksisterer, følgende grense:

$\lim_x\rightarrow -2\left [5\cdot x^3 \right ]$ Løsning

Konstanten 5 er utenfor multipliserer til grensen og erstatningsegenskapen brukes:

$\lim_x\rightarrow -2\left [5\cdot x^3 \right ]=5\cdot \lim_x\rightarrow -2 x^3=5\cdot (-2)^3=-40$

6. Sumgrense

Grensen for summen av to funksjoner F og g Det er summen av grensene:

$\lim_x\rightarrow c\left [ f(x)+g(x) \right ]=\lim_x\rightarrow c f(x)+\lim_x\rightarrow cg(x)=A+B$

Eksempel

Finn følgende grense hvis den eksisterer:

Kan tjene deg: sett teori: egenskaper, elementer, eksempler, øvelser

$\lim_\theta \rightarrow \pi \left [cos\:\theta +sen\: \theta \right ]$ Løsning

Eiendommen til summen av grensene brukes først og deretter den for direkte erstatning, siden operasjonene ikke har vanskeligheter:

$\lim_\theta \rightarrow \pi \left [cos\:\theta +sen\: \theta \right ] = \lim_\theta \rightarrow \pi cos\: \: \theta + \lim_\theta \rightarrow \pisen\: \: \theta=cos\: \pi +sen\: \pi =-1$

7. Subtraksjonsgrense

Ved grensen for subtraksjon av to funksjoner, fortsett på en analog måte som for summen: grensen for subtraksjon er subtraksjon av grensene:

$\lim_x\rightarrow c \left [f(x) - g(x) \right ]=A-B$

Eksempel

Beregn følgende grense:

$\lim_x \rightarrow 0 [sec\: x - e^x ]$ Løsning

Egenskapen til subtraksjonsgrensen for to funksjoner blir brukt og deretter direkte erstatning, siden alle operasjoner kan utføres uten problem:

$\lim_x \rightarrow 0 [sec\: x - e^x ]=\lim_x \rightarrow 0 sec\: x -\lim_x \rightarrow 0 e^x = sec\: 0-e^0=1-1=0$

8. Produktgrense

Produktgrensen for to funksjoner F og g Det er produktet av grensene:

$\lim_x \rightarrow c [f(x)\cdot g(x) ]=\lim_x \rightarrow c f(x) \cdot \lim_x \rightarrow c g(x) = A\cdot B$ Eksempel

Beregn denne grensen:

$\lim_x \rightarrow 0 cos\: x\cdot (1-x^2^)$

Løsning

$\lim_x \rightarrow 0 cos\: x\cdot (1-x^2^)=\lim_x \rightarrow 0 cos\: x\cdot \lim_x \rightarrow 0 (1-x^2^)=cos\: 0\cdot (1-0^2)=1$

9. Forholdet mellom kvotienten

Grensen for forholdet mellom to funksjoner F og g Det er grensen. Så:

$\lim_x \rightarrow c \left [ \fracf(x)g(x) \right ]=\frac\lim_x \rightarrow c f(x)\lim_x \rightarrow c g(x)=\fracAB; \: \: \textupcon\: B\neq 0$

Eksempel

Beregn, hvis det eksisterer, verdien av følgende grense:

$\lim_x \rightarrow -3 \left [ \frac2x-6x^2+5 \right ]$ Løsning

I første omgang brukes eiendomsgrensen egenskapen, for å oppnå grensenes kvotient:

$\lim_x \rightarrow -3 \left [ \frac2x-6x^2+5 \right ]=\frac\lim_x \rightarrow -3 2x-6\lim_x \rightarrow -3 x^2+5$

Erstatningsegenskapen brukes nå for å finne hver grense:

$\lim_x \rightarrow -3 2x-6=2\cdot (-3)-6=-12$ $\lim_x \rightarrow -3 x^2+5= (-3)^2+5=14$

Og siden B ≠ 0, er grensen som er søkt kvotten A/B:

$\lim_x \rightarrow -3 \frac2x-6x^2+5=\frac-1214=\frac-67$

10. Grense

Grensen for en eksponentkraft N tilsvarer grensen som er hevet til nevnte makt, som følger:

$\lim_x \rightarrow c \left [f(x) \right ]^n=\left [\lim_x \rightarrow c f(x) \right ]^^n$ Sak 1: Grense for en X -kraft

Hvis du for eksempel har grensen for en X -kraft, resultater:

$\lim_x \rightarrow c x^n=\left [\lim_x \rightarrow c x \right ]^n$

I følge eiendom 4 er denne grensen:

Kan tjene deg: Numeriske analogier: Typer, applikasjoner og øvelser

$\lim_x \rightarrow c x^n=c^n$

Sak 2: Rotgrense

En n-denne roten kan skrives i form av en brøkeksponent, derav:

$\lim_x \rightarrow c \sqrt[n]f(x)=\sqrt[n]\lim_x \rightarrow c f(x)$

Viktig: Hvis rotindeksen er jevn, er det nødvendig at grensen for f (x) når x → c er større enn eller lik 0, siden det ikke er noen reelle par negative mengder.

Eksempler

Bestem, bruk de tidligere egenskapene, følgende grenser hvis de eksisterer:

$a)\: \lim_x \rightarrow -2 (x+5)^^3$

$b)\: \lim_x \rightarrow 3 \sqrt2x-1$

Løsning på

Ved eiendom av grensen for en makt og direkte substitusjon oppnås det:

$\lim_x \rightarrow -2 (x+5)^^3= \left [\lim_x \rightarrow -2 (x+5) \right ]^3=(-2+5)^3=27$

Løsning b

$\lim_x \rightarrow 3 \sqrt2x-1=\sqrt\lim_x \rightarrow 3 \left (2x-1 \right )=\sqrt(2\cdot 3-1)=\sqrt5$

elleve. Grense

For å finne grensen for en baseeksponentiell B og eksponent f (x), må basen til funksjonen til funksjonen f (x) heves som følger:

$\lim_x \rightarrow c \left [b^f(x) \right ]=b^\lim_x \rightarrow cf(x)$

Eksempel

Finn om det er følgende grense:

$\lim_x \rightarrow 1 \left [e^x^^2 \right ]$ Løsning

I denne grensen er basen tallet E og funksjonen f (x) = x², Derfor må du først beregne x -grensen² Når X har en tendens til 1:

$\lim_x \rightarrow 1 x^2=1^^2=1$

Deretter brukes egenskapen til eksponentiell grense:

$\lim_x \rightarrow 1 e^^x^2=e^^1=e$

12. Eksponentiell potensiell funksjonsgrense

Grensen når x → C for en funksjon f (x), som igjen er forhøyet til en annen funksjon G (x) uttrykkes av:

$\lim_x \rightarrow c \left [f(x)^g(x) \right ]=\left [\lim_x \rightarrow c f(x) \right ]^\lim_x \rightarrow c g(x)$

Eksempel

Beregn følgende grense, hvis den eksisterer:

$\lim_x \rightarrow -1 (x-1)^^2x$

Løsning

For å bruke den forrige egenskapen, identifiseres de først f (x) = x-1 og g (x) = 2x, og deretter beregnes de respektive grensene:

$\lim_x \rightarrow -1 (x-1)=-1-1=-2$

$\lim_x \rightarrow -1 2x=2\cdot (-1)=-2$ Endelig:

$\lim_x \rightarrow -1 (x-1)^2x=\left [\lim_x \rightarrow -1 (x-1) \right ]^\lim_x \rightarrow -1 2x=(-2)^-2=\left (\frac1-2 \right )^2=\frac14$ Referanser

Ayres, f. 2000. Beregning. 5ed. Mc Graw Hill.
Leithold, l. 1992. Beregning med analytisk geometri. Harla, s.TIL.
Gratis matematikkekster. Grenser. Gjenopprettet fra: Matematikk.Liibretexts.org.
Mathemovil. Lover og begrenser egenskaper. Gjenopprettet fra: Matemovil.com.
Larson, r. 2010. Beregning av en variabel. 9na. Utgave. McGraw Hill.
Purcell, e. J., Varberg, d., & Rigdon, s. OG. (2007). Beregning. Mexico: Pearson Education.
Universformler. Begrense egenskapene. Gjenopprettet fra: Universoformulas.com

Begrens egenskaper (med eksempler)

1. Direkte erstatningsgrense

Eksempel

Løsning

2. Unikhet med grensen

Eksempel

Løsning

3. Konstant

Eksempel

Løsning

4. Identitetsfunksjonsgrense

Eksempel

Løsning

5. Produktgrense for en konstant med en funksjon

Eksempel

Løsning

6. Sumgrense

Eksempel

Løsning

7. Subtraksjonsgrense

Eksempel

Løsning

8. Produktgrense

Eksempel

Løsning

9. Forholdet mellom kvotienten

Eksempel

Løsning

10. Grense

Sak 1: Grense for en X -kraft

Sak 2: Rotgrense

Eksempler

Løsning på

Løsning b

elleve. Grense

Eksempel

Løsning

12. Eksponentiell potensiell funksjonsgrense

Eksempel

Løsning

Referanser

Beste artikler

Hva er formativ lesing? Typer og betydning

Formativ lesing er en type lesing hvis mål er å lære om et spesifikt emne. Fremmer en modifisering i...

Hva er sekundære lymfoide organer?

Sekundære eller perifere lymfoide organer er organene som er ansvarlige for regulering av cellulære ...

$\lim_x\rightarrow 4x^2=4^2=16$ 2. Unikhet med grensen

$\lim_x\rightarrow 1\pi$ Løsning

$\lim_x\rightarrow 2x$ Løsning

$\lim_x\rightarrow c\left [b\cdot f(x) \right ]=b\cdot \lim_x\rightarrow c f(x)=b\cdot A$ Eksempel

$\lim_x\rightarrow -2\left [5\cdot x^3 \right ]$ Løsning

$\lim_\theta \rightarrow \pi \left [cos\:\theta +sen\: \theta \right ]$ Løsning

$\lim_x \rightarrow 0 [sec\: x - e^x ]$ Løsning

$\lim_x \rightarrow c [f(x)\cdot g(x) ]=\lim_x \rightarrow c f(x) \cdot \lim_x \rightarrow c g(x) = A\cdot B$ Eksempel

$\lim_x \rightarrow -3 \left [ \frac2x-6x^2+5 \right ]$ Løsning

$\lim_x \rightarrow c \left [f(x) \right ]^n=\left [\lim_x \rightarrow c f(x) \right ]^^n$ Sak 1: Grense for en X -kraft

$\lim_x \rightarrow 1 \left [e^x^^2 \right ]$ Løsning

$\lim_x \rightarrow -1 (x-1)^2x=\left [\lim_x \rightarrow -1 (x-1) \right ]^\lim_x \rightarrow -1 2x=(-2)^-2=\left (\frac1-2 \right )^2=\frac14$ Referanser