Hva er retningslinjen? (Geometri)

De direktiv I geometri består den av en kurve, overflate eller volum som forblir fast og bestemmer måten et geometrisk objekt dannes. For eksempel er andre kurver som koniske og revolusjonsflater, for eksempel den rette sirkulære sylinderen, for eksempel den rette sirkulære sylinderen.

Retningslinjekurven kan også være en omkrets. En rett sirkulær sylinder kan dannes ved å etterlate en radius ri -r rión ri.

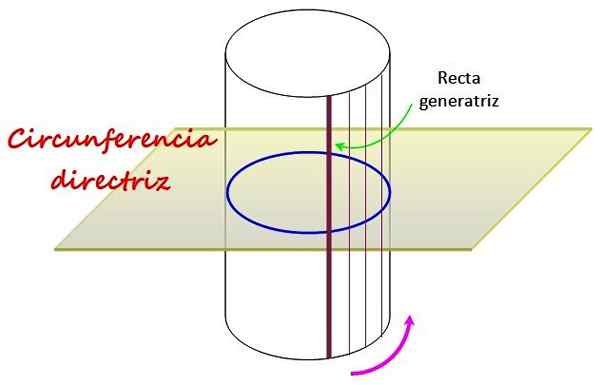
Figur 1. En rett sirkulær sylinder har som en guide en sirkel, som en rett linje kalt generatrix beveger seg. Kilde: f. Zapata.

Omkretsen, som er på planet tegnet i figuren, bestemmer formen på den buede overflaten til den rette sirkulære sylinderen, som genereres ved å rotere linjen rundt den, kalt Rett generatrix.

Hvis veiledningskurven ikke er en omkrets, men en annen kurve, genereres andre typer sylinder, for eksempel den elliptiske sylinderen, hvis retningslinje er en ellipse.

En omkrets kan også fungere som en retningslinje for å generere en annen kurve, slik er tilfellet med Epitrokoid, En kurve i flyet generert av et punkt, som igjen er i en mindre sirkel som ruller uten å gli, rundt retningslinjen.

Det er lettere å sette pris på det visuelt ved følgende animasjon:

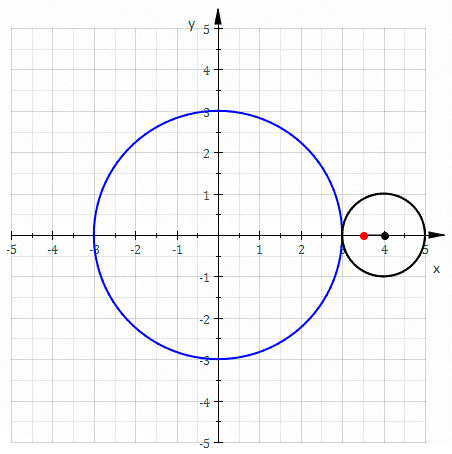Figur 2. Den røde kurven kalles Epitrocide og dens retningslinjekurve. Kilde: Wikimedia Commons. Sam Derbyshire på den engelske Wikipedia/CC BY-S (http: // CreativeCommons.Org/lisenser/by-SA/3.0/).

Retningslinjekurven på sylindriske overflater

Sylindriske overflater er klassifisert i henhold til deres retningslinjekurve i sylindere:

-Sirkulær

-Elliptisk

-Parabolsk

-Hyperbolsk

Når en sylindrisk overflate har en retningslinje som ligger i et plan vinkelrett på generatrix -linjen, er ligningen av nevnte overflate den samme som retningslinjen for retningslinjen.

Det kan tjene deg: Hva er forholdet mellom Rhombus -området og rektangelet?

Sylindrene tilhører gruppen av Kvadriske overflater, hvis ligning er andre klasse med tre variabler. Den generelle formen er:

Øks² + Av² + CZ² + Dxy + exz + fyz + gx + hy + iz + k = 0

Hvor koeffisienter A, B, C ... er reelle tall.

Sylindrene er de vanligste og nyttige tre -dimensjonale geometriske kroppene som finnes, spesielt de rette sirkulære sylindrene, men de andre typene sylindere beskrevet nedenfor har også applikasjoner innen ingeniørfag og design.

Rett sirkulær sylinder

Retningslinjen er en sirkel C som er i et plan vinkelrett på sylinderen, som vist i figur 1, siden generatrix -linjen, som går til C for å danne den laterale overflaten, er vinkelrett på C.

Ligningen av omkrets C på XY -planet, fokusert på opprinnelsen (0,0) er:

x² + og² = R²

Der R, vil omkretsens radius åpenbart være sylinderens radius. Høyden H på sylinderen strekker seg langs z -aksen, vinkelrett på XY -planet.

Elliptisk sylinder

Retningslinjen er en ellipse i XY -planet sentrert om opprinnelsen (0,0), hvis ligning er:

Generatrix er en linje vinkelrett på XY -planet, som beveger seg rundt ellipsen for å gi opphav til sideoverflaten. Ellipsen kan være i hvilken som helst høyde Z på XY -planet.

For eksempel ligningen ellipse:

4x² + 9y² = 36

Det er retningslinjekurven som gir opphav til den elliptiske sylinderen hvis ligning er 4x² + 9y² = 36, pluss z = 0. Legger til dette siste uttrykket, er det klart at det er overflaten.

Kan tjene deg: Prøvetakingsfeil: Formler og ligninger, beregning, eksempler

Parabolsk sylinder

I dette tilfellet er retningslinjen en lignelse, som kan være av skjemaet y = x². Dermed er sylinderen rettet langs z -aksen og danner stabling av lignelser med et toppunkt i (0,0) langs den aksen.

Den parabolske sylinderen har påføring i solenergi, siden noen samlere har speil på den måten, gjennom hvilke sollys er konsentrert i fokus. Dette punktet passerer et rett rør der en olje når temperaturer opp til 400 ºC.

Hyperbolsk sylinder

I den hyperbolske sylinderen er retningslinjens ligning hyperbola sentrert om opprinnelsen:

Sylinderen er dannet til stabelen.

Revolusjonsoverflate

Retningslinjekurven for en revolusjonsoverflate er den samme revolusjonsaksen, linjen som kurven som er ansvarlig for å generere overflaten.

Kurven som dreier seg kan ha vilkårlig form, på denne måten genereres et område som sett i denne animasjonen:

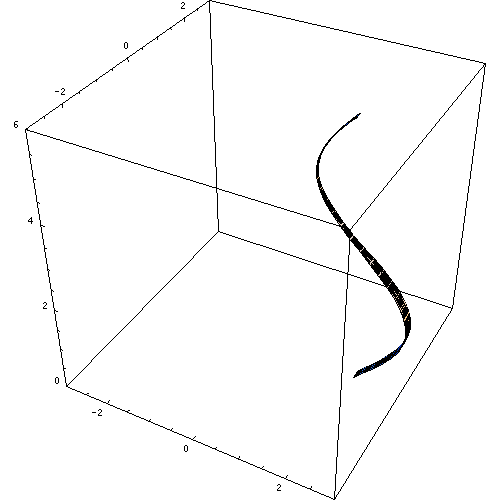Figur 3. En revolusjonsflate. Kilde: Wikimedia Commons. https: // last opp.Wikimedia.Org/wikipedia/commons/e/e7/rotationskoerper_animation.Gif.

Hvis en annen linje blir snudd rundt retningslinjen, oppnås den allerede kjente rette sirkulære sylinderen. På samme måte kan andre revolusjonsflater oppnås, for eksempel koniske, sfæriske og toroidale revolusjonsflater.

Konisk overflate

En konisk overflate genereres ved bevegelse av en generatrix -linje som alltid passerer gjennom den faste flate kurven eller retningslinjekurven og av det faste punktet som kalles Vertex, som ikke tilhører retningslinjens plan.

Kan tjene deg: Matematisk håp: Formel, egenskaper, eksempler, trening

Toppunktet eller spissen deler kjeglen i to deler, kalt Blader enten grener.

Løste øvelser

- Oppgave 1

Finn det laterale området til den høye sirkulære sylinderen med høyden 25 cm, hvis retningslinjekurve er 6 cm radiusomkrets, fokusert på opprinnelsen.

Løsning

Lateralområdet til sylinderen er produktet av lengden på retningslinjen etter høyde. Hvis R er omkretsens radius og H er høyden på sylinderen, er området gitt av:

A = 2πr x h = 2πx 6 cm x 25 cm = 942.5 cm²

- Oppgave 2

Du har følgende ligning som tilsvarer en kvadrisk overflate:

x² + og² + 2Z² +2xz - 2yz = 1

Angi hvilken overflate det er og hva som er likningen av retningslinjen.

Løsning

Gjør z = k, der k er konstant, oppnås det:

x² + og² + 2k² +2kx - 2Ky = 1

Vi omorganiserer vilkårene som følger:

(x² + 2kx) + (og²- 2Ky) = 1-2K²

Firkanter må², For ikke å endre noen av parentesene:

(x² + 2kx + k² - k² ) + (og² - 2Ky + k² - k²) = 1-2K²

(x² + 2kx + k²) - k²  + (og²- 2Ky + k²) - k² = 1-2k²

På denne måten gjenstår det:

(x + k)² + (og - k)² = 1

Som ligningen for en midtkrets (-K, K) og radius 1, er overflaten en rett sirkulær sylinder, også av radio 1, så lenge generatrix-linjen er vinkelrett på nevnte omkrets.

For eksempel, for eksempel k = 0, reduseres ligningen til omkretsen sentrert om opprinnelsen (0,0) hvis radius er 1:

x² + og² = 1

Referanser

1. Gaussere. Representere tre -dimensjonale overflater. Gjenopprettet fra: Gaussians.com.
2. Kindle, J. Teori og problemer med analytisk geometri. McGraw Hill. Schaum -serien.
3. Overflater som geometriske steder. Gjenopprettet fra: Algebra.Frlp.Utn.Edu.ar.
4. Suárez, m. Overflater. Hentet fra: fag.Unq.Edu.ar.
5. Kvadriske overflater. Gjenopprettet fra: systemer.fciencias.Unam.MX.