Hva som er kapasitiv reaktans og hvordan du beregner den?

De kapasitiv reaktans Det er motstanden at en kondensator, et regulatorisk element i belastningsstrømmen i en vekselstrømskrets, motsetter seg passering av strømmen.

I en krets som er sammensatt av en kondensator og aktivert av en vekselstrømkilde, kan kapasitiv reaktans x defineres_C følgende:

X_C = 1 / ωc

Figur 1. Kapasitive reaktanser er en del av Passabajos -filtre og høyttalere av høyttalere. Kilde: Pixabay.

Eller også:

X_C = 1 / 2πfc

Hvor C er kondensatorens kapasitet og ω er kildenes vinkelfrekvens, relatert til frekvensen F gjennom:

Ω = 2πf

Den kapasitive reaktansen avhenger av inverse av frekvensen, derfor ved høye frekvenser har en tendens til å være liten, mens ved lave frekvenser er reaktansen stor.

Den internasjonale systemenheten for å måle den kapasitive reaktansen er Ohm (ω), forutsatt at kondensatorens kapasitet er i Farad, (forkortet F) og frekvensen er uttrykt i det omvendte sekunder (s^-1).

Mens lasten varer, etableres også en spenning og en strøm gjennom kondensatoren, hvis maksimale amplituder eller verdier, betegnet som V som V_C og jeg_C, De er relatert gjennom kapasitiv reaktans analog med Ohms lov:

V_C = Jeg_C ⋅ x_C

I en kondensator blir spenningen forsinket 90º med hensyn til strømmen, eller den er avansert 90º med hensyn til den, som foretrukket. I alle fall er frekvensen den samme.

Når x_C Den er veldig stor, strømmen har en tendens til å være liten og gjøre verdien av x uendelig_C, Kondensatoren oppfører seg som en åpen krets og strømmen er null.

[TOC]

Hvordan beregne kapasitiv reaktans

La oss se på et eksempel på hvordan du beregner den kapasitive reaktansen: Anta at en 6 μF kondensator er koblet til et vekslende strømuttak og frekvens og frekvens F 60 Hz.

For å finne den kapasitive reaktansen brukes definisjonen som er gitt i begynnelsen. Vinkelfrekvensen ω er gitt av:

Det kan tjene deg: Magnetisk induksjon: Formler, hvordan det beregnes og eksempler

Ω = 2πf = 2π x 60 Hz = 377 s^-1

Da erstattes dette resultatet i definisjonen:

X_C = 1 / ωc = 1 / (377 s^-1x 6 x10 ^-6 F) = 442.1 ohm

La oss nå se amplituden til strømmen som sirkulerer i kretsen. Siden kilden tilbyr en amplitudespenning V_C = 40 V, vi bruker forholdet mellom kapasitiv reaktans, strøm og spenning for å beregne amplituden til maksimal strøm eller strøm:

Yo_C = V_C / X_C = 40 v / 442.1 ohm = 0.09047 A = 90.5 m a.

Hvis frekvensen blir veldig stor, blir den kapasitive reaktansen liten, men hvis frekvensen ble 0 og vi hadde en likestrøm, ville reaktansen en tendens til å være uendelig.

Strøm og kondensatorspenning

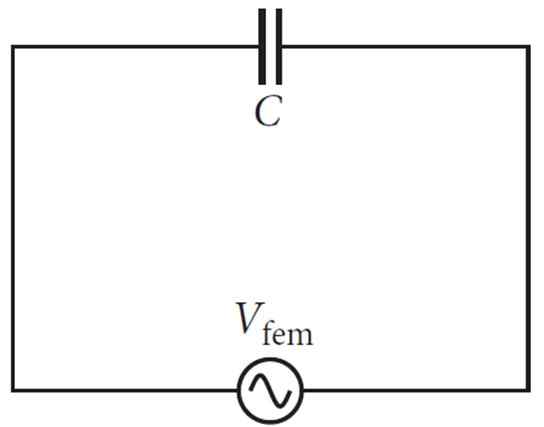
Når en kondensator kobles til en vekselstrømskilde, for eksempel den svinger og endrer polariteten, opplever kondensatoren belastninger og utslipp vekselvis.

For en frekvens på 60 Hz som eksemplet, er spenningen positiv 60 ganger per sekund, og negativ ytterligere 60 ganger per sekund.

Figur 2. Enkel kondensatorkrets og vekselstrømskilde. Kilde: f. Zapata.

Ved å øke spenningen, driver den strømmen i en retning, men hvis kondensatoren laster ned, skjer strøm i motsatt retning som motsetter seg den første.

Ja v_C (t) = v_m Sen ωt, vel vitende om at kapasiteten er årsaken mellom belastningen og spenningen, vil vi ha belastningen:

C = q/v → q (t) = cv = cv_m Sen ωt

Og å ha belastningen avhengig av tid, vi vil ha strømmen, som er derivatet av det:

Yo_C(t) = CV_m Ω cos ωt

Men bryst og kosinus er relatert til: cos α = sin (α + π/2), derfor:

Yo_C(t) = CV_m Ω sen (ωt + π/2) = i_C Sen (ωt + π/2)

Med jeg_C = CV_C Ω

Som det fremgår av, er det en forskjell på 90º fremgang for strømmen med hensyn til spenningen, som kommentert i begynnelsen.

Kan tjene deg: Millikan Eksperiment: Prosedyre, forklaring, betydning

I beskrivelsen av denne typen kretsløp, begrepet konseptet Fasor, som ligner mye på en vektor og lar representere i det komplekse planet enhver vekslende mengde som strøm, spenning eller impedans.

Følgende figur viser til høyre på spenningen og strømforsikringene i kondensatoren, som danner en vinkel på 90º, som er etterslepet mellom de to.

Til venstre er de respektive grafer, av forskjellige amplituder, men like frekvens. Med tiden går strømmen frem til spenningen, og når dette er maksimalt, er strømmen null, og når spenningen er null, er strømmen maksimal, men med den omvendte polariteten.

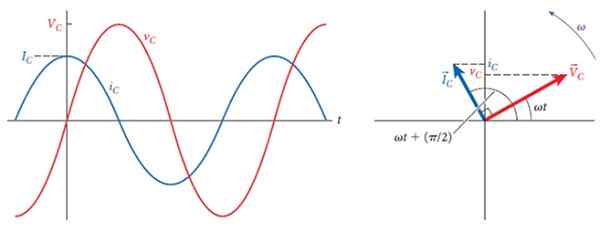Figur 3. 90º lag mellom strømmen og spenningen gjennom en kondensator. Kilde: Bauer, W.

Kompleks kondensatorimpedans

I en krets med motstander, kondensatorer og induktanser, er reaktans den imaginære delen av Z -impedansen, en kompleks mengde som i vekselstrømskretser har en rolle som ligner på elektrisk motstand for likestrøm de som er direkte strøm.

Faktisk er impedansen til en krets definert som årsaken mellom spenningen og strømmen:

Z = v / i

For en kondensator eller kondensator er dens impedans gitt av kvotienten:

Z_C = v (t) / i (t) = v_C Sen ωt / i_C Sen (ωt + π/2)

En måte å uttrykke spenning og strøm som Fasores er å indikere amplituden og fasevinkelen (polar form):

v (t) = v_C ∠ 0º

I (t) = i_C ∠ 90º

Derfor:

Z_C = V_C ∠ 0º / i_C ∠ 90º = (v_C / Yo_C) ∠ 0º -90º =

= V_C / CV_C Ω ∠ -90º = (1/ ωC) ∠ -90º =

Z_C = (- j) x_C

Det vil si at impedansen til kondensatoren er dens kapasitive reaktans multiplisert med den negative av den imaginære enheten.

Impedans av en serie RC -krets

Impedansen av en vekselstrømskrets med motstand, kondensatorer og induktorer kan også representeres binomialt av:

Det kan tjene deg: Første lov om termodynamikk: Formler, ligninger, eksempler

Z = r + jx

I denne ligningen representerer R motstanden, som tilsvarer den virkelige delen, J er den imaginære enheten og X er reaktansen, som kan være kapasitiv eller induktiv eller kombinasjon av begge deler, hvis disse elementene er til stede samtidig i kretsen.

Hvis kretsen inneholder en motstand og en seriell kondensator, er impedansen:

Z = z_R + Z_C    

Som i motstandsspenning og strøm er i fase, er resistiv impedans ganske enkelt verdien av motstand r.

Når det gjelder kapasitiv impedans, har vi allerede sett at Z_C = -Jx_C , Derfor er impedansen til RC -kretsen:

Z = r - jx_C = R - j (1/ ωc)

For eksempel i kretsen vist nedenfor, hvis kilde er av formen:

100 V ⋅ sen (120πt)

Observering av at ω = 120π, er impedansen:

Z = 83.0 - J [(1 / (120π ⋅ 6 x 10^-6)] ohm = 83.0 - 442.1 J ohm.

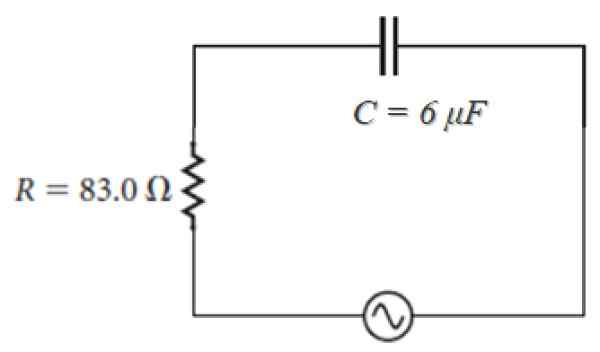Figur 4. RC Circuit Series med vekslende strømkilde. Kilde: f. Zapata.

Kapasitive reaktansapplikasjoner

PASA høye filtre, lavpassfilter, brokretser for å måle kapasitanser og induktanser og kjøleskapskretser er blant hovedkretsapplikasjonene som inneholder kapasitive reaktanser, i kombinasjon med induktanser og elektrisk motstand.

I lydutstyr har noen høyttalere med separate typer type Woofer (større) for lave frekvenser og Tweeter eller lite horn for høye frekvenser. På denne måten forbedres ytelsen og kvaliteten på lyden.

De brukes kondensatorer som forhindrer ankomst av lave frekvenser i tweeteren, mens en induktor legges til i wooferen for å unngå høyfrekvente signaler, siden induktansen har en reaktans proporsjonal med frekvensen: x x x_L = 2πfl.

Referanser

1. Alexander, ca. 2006. Elektriske kretsfundamenter. 3. Utgave. Mc Graw Hill.
2. Bauer, w. 2011. Fysikk for ingeniørfag og vitenskap. Volum 2. Mc Graw Hill.
3. Figueroa, d. 2005. Serier: Fysikk for vitenskap og ingeniørfag. Volum 6. Elektromagnetisme. Redigert av Douglas Figueroa (USB).
4. Giancoli, d.  2006. Fysikk: Prinsipper med applikasjoner. 6. Ed Prentice Hall.
5. Serway, r., Jewett, J. 2008. Fysikk for vitenskap og ingeniørfag. Volum 1. 7. Ed. Cengage Learning.