Hva er indre alternative vinkler? (Med øvelser)

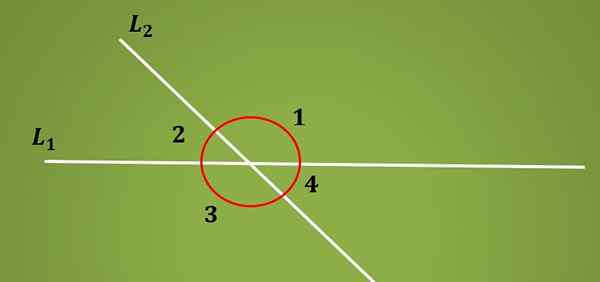
De Interne alternative vinkler De er de vinklene som er dannet av skjæringspunktet mellom to parallelle linjer og en tverrgående linje. Når en L1 -linje kuttes av en tverrgående linje, dannes L2 4 vinkler.

De to parene med vinkler som forblir på samme side av L1 -linjen kalles tilleggsvinkler, siden summen er lik 180º. I det nedre bildet er vinklene 1 og 2 supplerende, så vel som vinkler 3 og 4.

For å snakke om interne alternative vinkler, er det nødvendig å ha to parallelle linjer og en tverrgående linje; Som sett før vil det danne åtte vinkler.

Når det er to parallelle linjer L1 og L2 kuttet av en tverrgående linje, dannes åtte vinkler, som illustrert i følgende bilde.

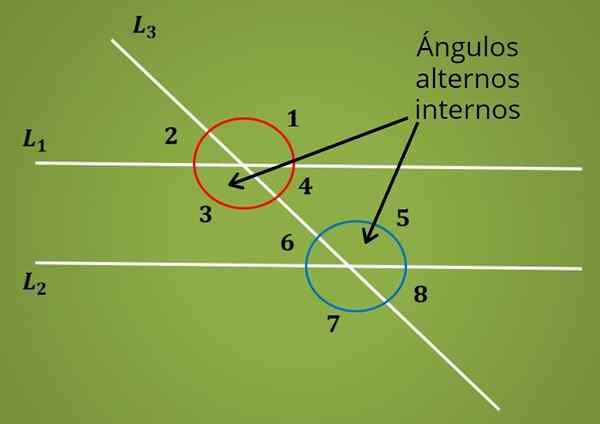
I det overordnede bildet er parene av vinkler 1 og 2, 3 og 4, 5 og 6, 7 og 8 supplerende vinkler. 

Nå er de indre alternative vinklene de mellom de to parallelle linjene L1 og L2, men er plassert på motsatte sider av den tverrgående linjen L2. Det er Vinkler 3 og 5 er indre alternativ. Tilsvarende er vinkler 4 og 6 indre alternative vinkler.

Motsatte vinkler av toppunktet

For å vite verktøyet som interne alternative vinkler har, er det først nødvendig å vite at hvis to vinkler blir motarbeidet av toppunktet, må disse to vinklene måler det samme.

For eksempel måler vinkler 1 og 3 det samme som de er motarbeidet av toppunktet. Under samme begrunnelse kan det konkluderes at vinklene 2 og 4, 5 og 7, 6 og 8 måler det samme.

Vinkler dannet mellom en sekant og to paralleller

Når det er to parallelle linjer kuttet av en tørr eller tverrgående linje som i forrige figur, er det sant at vinklene 1 og 5, 2 og 6, 3 og 7, 4 og 8 måler det samme.

Interne alternative vinkler

Ved å bruke definisjonen av vinkler plassert av toppunktet og egenskapen til vinklene som er dannet mellom en secant og to parallelle linjer, kan det konkluderes med at de interne alternative vinklene har samme tiltak.

Løste øvelser

- Første trening

Beregn målet på vinkel 6 i følgende bilde, vel vitende om at vinkel 1 måler 125º.

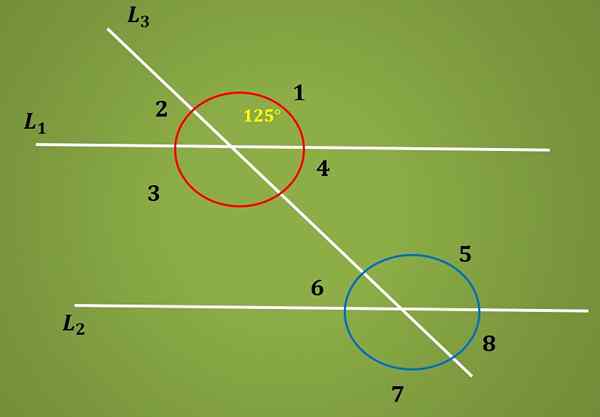
Løsning

Siden vinkler 1 og 5 er motsatt av toppunktet, har du den vinkelen 3 måler 125º. Nå, siden vinkler 3 og 5 er indre alternativ, har du at vinkelen 5 også måler 125º.

Til slutt, siden vinkler 5 og 6 er supplerende, er målet på vinkel 6 nødvendig lik 180º - 125º = 55º.

- Andre trening

Beregn vinkelen 3, vel vitende om at vinkel 6 måler 35º.

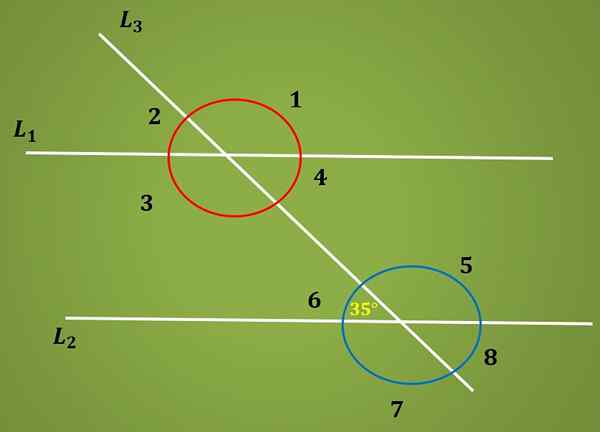
Løsning

Det er kjent at vinkel 6 måler 35º, og det er også kjent at vinkler 6 og 4 er indre alternativ, derfor måler de det samme. Det vil si at vinkel 4 måler 35º.

På den annen side, ved å bruke det faktum at vinkler 4 og 3 er supplerende, er målet på vinkel 3 lik 180º - 35º = 145º.

Observasjon

Det er nødvendig at linjene er parallelle slik at de kan oppfylle de tilsvarende egenskapene.

Øvelsene kan løses raskere, men denne artikkelen ønsket å bruke egenskapen til interne alternative vinkler.

Referanser

1. Bourke. (2007). En vinkel på geometri matematikkarbeidbok. NewPath Learning.
2. Clemens, s. R., O'Dafer, s. G., & Cooney, t. J. (1998). Geometri. Pearson Education.
3. Lang, s., & Murrow, G. (1988). Geometri: Et videregående kurs. Springer Science & Business Media.
4. Lira, a., Jaime, p., Chavez, m., Gallegos, m., & Rodríguez, C. (2006). Geometri og trigonometri. Umbrale utgaver.
5. Moyano, a. R., Saro, a. R., & Ruiz, r. M. (2007). Algebra og kvadratisk geometri. Netbiblo.
6. Sullivan, m. (1997). Trigonometri og analytisk geometri. Pearson Education.
7. Wingard-Enelson, r. (2012). Geometri. Enslow Publishers, Inc.