Konvergensradiodefinisjon, eksempler og øvelser løst

Han Konvergensradius av en serie krefter er radius for kretsen av konvergens som serien konvergerer. Denne sirkelen strekker seg fra verdien som avbryter basen til kreftene til den nærmeste singulariteten til funksjonen som er knyttet til serien.

All analytisk funksjon f (z) Det har assosiert en serie krefter rundt et ikke -singulært punkt, kalt Taylor Series:

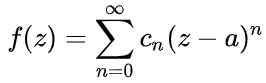
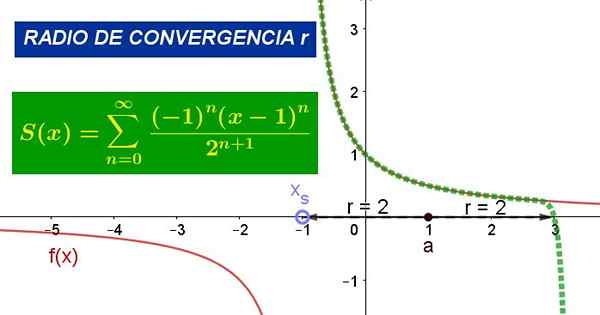
Figur 1. Grafen viser kraftserien rundt verdi a = 1 for funksjon f (x). Konvergensradius er r = 2. Kilde: Fanny Zapata.

Hvor til Det er sentrum av kretsen av konvergens, z den uavhengige variabelen til funksjonen og c_n De er koeffisienter relatert til de som er avledet fra funksjonen F på punktet z = a.

Konvergensradius r Det er et positivt reelt tall som definerer regionen:

| Z - A | < r

Der serien konvergerer. Ut av regionen Diverge -serien, det vil si at det tar uendelige verdier. Når konvergensradius er uendelig, konvergerer serien i hele det komplekse planet.

[TOC]

Hvordan bestemmes konvergensradius?

For at en serie skal være konvergent, er det nødvendig at den absolutte verdien av de påfølgende vilkårene vil avta når antallet vilkår er veldig stort. På matematisk måte vil det bli uttrykt som følger:

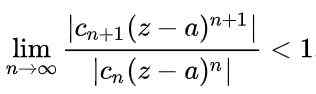
Ved å bruke egenskapene til grensene i forrige uttrykk, oppnås det:

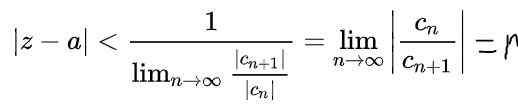
Her r Det er konvergensradius og | Z - A | < r Det er den åpne grensekretsen i det komplekse planet der serien konvergerer. I tilfelle verdien til Og variabelen Z er reelle tall, da vil det åpne intervallet for konvergens på den virkelige aksen være: (A - R, A+R).

Taylor Series

Taylor -serien med en funksjon f (x) Rundt en verdi til Der funksjonen har uendelige derivater, er det en serie krefter som er definert som:

Det kan tjene deg: aksiomer av sannsynlighet: typer, forklaring, eksempler, øvelser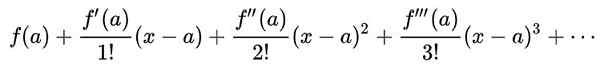

I miljøet | X - A | < r, med r somKonvergensradiusen til serien, Taylor -serien og funksjonen må være f (x) De sammenfaller.

På den annen side konvergensradius r Det er avstanden til punktet til og singulariteten x_s Nærmere poenget til, Å være entallpunktene de verdiene der funksjonens grense har en tendens til uendelig.

Det vil si når x → x_s så F → ± ∞.

Eksempler

Eksempel 1

Være S (x) Kreftene gitt av følgende uttrykk:

S (x) = 1 - x + x²- x³+ x⁴-.. .+(-1)ⁿ ⋅ xⁿ +.. .

For å bestemme regionen der serien konvergerer, beregner vi kvotienten mellom begrepet (n-beeimo + 1) og begrepet (n-EME):

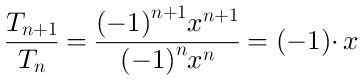
Den absolutte verdien av den fremre kvotienten er | x | og grensen når N → ∞ det er også  | x |.

For at serien skal være konvergent, er det nødvendig at:

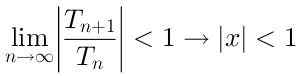
Så konvergensradiusen til denne serien er R = 1, Siden det konvergerer for verdiene til X som er på avstand mindre enn 1 med hensyn til sentrum x = 0.

Eksempel 2

Du vil finne Taylor -serien til funksjonen f (x) = 1 / (1 + x) rundt punktet x = 0 og bestemme dens konvergensradius.

For å finne serien tar vi de påfølgende derivater av funksjonen f (x), hvorav vi vil vise de tre første:

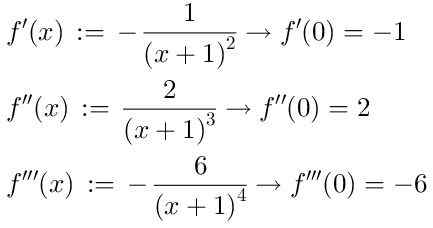
Tatt i betraktning at nullbestillingsperioden i Taylor -serien er:

 f (0) = 1,

Den første ordren: F '(0)/1!

Andre bestilling:

 F "(0)/2!

Tredje ordre:

 f "(0)/3!

Og så videre er Taylor -serien til den gitte funksjonen:

f (x) = 1 - x + x² - x³ + x⁴ -.. .+(-1)ⁿ ⋅ xⁿ +.. .

Kan tjene deg: likesidt trekant: egenskaper, egenskaper, formler, område

Som sammenfaller med kraftserien som er studert i eksempel 1.

Vi har allerede sagt at konvergensradiusen til en Taylor -serie er avstanden fra sentrum av utvidelsen i serie, som i vårt tilfelle er verdien x = 0 til funksjonens første singularitet f (x). 

Ettersom vår funksjon har en singularitet (det vil si en uendelig) i x = -1, Avstanden mellom verdien -1 og utvidelsessenteret 0 er | -1 - 0 | = 1, Det er konkludert med at konvergensradius fra Taylor Series er 1.

Dette resultatet sammenfaller fullt sammen med det som er oppnådd i eksempel 1 på en annen metode.

At Taylor Series Convergence Zone er det åpne intervallet (-1, 1) innebærer at funksjonen og serien sammenfaller i dette intervallet, men ikke utenfor det samme.

Som er vist i figur 2, der 41 vilkår i Taylor -serien er tatt, tegnet av den kontinuerlige blå linjen, mens den opprinnelige funksjonen er vist på den røde segmenter.

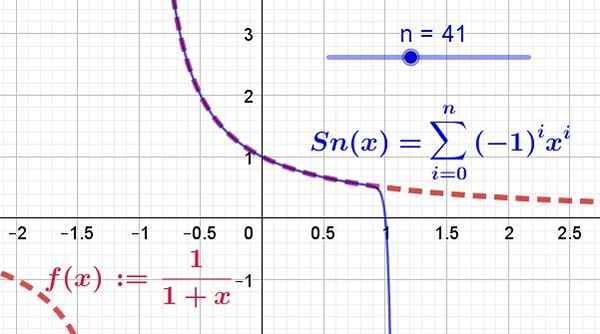Figur 2. Funksjonen f (x) (i rødt) og dens krefter (eller Taylor -serien i blått) vises. Det kan sees på som de første 41 begrepene i serien konvergerer mellom -1 og 1. I tillegg sammenfaller funksjonen og serien bare i konvergensregionen. (Kilde: Fanny Zapata)

Løste øvelser

- Oppgave 1

Tenk på den samme funksjonen f (x) = 1 / (1 + x) av eksempel 2, men denne gangen blir det bedt om å finne Taylor -serien med nevnte funksjon rundt punktet A = 1.

Løsning

Vi finner de påfølgende vilkårene i serien, som starter med det uavhengige begrepet som er f (1) = ½.

Den neste koeffisienten som tilsvarer den første ordensperioden er:

F '(1)/1! = -¼

Den andre ordren er:

f "(1)/2! = 2/(2³ 2!)

Følg tredje ordens koeffisient:

Det kan tjene deg: tetradecágon

f "(1)/3! = -6 / (2⁴ 3!)

Og så videre. Taylor -serien vil være:

Sf (x) = ½ - 1/2² (X-1) + 1/2³(X-1)² - 1/2⁴ (X-1)³ + 1/2⁵ (X-1)⁴-..

- Oppgave 2

Finn konvergensradiusen til forrige serie

Løsning

Vi skriver begrepet n-eme og begrepet n-alkaus mer en:

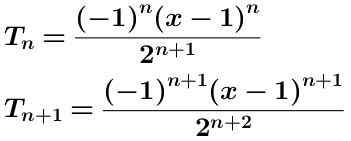Vi beregner kvotienten til disse to begrepene som er vist nedenfor forenklet:

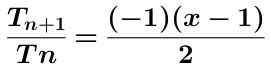
Den absolutte verdien av det forrige uttrykket tas ved å oppnå:

| X - 1 | / 2

For at serien skal være konvergent, er det imidlertid nødvendig at det forrige beløpet er strengt lavere enn enheten, det vil si:

| X - 1 | < 2

Som indikerer at konvergensradius rundt verdien x = 1 er:

R = 1

På den annen side tilsvarer det forrige uttrykket dobbelt ulikhet:

-2 < x - 1 < +2

Hvis vi legger til +1 til hvert av de tre medlemmene av det forrige uttrykket, oppnås det:

-1 < x < 3

Som er seriekonvergensintervall.

Figur 1 viser den opprinnelige funksjonen og Taylor -serien med nevnte funksjon rundt punkt x = 1. I figuren kan det verifiseres at serien sammenfaller med funksjonen i et miljø med punkt x = 1, men innenfor konvergensradius.

Referanser

1. CK-12 Foundation. Power Series: Representasjon av funksjoner og operasjoner. Gjenopprettet fra: CK12.org.
2. Engler, a. 2019. Integrert beregning. National University of the Coast.
3. Larson, r. 2010. Beregning av en variabel. 9na. Utgave. McGraw Hill.
4. Gratis matematikkekster. Power Series. Gjenopprettet fra: Matematikk.Liibretexts.org.
5. Wikipedia. Power Series. Gjenopprettet fra: er.Wikipedia.org.
6. Wikipedia. Konvergensradius. Hentet fra: i.Wikipedia.org