Grunn til å endre seg

Hva er grunnen til endring?

De grunn til å endre seg Det er den matematiske størrelsen som definerer endringen av en variabel eller av en fysisk størrelse angående en annen. For eksempel er hastighet årsaken til å endre posisjonen med hensyn til tiden.

En endring i en styrke x, Det er betegnet med de greske tekstene Δ (den lyder “Delta”) og er skrevet Δx. Det beregnes av forskjellen mellom en endelig og en startverdi: Δx = x_endelig- x_første.

Hvis størrelsen x er relatert til en annen størrelse og, Dette opplever også en endring, kalt Δy = y_endelig- og_første, Årsaken til å endre y med hensyn til x er definert som kvotienten:

Som ved å bruke notasjonen med Delta angitt før, forblir slik:

Denne kvotienten er kjent som Øk kvotienten av og med respekt for x enten gjennomsnittlig eller gjennomsnittlig endringsforhold.

På denne måten kan du definere størrelser som vekstindeksen til en befolkning, hastighet som et objekt, arbeidsledighet, vannstrømmen gjennom et rør og mange flere. Alle disse beløpene er i virkeligheten.

Hvorfor er det viktig å beregne årsaken til endring?

Tallrike størrelser av interesse forblir ikke uforanderlige, men opplever endringer, og ofte følger disse endringene hverandre i tide. Derfor viktigheten av å beregne årsaken til å endre en styrke over tid.

For eksempel er det det enkle tilfellet med et objekt som beveger seg langs en rett linje, som kan være den horisontale aksen eller aksen til x. Mobilen (en bil, en sykkel, en person som går eller løper ...) endrer kontinuerlig posisjon når tiden går t.

Deretter er grunnen til å endre plasseringen av objektet Δx i tidsintervallet ΔT, kjent som gjennomsnittshastighet:

En annen mobil som reiser gjennom den samme rette linjen kan gjøre det med forskjellig hastighet, enten eller mindre, og på denne måten skiller den seg fra den første mobilen (fordi den er tregere eller raskere).

For eksempel vil en 100 -meter flat korridor ha en gjennomsnittlig valutakurs i sin posisjon mye større enn en maratoner eller en person som går stille nedover gaten.

Hastighet er et typisk eksempel på endringsforhold, men noen interessante størrelser som også opplever endringer i tid, er: temperaturen, volumet av en væske, den elektriske ladningen, en populasjon av bakterier og mange flere.

Når du kjenner til grunnen til endring, kan du vite mye om måten disse størrelsene utvikler seg over tid.

Enheter av årsaken til endring

Forholdet er forholdet mellom to størrelser, de resulterende enhetene vil også være kvotienten til enhetene som brukes til å måle dem. For eksempel er hastigheten lengde mellom tiden, siden det er grunnen til å endre posisjonen med hensyn til tiden.

På denne måten kan hastighetsenhetene være meter/sekund, kilometer/time, miles/time og mange andre kombinasjoner.

Hvordan beregnes endringsgrunnen?

Gjennomsnittlig årsak eller valutakurs mellom to størrelser beregnes lett, når du utfører kvotienten mellom de respektive variasjonene til hver enkelt, i henhold til formelen:

Endringer i størrelser kan gis gjennom lagerbord eller bestemmes av en graf, hvorav de respektive verdiene til og og x (Se øvelsene løst på slutten).

På den andre siden:

Og uttrykk for høyre er nettopp hellingen på en linje, hvorav det konkluderes med at den gjennomsnittlige årsaken til endring er skråningen på sekantlinjen til grafen til y avhengig av x.

Tegn på årsaken til endring

I henhold til den gitte definisjonen kan årsaken til endring være positiv eller negativ, avhengig av hvordan størrelsene involvert varierer, siden disse kan øke eller avta, ifølge.

Hvis årsaken til endring er positiv, betyr det at endringer i og og i x De var det samme tegnet, det vil si, og økt og x Det gjorde han også. Eller så mye og som x De reduserte.

Men når årsaken til endring er negativ, betyr det at en av størrelsene økte og den andre reduserte.

Øyeblikkelig endring grunn

Ofte er det mye mer interessant. I dette tilfellet er det nødvendig å få Δx -variasjonen til å være ekstremt liten, og har en tendens til 0 (men uten å bli 0, siden divisjonen mellom 0 ikke er definert).

Dette kalles "å ta grensen", og i så fall kalles forholdet mellom øyeblikkelig endring "derivatet" av og med respekt for x og det er betegnet som dy/dx; Så:

Forholdet eller øyeblikkelig endringshastighet tilsvarer også skråningen på en linje, men i dette tilfellet er det skråningen på tangentlinjen til grafen til og mot x.

Enkle eksempler

En persons vekst

Siden de er født, vokser barn i et tempo bestemt av flere faktorer, blant dem genetikk og mat skiller seg ut. De høyeste vekstratene oppstår i løpet av det første leveåret; Senere, i løpet av barndommen og deretter i puberteten, opplever barn normalt "strekker", det vil si årsaken til endringen av høyden med hensyn til tid, og deretter redusere.

Etter puberteten fortsetter guttene å vokse, men frekvensen avtar til de blir kansellert, når de når sin definitive status av voksne.

Kaffe kult

Det er et kjent faktum at kaffe eller varm suppe gradvis avkjøles når den blir liggende ved romtemperatur. Imidlertid bremser kjølehastigheten nærmere kaffetemperaturen eller suppen ved romtemperatur.

En måte å modellere dette fenomenet er gjennom Newton kjølelov, i henhold til hvilken, hastigheten som varmen overføres er proporsjonal med forskjellen mellom temperaturen på stoffet og omgivelsestemperaturen. Proporsjonalitetskonstanten k er karakteristisk for stoffet:

T_enten representerer miljøtemperaturen.

Løste øvelser

Oppgave 1

Beregne det gjennomsnittlige endringsforholdet på og med respekt for x, Gitt følgende verdier:

og₁ = 3; og₂ = 10; x₁ = 2; x₂ = 5

Løsning

I henhold til formelen:

Verdiene gitt i uttalelsen erstattes og operasjonen blir løst:

Oppgave 2

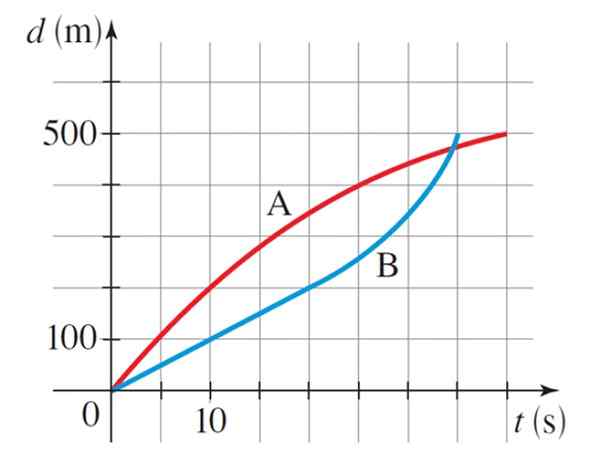
Grafen viser de respektive avstandskurvene kontra tid for to olympiske hurtigløpere A og B, i 500 meter modalitet. Som vant løpet? Hva var gjennomsnittlig hastighet for hver skater?

Løsning

Å observere grafen, følger det at Skater B (Blue Curve) vant løpet, siden det turnerte 500 m på 35 s, mens skater A (rød kurve), gjorde det på 40 s.

De respektive gjennomsnittshastighetene var:

Referanser

1. Figueroa, d. (2005). Serier: Fysikk for vitenskap og ingeniørfag. Volum 1. Kinematikk. Redigert av Douglas Figueroa (USB).
2. Glencoe Science. Endring og skråning (2021). Gjenopprettet fra: Glencoe.com.
3. Larson, r. (2012). Forkalkning. 8. Utgave. Cengage Learning.
4. Larson, r. (1986). Beregning med analytisk geometri, 2. Utgave. McGraw-Hill.
5. Stewart, J. (2011). College algebra, konsepter og kontekster. Brooks/Cole.