Reduksjon av lignende vilkår

Hva er reduksjon av lignende vilkår?

De Reduksjon av lignende vilkår Det er en metode som brukes til å forenkle algebraiske uttrykk. I et algebraisk uttrykk er de lignende begrepene de som har samme variabel; det vil si at de har de samme ukjente representert med et brev, og de har de samme eksponentene.

I noen tilfeller er polynomene omfattende, og for å nå en løsning må du prøve å redusere uttrykket; Det er mulig når det er vilkår som er like, som kan kombineres ved å bruke algebraiske operasjoner og egenskaper som sum, subtraksjon, multiplikasjon og inndeling.

Forklaring

De lignende begrepene dannes av de samme variablene med de samme eksponentene, og i noen tilfeller er disse bare forskjellige fra deres numeriske koeffisienter.

De som ikke har noen variabler, anses også som lignende vilkår; det vil si de begrepene som bare har konstanter. Dermed er for eksempel følgende lignende vilkår:

• 6x² - 3x². Begge begrepene har samme variabel x².
• 4. plass²b³ + 2²b³. Begge begrepene har de samme variablene til²b³.
• 7 - 6. Begrepene er konstante.

Disse begrepene som har de samme variablene, men med forskjellige eksponenter kalles ikke -limariske begreper, for eksempel:

• 9²B + 5AB. Variablene har forskjellige eksponenter.
• 5x + og. Variablene er forskjellige.
• B - 8. Det ene begrepet har en variabel, det andre er en konstant.

Identifisere de lignende begrepene som danner et polynom, kan disse reduseres til en, og kombinerer alle de som har de samme variablene med like eksponenter. På denne måten blir uttrykket forenklet ved å redusere antall vilkår som komponerer det, og beregningen av løsningen blir tilrettelagt.

Hvordan gjøre en reduksjon av lignende vilkår?

Reduksjon av lignende vilkår gjøres ved å anvende den tilknyttede egenskapen til produktets tillegg og distribusjonsegenskap. Ved hjelp av følgende prosedyre kan en reduksjon av vilkår gjøres:

• Først er lignende begreper gruppert sammen.
• Koeffisientene (tallene som følger med variablene) av de lignende begrepene blir lagt til eller trukket fra, og de assosiative, kommutative eller distribusjonsegenskapene brukes, som tilfellet kan være.
• Deretter er de nye vilkårene skrevet, og plasserer seg foran dem tegnet som ble resultatet av operasjonen.

Kan tjene deg: diskret matematikk

Eksempel

Reduser vilkårene for følgende uttrykk: 10x + 3y + 4x + 5y.

Løsning

Først blir vilkårene beordret til å gruppere de som er like, og anvende den kommutative eiendommen:

10x + 3y + 4x + 5y = 10x + 4x + 3y + 5y.

Deretter blir distribusjonseiendommen brukt og koeffisientene som følger med variablene legges til for å oppnå reduksjon av vilkårene:

10x + 4x + 3y + 5y

= (10 + 4) x + (3 + 5) og

= 14x + 8y.

For å redusere lignende vilkår er det viktig å ta hensyn til skiltene som har koeffisientene som følger med variabelen. Det er tre mulige tilfeller:

Reduksjon av lignende vilkår med like tegn

I dette tilfellet blir koeffisientene lagt til og foran resultatet er tegn på vilkårene plassert. Derfor, hvis de er positive, vil de resulterende begrepene være positive; I tilfelle begrepene er negative, vil resultatet ha tegnet (-) ledsaget av variabelen. For eksempel:

a) 22ab² + 12ab² = 34 AB².

b) -18x³ - 9x³ - 6 = -27x³ - 6.

Reduksjon av lignende begrep CPå forskjellige tegn

I dette tilfellet blir koeffisientene trukket fra, og foran resultatet er tegnet på hovedkoeffisienten plassert. For eksempel:

a) 15x²og - 4x²og + 6x²og - 11x²og

= (15x²og + 6x²Y) + ( - 4x²og - 11x²og)

= 21x²Y + (-15x²og)

= 21x²og - 15x²og

= 6x²og.

b) -5a³B + 3 a³B - 4A³b + a³b

= (3 a³b + a³b) + (-5a³B - 4A³b)

= 4a³B - 9a³b

= -5 a³b.

På denne måten, for å redusere de lignende begrepene som har forskjellige tegn, dannes et enkelt additive begrep med alle de som har et positivt tegn (+), blir koeffisientene lagt til og resultatet er ledsaget av variablene.

Det kan tjene deg: Unitary Circle: Trigonometric Functions and Applications

På samme måte dannes et subtraktivt begrep, med alle de begrepene som har et negativt tegn (-), blir koeffisientene lagt til og resultatet er ledsaget av variablene.

Til slutt trekkes summen av de to vilkårene som dannes, og tegnet på det største er plassert til resultatet.

Reduksjon av lignende vilkår i driften

Reduksjon av lignende vilkår er en algebraoperasjon, som kan brukes i sum, subtraksjon, multiplikasjon og algebraisk inndeling.

I summer

Når du har flere polynomer med lignende vilkår, for å redusere dem, bestilles vilkårene for hvert polynom å holde sine tegn, så blir de skrevet etter andre og de lignende vilkårene er redusert. For eksempel har du følgende polynomer:

3x - 4xy + 7x²og + 5xy².

- 6x²og - 2xy + 9 xy² - 8x.

I subtraksjoner

For å trekke fra et polynom fra et annet, blir minuenden skrevet og trekker det deretter med sine endrede tegn, og deretter blir reduksjon av lignende vilkår gjort. For eksempel:

5. plass³ - 3ab² + 3b²c

6ab² + 2³ - 8b²c

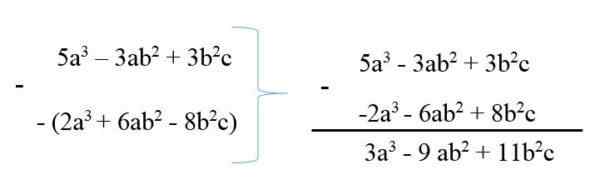
Dermed blir polynomer oppsummert ved 3A³ - 9ab² + 11b²c.

I multiplikasjoner

I et polynomprodukt er begrepene som utgjør multipliseringen for hvert begrep som danner multiplikatoren, med tanke på at tegnene på multiplikasjonen forblir de samme hvis disse er positive hvis de er positive.

De vil bare bli endret når de multipliserer med et begrep som er negativt; Det vil si at når to vilkår av det samme skiltet multipliserer, vil resultatet være positivt (+), og når de har forskjellige tegn, vil resultatet være negativt (-).

For eksempel:

a) (a + b) _* (A + B)

= a² + Ab + ab + b²

= a² + 2ab+ b².

B) (A + B) _* (A - B)

= a² - AB + AB - B²

= a² - b².

drosje) _* (A - B)

= a² - AB - AB + B²

= a² - 2ab+ b².

I divisjoner

Når du vil redusere to polynomer gjennom en divisjon, må en tredje polynom.

Det kan tjene deg: Tukey Test: Det som er i tilfelle av eksempel løst trening

For det må vilkårene for utbyttet og divisoren bestilles, fra venstre mot høyre, slik at variablene i begge er i samme rekkefølge.

Divisjonen blir deretter utført, med start fra første periode av venstre for utbyttet mellom den første til venstre for divisoren, tar alltid hensyn til tegnene på hvert begrep.

Reduser for eksempel polynom: 10x⁴ - 48x³og + 51x²og² + 4xy³ - 15y⁴ Deling det mellom polynom: -5x² + 4xy + 3y².

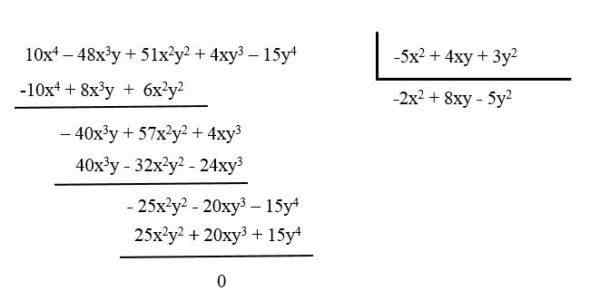
Det resulterende polynomet er -2x² + 8xy - 5y².

Løste øvelser

Første trening

Reduser vilkårene for det algebraiske uttrykket gitt:

15a² - 8AB + 6A² - 6ab - 9 +4a² - 13 AB.

Løsning

Summen til summen blir brukt, og grupperer begrepene som har de samme variablene:

15a² - 8AB + 6A² - 6ab + 9 + 4a² - 1. 3

= (15a² + 6² + 4. plass²) + ( - 8AB - 6AB) + (9 - 13).

Deretter brukes den distribuerende egenskapen til multiplikasjonen:

15a² - 8AB + 6A² - 6ab + 9 + 4a² - 1. 3

= (15 + 6 + 4) a² + ( - 8 - 6) AB + (9 - 13).

Til slutt blir de forenklet ved å legge til og trekke fra koeffisientene for hvert begrep:

15a² - 8AB + 6A² - 6ab + 9 + 4a² - 1. 3

= 25a² - 14AB - 4.

Andre trening

Forenkle produktet av følgende polynomer:

(8x³ + 7xy²)_*(8x³ - 7 xy²).

Løsning

Hver periode av det første polynomet multipliseres med det andre, under hensyntagen til at tegnene på begrepene er forskjellige; Derfor vil resultatet av multiplikasjonen være negativt, så vel som lovene til eksponentene må brukes.

(8x³ + 7xy²) _* (8x³ - 7xy²)

= 64 x⁶ - 56 x³_* Xy² + 56 x³_* Xy² - 49 x²og⁴

= 64 x⁶ - 49 x²og⁴.