Korrespondanse regel om en funksjon

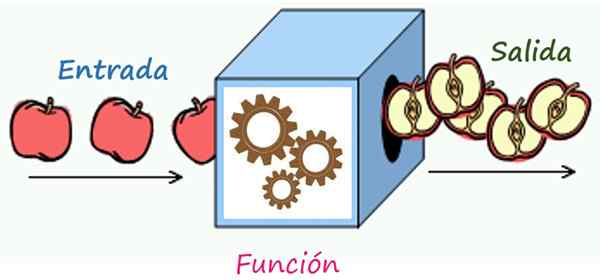
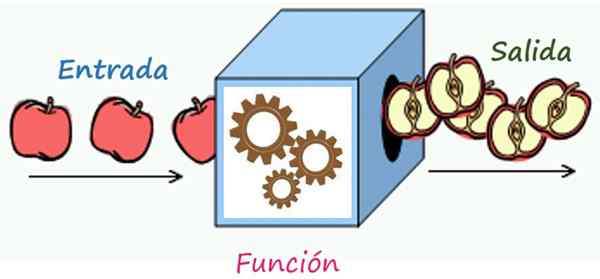Korrespondanseregelen er en mekanisme som forvandler elementene i inngangen til utgangselementene. Kilde: Wikimedia Commons/F. Zapata

Hva er korrespondanseregelen for en funksjon?

De Korrespondanse regel om en funksjon Påpeke måten elementene i ett sett er relatert til elementene i et annet. Elementene i det første settet er kjent som domene, og til de andre, som Codominium enten Conquominium.

Forholdet eller koblingen mellom sett kan spesifiseres av verbal eller skriftlig instruksjon, men når settene er numeriske, indikeres korrespondanseregelen med en formel.

Denne formelen inneholder operasjonene som må gjøres med elementene i startmonteringen, og dermed oppnå en serie elementer inkludert i Codominium.

Når forholdet mellom elementene er en funksjon, oppfyller korrespondanseregelen to spesielle forhold:

• Til hvert av elementene i domenet er tilknyttet, gjennom korrespondanseregelen, et enkelt element i codominium, kjent som bilde.
• Dette bildet er unikt, med andre ord, intet element i domenet er assosiert med mer enn ett element av codominium.

På denne måten kan du forestille deg korrespondanseregelen for en funksjon som en mekanisme låst i en boks. Hver domeneverdi, uten unntak, kan gå inn i boksen og komme ut av den transformert, gjennom operasjonene som er angitt med korrespondanseregelen. Eksemplene vil bli sett umiddelbart.

Eksempler

Eksempel 1

Korrespondanseregelen for en funksjon kan uttrykkes som en skriftlig instruksjon, når elementene ikke er numeriske.

For eksempel er det et sett med land, betegnet som P, og et annet sett med byer C:

Det kan tjene deg: U -est av Mann - Whitney: Hva er det og når du brukes, utførelse, eksempel

P = Canada, Mexico, Spania, USA, Frankrike, Argentina, Brasil, Tyskland

C = Paris, London, Buenos Aires, Berlin, Mexico City, Ottawa, Río, New York, Madrid, Washington, Bern, Roma, Brasilia, Toronto

Være korrespondanseregelen F Mellom P og C gitt av:

F: P → c

Hvor F Det er regelen "... hvis kapital er .. ”, Som forbinder hvert land i P (startsettet), med hovedstaden i C (ankomstsettet).

For eksempel: “Spania, hvis kapital er Madrid ". "Spania" -elementet tilhører startpsettet, og "Madrid" -elementet til hele C, ankomsten.

Representasjonen av denne funksjonen kan gjøres gjennom et Venn -diagram eller bare gjennom bestilte par.

Bestilte par inneholder, som navnet tilsier, to elementer med en spesifikk ordre, i dette eksemplet er det første elementet i paret landet, og det andre, hovedstaden.

For sin del er Venn -diagrammet en måte å visualisere funksjonen på, og viser start- og ankomstsettene, så vel som korrespondanse -regelen mellom dem.

Representasjon av f som bestilte par

F = (Canada, Ottawa); (Mexico, Mexico City); (Spania Madrid); (USA; Washington); (Paris, Frankrike); (Argentina Buenos Aires); (Brasil Brasilia); (Tyskland, Berlin)

Det første paret knytter Canada, hvis kapital er Ottawa, den andre knytter Mexico, hvis kapital er Mexico by og så videre.

Representasjon av F som et Venn -diagram

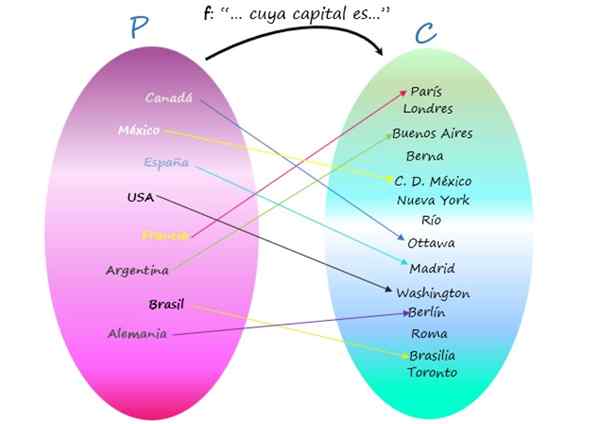
Merk at det er byer som ikke er hovedstaden i noe land, siden de, selv om de er elementer i Codominium, ikke er et bilde av noe element i startsettet. Likevel er forholdet en funksjon, fordi det viktige er at hvert land har sin kapital, og dette er unikt.

Kan tjene deg: Område for en vanlig og uregelmessig Pentagon: Hvordan det tas, øvelser

Undergruppen dannet av elementene i kodominiet som er et bilde av et element i domenet, kalles rekke eller funksjon av funksjonen. For eksempelet, ruten r av F er:

R = Paris, Buenos Aires, Mexico City, Ottawa, Madrid, Berlin, Washington, Brasilia

Det er verdt å spørre om et forhold mellom C og P kan etableres, der C blir startsettet og ankomst. Svaret er ja, men det ville ikke være en funksjon, fordi det er byer som ikke er hovedsteder, for eksempel New York, eller det landet de er hovedstad, vises ikke blant elementene i P -komplekset, for eksempel Roma.

Eksempel 2

Når avgangssettet og ankomstsettet er numerisk, er korrespondansen til funksjonen som kobler dem en formel. Vær for eksempel mestring av en funksjon Følgende sett:

D = 0, 1, 2, 3, 4, 5, 6)

Korrespondanse -regelen F: D → R som kobler elementene i D med settet med reelle tall r er:

F: "Dobbelt"

Hvis "x" er et element i startsettet, er F (x) det tilsvarende elementet i ankomstsettet, og korrespondanseregelen er skrevet slik:

f (x) = 2x

Codominium er settet med reelle tall. En delmengde av reais er ruten for denne funksjonen, settet med tall hvis verdi er dobbelt så x:

R = 0, 2, 4, 6, 8, 10, 12

I form av bestilte par resulterer korrespondanseregelen i:

F = (0,0); (1.2); (2,4); (3,6); (4.8); (5.10); (6,12)

Bestilte par kan være graf i det kartesiske flyet. Det første elementet i dreiemomentet er plassert på den horisontale aksen, også kalt Axis -aksen eller "X" -aksen, mens den andre går på den vertikale aksen, aksen til den bestilte eller ganske enkelt aksen "y":

Kan tjene deg: Distributive eiendommer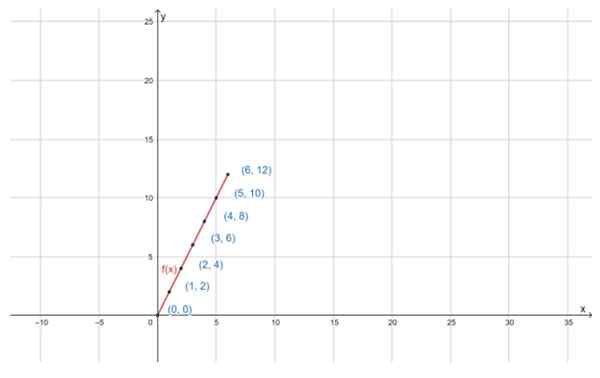 Grafen til funksjonen f (x) = 2x, for det spesifiserte D -domenet, er en rett linje. Kilde: f. Zapata gjennom Geogebra

Øvelser

Bestem korrespondanseregelen for følgende forhold, som indikerer om de er funksjoner eller ikke. Settet med naturlige tall er n og det av det virkelige er r.

Angi også domenet, codominium og funksjonens rute, i de tilfeller det tilsvarer:

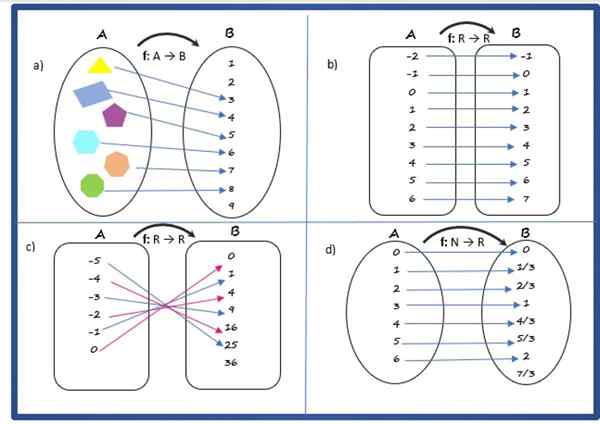
Løsning på

Det er en funksjon, siden hvert element i startsettet, bestående av polygoner, har et unikt bilde i ankomstsettet.

Korrespondanseregelen relaterer polygon til antall sider, domenet består av sett A for polygonene:

A = Triangle, Quadrilateral, Pentagon, Hexagon, Heptagon, Octagon

Codominium er settet med de første naturlige tallene, inkludert 0.

B = 0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Og CO C er de naturlige tallene fra 3 til 8:

C = 3, 4, 5, 6, 7, 8

Løsning b

Det er en funksjon, siden den oppfyller forholdene som er spesifisert ovenfor.

Korrespondensregelen er:

f (x) = x + 1

Korrespondanseregelen indikerer at funksjonen er definert av R → R, derfor er domenet settet med reelle tall. Og co -roominium og ruten faller også sammen med det virkelige.

Løsning c

Det er en funksjon, med korrespondanseregelen:

f (x) = x²

Domene og kodominium er sett med reais, men ruten består bare av positive reelle tall, betegnet som r⁺ og inkludert 0.

Løsning d

Det er en funksjon. Korrespondanseregelen er:

f (x) = x/3

Dens domene er settet med naturlige tall n og codominium, så vel som ruten, er de virkelige n -tallene r.