Spakregel

Hva er spakregelen?

De spakregel Det er en matematisk prosedyre som gjør det mulig. Ikke bare er det matematisk, men også ganske grafisk og selvsikker, og er veldig nyttig i fysisk -kjemiske og ingeniørberegninger.

Denne regelen gjelder fasediagrammer for binære systemer, uavhengig av typen system selv. Det vil si at fasene kan være solide, som med legeringene; eller væske og gassformig, som vi ser i systemer i likevekt.

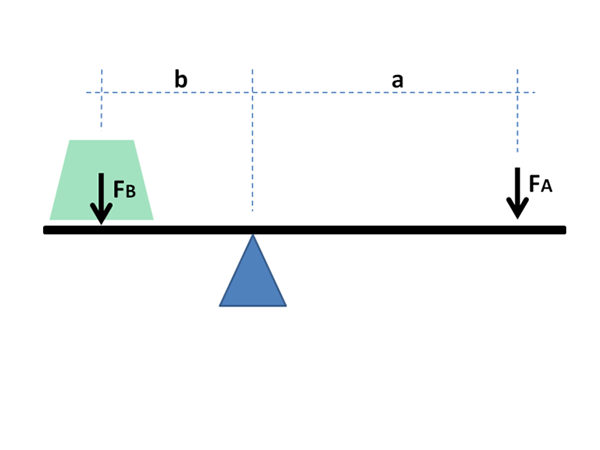
Spakens fysiske og matematiske prinsipp brukes også til kjemiske formål og i fysikken i materialene. Kilde: Jimbowley, CC BY-SA 3.0, via Wikimedia Commons

Spakregelen kan brukes direkte å ta hensyn til verdiene grafikken i Abscissa -aksen, der de globale brøkene eller prosentene av den mest flyktige komponenten vanligvis går, i tilfelle av væsker; eller ildfast, i tilfelle av metaller i legeringene sine.

Som det fremgår nedenfor, skyldes navnet den enorme likheten det har med de matematiske uttrykkene som demonstrerer balansen mellom to masser som ligger i endene av en rocker med Fulcro.

Spakarmene må balansere for å balansere massene på belastningen; Når det.

Forklaring

Grafiske aspekter

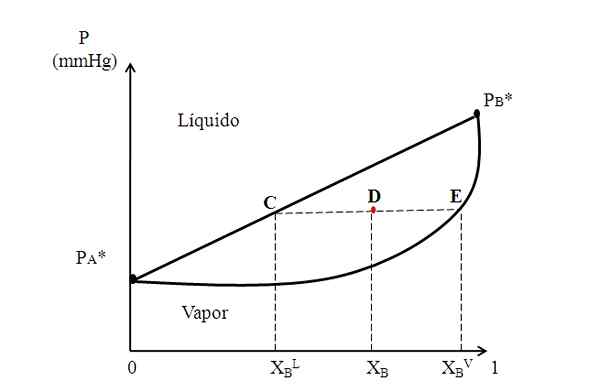Hypotetisk binært diagram der en bindingslinje viser sammensetningene av væske- og dampfasene. Kilde: Gabriel Bolívar.

Midt i diagrammet over har vi et område der væske og damp sameksisterer; Det vil si at væskedamper-likevektsområdet. Over dette området vil blandingen av A og B være flytende, og under vil det være brus på grunn av det nedre trykket.

Vurder nå en blanding med en X -komposisjon_B og hvis trykk plasserer det på punkt D. Vi trekker fra punkt D en horisontal linje som berører linjen og kurven på sidene, opprinnelige punkter C og E,. Denne linjen, som kommuniserer punkter C, D og E, C-D-E, er den som er kjent som Union Line, og ved å projisere den mot aksen og må gi oss presset fra systemet.

Det kan tjene deg: vannkalinitet: hva er, besluttsomhet og betydning

Så, fra disse punktene, trekker vi andre linjer vinkelrett på bindingslinjen, som vil spille X -aksen. Når punkt E hviler på dampkurven, vil vi ha den molære fraksjonen av B i dampfasen (x_B^V). På samme måte vil punkt C, på den rette væskelinjen, gi oss den molære fraksjonen av B i væskefasen (x_B^L).

Spakregelen er nettopp basert på bindingslinjen, og avstandene mellom x_B^L, X_B og x_B^V.

Matematisk fradrag

Den globale molære brøkdelen av B er lik:

X_B = n_B / (n^L + n^V)

Hvor n_B De er de totale molene av B både i væske- og dampfasen, og n^L og n^V er de respektive føflekkene for disse fasene. Lysning n_B vi vil ha:

n_B = X_Bn^L + X_Bn^V (1)

På den andre siden, n_B Det er også lik:

n_B = n_B^L + n_B^V

= X_B^Ln^L + X_B^Vn^V  (2)

Nå vil utjevning av ligninger (1) og (2) gi oss:

X_Bn^L + X_Bn^V = X_B^Ln^L + X_B^Vn^V

Og omorganisere:

n^L(X_B - X_B^L) = n^V(X_B^V - X_B) (3)

n^L(C-d) = n^V(AV)

Disse to siste matematiske uttrykkene er spakregelen. Merk at x_B - X_B^L Det er avstanden mellom punktene C og D; og x_B^V - X_B, Det er avstanden mellom punktene D-E: de to halvdelene av bindingslinjen (spakarmene).

Denne ligningen er veldig lik den som beskriver massenes balanse på en rocker med bulcro:

m₁l₁ = m₂l₂

Dermed vil spakregelen tillate oss å beregne de totale molene n^L og n^V forutsatt at de totale molene av blandingen er kjent, n_T (n_T = n^L + n^V).

Andre form

Det forrige uttrykket for spakregelen tjener til å beregne mengder (masser, føflekker osv.) av fasene i likevekt. Den mest kjente versjonen av spakregelen lar oss imidlertid beregne brøkene eller prosentene i hver fase, og tar bare avstandene mellom x_B, X_B^L og x_B^V.

Tenk på det samme systemet ovenfor, med en annen form for spakregelen:

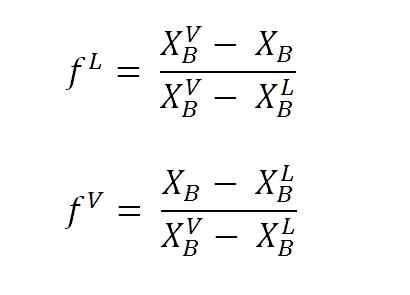Ligninger for å beregne væske- og dampfraksjoner ved bruk av spakarmene. Kilde: Gabriel Bolívar.

Hvor F ^L og F ^VDe er molære fraksjoner (eller prosent, avhengig av grafen) av henholdsvis væske- og dampfaser. Legg merke til at åpenbart, F ^L og F ^V De har ingen enheter; samtidig som n^L og n^V Ja de har enheter (føflekker, gram osv.).

Kan tjene deg: reaksjonsvarme

Eksempler

Metode 1

I en beholder 28 mol B og 12 mol av A er blandet. Bestem mengdene og molære fraksjoner for fasene som dannes.

Vi beregner x_B:

X_B = (28 føflekker b)/ (28 føflekker b + 12 mol a)

= 0.7

Denne verdien tilsvarer x_B av toppdiagrammet. Avskjæringen vil gi oss omtrent følgende verdier for x_B^L og x_B^V:

X_B^L = 0.41

X_B^V = 0.94

Med spakregelen:

n^L(X_B - X_B^L) = n^V(X_B^V - X_B)

Og å vite det n_T = n^L + n^V, og? n_T = 40 føflekker, så rydder vi n^L enten n^V Avhengig av den andre:

n^L(X_B - X_B^L) = (40 føflekker - n^L) (X_B^V - X_B)

Omorganisere og rydde n^L vi vil ha:

n^L = (40 føflekker) (x_B^V - X_B) / (X_B^V - X_B^L)

Husker ikke dette uttrykket det av F ^L? Nå erstatter vi:

n^L = (40 føflekker) (0.94 - 0.70) / (0.94 - 0.41)

= 18.11 mol i flytende fase

Vi kan beregne n^V På to måter:

n^V = n^L(X_B - X_B^L) / (X_B^V - X_B)

enten

n^V = 40 føflekker - 18.11 føflekker

= 21.89 føflekker i dampfase

Metode 2

Hva om vi beregner først F ^L og F ^V?

F ^L = (X_B^V - X_B) / (X_B^V - X_B^L)

= (0.94 - 0.70) / (0.94 - 0.41)

= 0.4528 eller 45.28%

Det vil si 45.2% av føflekkene er i en flytende fase, og er den mengden lik:

n^L = F ^Ln_T

= (0.4528) (40 føflekker)

= 18.11 føflekker

OG F ^V Vi kan beregne det likt på to måter:

F ^V = 1 - F ^L

enten

F ^V = (X_B - X_B^L) / (X_B^V - X_B^L)

Å være dens verdi:

F ^V = 0.5472 eller 54.72%

Og derfor, n^V Det vil være lik:

n^V = F ^Vn_T

= (0.5472) (40 føflekker)

= 21.89 føflekker

Merk at bruk av de to formene for spakregelen som alternative beregningsmetoder, de samme resultatene kan nås. Metode 2 virker mer direkte og enkel; Men hvis det blir observert nøye, når lysingen er løst n^L enten n^V, Det vil sees at begge metodene faktisk er like enkle.

Løste øvelser

Deretter vil to andre øvelser bli løst, hvor systemene som vurderes nå vil innebære en væske-fast og ikke-væske-damp. Diagrammene er også grafiske med hensyn til systemtemperaturen og ikke deres trykk.

Oppgave 1

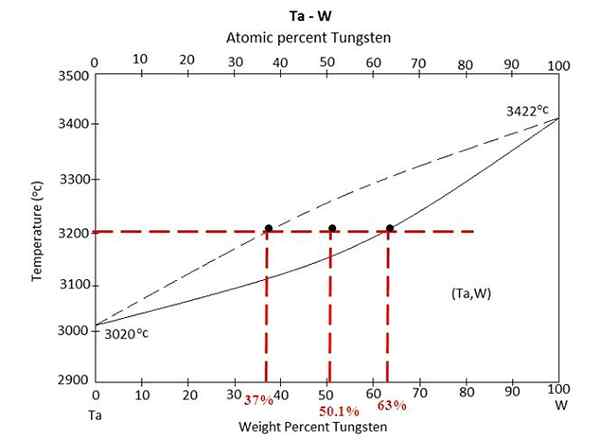Fasediagram for en legering mellom Tantalo og wolfram. Kilde: MaterialsPedia, CC BY-SA 4.0, via Wikimedia Commons

Vi har fasediagrammet over en legering mellom Tantalo og wolfram, ta-w. På x -aksen er de globale masseprosentene av wolfram, w% (m/m) representert.

Innenfor flytende likevektsområdet (TA+W) og fast stoff (legering) er det en blanding ved 3200 ºC. Bestem massene i hver fase forutsatt at 100 gram legeringen ble oppvarmet.

Det kan tjene deg: metaller, ikke -metaller og metalloider

Fremgangsmåte

Denne gangen vil øvelsen løses ved å bruke den andre formen for spakregelen. Unionslinjen forteller oss at: i den faste fasen har vi 63% av wolfram, mens vi i væskefasen har 37% wolfram. Dette er fordi wolframen smelter til en høyere temperatur (3422 ºC) enn tantal (3020 ºC).

Så vi har:

W%^S eller w_S= 63%

W%^L eller w_L= 37%

Og også:

W₀ = 50.1%

Vi bruker spakregelen på F ^L:

F ^L = (63% - 50.1%) / (63% - 37%)

= 0.4961 eller 49.61%

Merk at avstanden som tilsvarer væskefasen er spakarmen nær den faste fasen, motsatt side av mediumpunktet.

Massen i væskefasen er derfor:

(0.4961) (100 gram) = 49.61 smeltede gram

Og den faste fasen vil være lik:

100 gram - 49.61 gram = 50.39 gram legering rik på wolfram

Oppgave 2

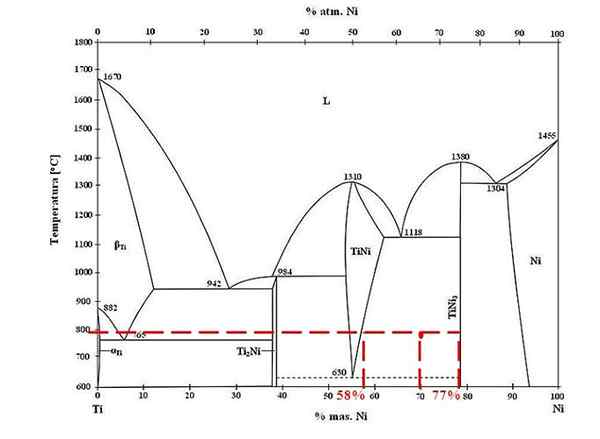Fasediagram for titan-nikkellegeringer. Kilde: Doomgiver, CC BY-SA 3.0, via Wikimedia Commons

For titan- og nikkellegering ved 800 ºC, og med 70% nikkel, bestemme hvor mye av Tini og Tini₃ De er til stede.

Fremgangsmåte

Denne gangen ber de bare om massefraksjonene i hver fase. Det røde punktet ligger i likevektsområdet mellom Tini- og Tini -fasene₃, hvis kurver er der den spiller faglinjen som flyter til verdiene 58% eller for Tini -fasen, og 77% eller for Tini -fasen₃.

Merk at det røde punktet er nærmere Tini -fasen₃ den fra Tini -fasen. Dette betyr at det må være mer tini₃ den tini; Og derfor avstanden eller spakarmen som tilsvarer tini₃ Det må være det lengste, det motsatte (70%-58%).

Når vi vet dette, fortsetter vi å beregne F ^Tini3:

F ^Tini3 = (70% - 58%) / (77% - 58%)

= 0.6316 eller 63.16%

Faktisk 63.16% av legeringen tilsvarer Tini -fasen₃. I mellomtiden tilsvarer Tini -fasen:

1 = F ^Tini3 + F ^Tini

F ^Tini = 1 - F ^Tini3

= 0.3684 eller 36.84%

Avslutningsvis på øvelsene som er hevet, kan vi si at spakregelen er veldig nyttig for å bestemme brøkene i hver fase i likevekt for et to -komponentsystem.

Referanser

1. Walter J. Moore. (1963). Fysisk kjemi. I kjemisk kinetikk. Fjerde utgave, Longmans.
2. Iran. Levine. (2009). Prinsipper for fysikjemi. Sjette utgave. Mc Graw Hill.
3. Wikipedia. (2020). Spakregel. Hentet fra: i.Wikipedia.org
4. Michael Adewumi. (18. mai 2020). Spakregelen. Gjenopprettet fra: Eng.Librettexts.org
5. Adam Warren. (1997). Fasediagrammer: binde linjer og spakregelen. Gjenopprettet fra: Southampton.Ac.Storbritannia
6. University of Cambridge. (2020). Spakregelen. Hentet fra: Doitpoms.Ac.Storbritannia